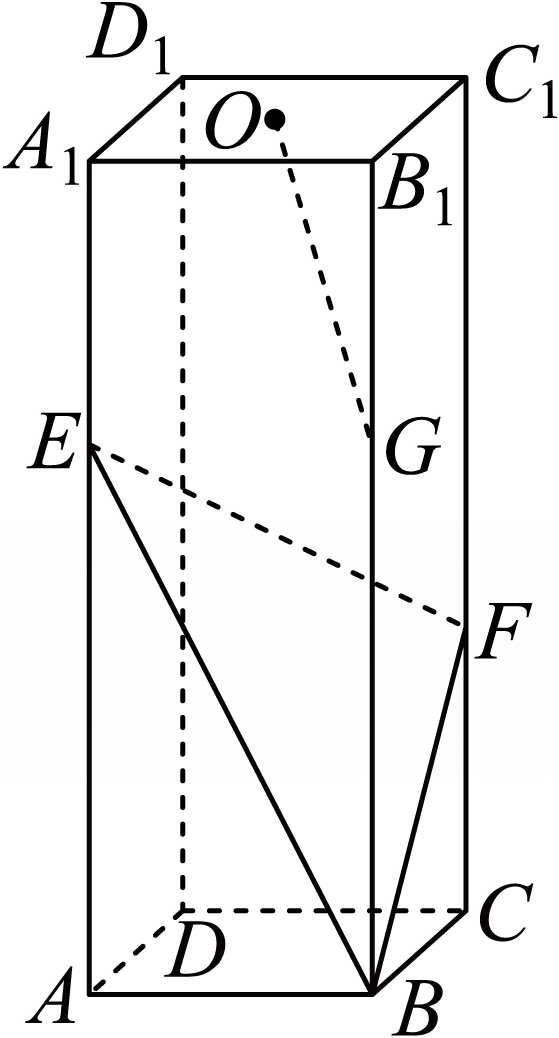
如图，在直四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$中，底面$ABCD$是边长为$2$的正方形，侧棱$DD_{1}=6$，点$E$、$F$分别在侧棱$AA_{1}$、$CC_{1}$上，且$A_{1}E=CF=2$．

$(1)$求平面$BEF$与平面$ABCD$夹角的余弦值；

$(2)$已知$O$为底面$A_{1}B_{1}C_{1}D_{1}$的中心，在$BB_{1}$上是否存在点$G$，使得$OG//$平面$BEF$？若存在，求出$\dfrac{BG}{B{B}_{1}}$；若不存在，请说明理由．

$(1)$$\\dfrac{\\sqrt{6}}{6}$；

$(2)$存在，且$\\dfrac{BG}{B{B}_{1}}=\\dfrac{1}{2}$

$(1)$

$\because $ 在直四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$中，底面$ABCD$是边长为$2$的正方形，

以点$D$为原点，$DA$、$DC$、$DD_{1}$所在直线分别为$x$、$y$、$z$轴，建立如图所示的空间直角坐标系，

则$A(2,0,0)$、$B(2,2,0)$、$E(2,0,4)$、$F(0,2,2)$，

$\therefore \overrightarrow{AB}=(0,2,0)$，$\overrightarrow{BE}=(0,-2,4)$，$\overrightarrow{EF}=(-2,2,-2)$，

设平面$BEF$的法向量为$\boldsymbol{m}=(x,y,z)$，

则$\begin{cases}\boldsymbol{m}\cdot \overrightarrow{BE}=-2y+4z=0\\ \boldsymbol{m}\cdot \overrightarrow{EF}=-2x+2y-2z=0\end{cases}$，

令$x=1$，则$\boldsymbol{m}=(1,2,1)$，

易知$\boldsymbol{n}=(0,0,1)$是平面$ABCD$的一个法向量，

$\therefore \vert \cos \langle \boldsymbol{m},\boldsymbol{n}\rangle \vert =\dfrac{\vert \boldsymbol{m}\cdot \boldsymbol{n}\vert }{\vert \boldsymbol{m}\vert \cdot \vert \boldsymbol{n}\vert }=\dfrac{1}{\sqrt{6}}=\dfrac{\sqrt{6}}{6}$，

即平面$BEF$与平面$ABCD$夹角的余弦值为$\dfrac{\sqrt{6}}{6}$．

$(2)$由$(1)$可得$O(1,1,6)$、$B_{1}(2,2,6)$，$\overrightarrow{B{B}_{1}}=(0,0,6)$，

假设存在满足条件的点$G$，设$G(2,2,t)(0\leqslant t\leqslant 6)$，

$\therefore \overrightarrow{OG}=(1,1,t-6)$，

$\because OG//$平面$BEF$，

$\therefore \boldsymbol{m}\cdot \overrightarrow{OG}=1+2+t-6=t-3=0$，

解得$t=3$，

故当$\dfrac{BG}{B{B}_{1}}=\dfrac{1}{2}$时，$OG//$平面$BEF$．