如图，在多面体$ABCDEFGH$中，平面$ABCD$与平面$EFGH$均为矩形且相互平行，$AB=1$，$BC=3$，$EF=2$，$FG=4$，$AE=DH$，$BF=CG$，$AH\bot EF$.设$\angle DHE=\theta $.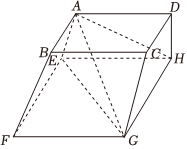
$(1)$求证：平面$AEHD\bot $平面$EFGH$；
$(2)$若多面体$ABCDEFGH$的体积为$\dfrac{8}{3}$：
$($ⅰ）求$\theta $；
$($ⅱ）求平面$AEF$与平面$AEG$夹角的余弦值.

$(1)$ 证明见解析
$(2)$ $(ⅰ)$ $\\dfrac{\\pi }{4}$
$(ⅱ)$ $\\dfrac{\\sqrt{3}}{3}$

$(1)$证明：因为四边形$EFGH$是矩形，所以$EF\bot EH$，
又因为$EF\bot AH$，$EH\cap AH=H$，$EH$，$AH\subset $平面$AEHD$，
所以$EF\bot $平面$AEHD$，又$EF\subset $平面$EFGH$，
所以平面$AEHD\bot $平面$EFGH$；
$(2)\left(i\right) $因为$AE=DH$，所以四边形$ADHE$是等腰梯形，如图，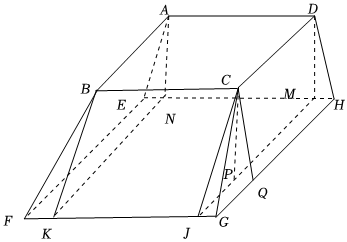
，
过点$D$作$DM\bot EH$，垂足为$M$，过点$A$作$AN\bot EH$，垂足为$N$，
则$HM=EN=\dfrac{1}{2}\left(EH-AD\right)=\dfrac{1}{2}$，同理，作$CJ\bot FG$，$BK\bot FG$，则$FK=JG=\dfrac{1}{2}$，
因为平面$AEHD\bot $平面$EFGH$，平面$AEHD\cap $平面$EFGH=EH$，
所以$DM\bot $平面$EFGH$，$AN\bot $平面$EFGH$，记$DM=AN=h$，
连接$MJ$，$NK$，作$CP\bot MJ$，则$CP=DM=h$，
由对称性可知$V_{BFK-AEN}=V_{CJG-DMH}$，所以$V_{ABCDEFGH}=V_{BCJK-ADMN}+2V_{CJG-DMH}$，
$V_{BCJK-ADMN}=S_{四边形CDMJ}×MN=\dfrac{1}{2}\left(1+2\right)h×3=\dfrac{9}{2}h$，
$V_{CJG-DMH}=V_{CPQ-DMH}+V_{CCPQJG}=\left(\dfrac{1}{2}×\dfrac{1}{2}×h\right)×1+\dfrac{1}{3}\left(\dfrac{1}{2}×1\right)×h=\dfrac{5}{12}h$，
所以$V_{ABCDEFGH}=\dfrac{9}{2}h+2×\dfrac{5}{12}h=\dfrac{16}{3}h=\dfrac{8}{3}$，所以$h=\dfrac{1}{2}$，
在$Rt\triangle DHM$中，$DM=h=\dfrac{1}{2},HM=\dfrac{1}{2}$，
所以$\theta =∠DHE=\dfrac{\pi }{4}$；
$\left(ii\right)$由（ⅰ）以$N$为原点，以$NK$，$NH$，$NA$所在直线分别为$x$，$y$，$z$轴建立如图所示的空间直角坐标系，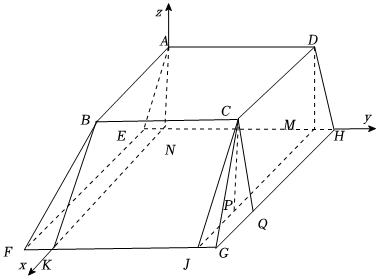
，
则$A\left(0,0,\dfrac{1}{2}\right),E\left(0,-\dfrac{1}{2},0\right),F\left(2,-2,0\right)$，$G\left(2,\dfrac{7}{2},0\right)$，
则$\overrightarrow{AE}=\left(0,-\dfrac{1}{2},-\dfrac{1}{2}\right),\overrightarrow{EF}=\left(2,0,0\right),\overrightarrow{EG}=\left(2,4,0\right)$，
设平面$AEF$的法向量$\overrightarrow{n_1}=\left(x_1,y_1,z_1\right)$，
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}\cdot \overrightarrow{AE}=0}\\{\overrightarrow{EF}\cdot \overrightarrow{{n}_{1}}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{-\dfrac{1}{2}{y}_{1}-\dfrac{1}{2}{z}_{1}=0}\\{2{x}_{1}=0}\end{array}\right.$，令$y_{1}=1$，则$z_{1}=-1,x_{1}=0$，所以$\overrightarrow{{n}_{1}}=\left(0,1,-1\right)$，
设平面$AEG$的法向量$\overrightarrow{n_2}=\left(a,b,c\right)$，
则$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}\cdot \overrightarrow{AE}=0}\\{\overrightarrow{EG}\cdot \overrightarrow{{n}_{2}}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{-\dfrac{1}{2}b-\dfrac{1}{2}c=0}\\{2a+4b=0}\end{array}\right.$，令$a=2$，则$b=-1$，$c=1$，所以$\boldsymbol{n_2}=\left(2,-1,1\right)$，
所以$\cos⟨\overrightarrow{n_{1}},\overrightarrow{n_{2}}⟩=\dfrac{\overrightarrow{n_{1}}\cdot\overrightarrow{n_{2}}}{|\overrightarrow{n_{1}}||\overrightarrow{n_{2}}|}=\dfrac{-2}{\sqrt{2}\times\sqrt{6}}=-\dfrac{\sqrt{3}}{3}$，
设平面$AEF$与平面$AEG$夹角为$\alpha $，则$\cos\alpha=|\cos⟨\overrightarrow{n_{1}},\overrightarrow{n_{2}}⟩|=\dfrac{\sqrt{3}}{3}$，
所以平面$AEF$与平面$AEG$夹角的余弦值为$\dfrac{\sqrt{3}}{3}$.