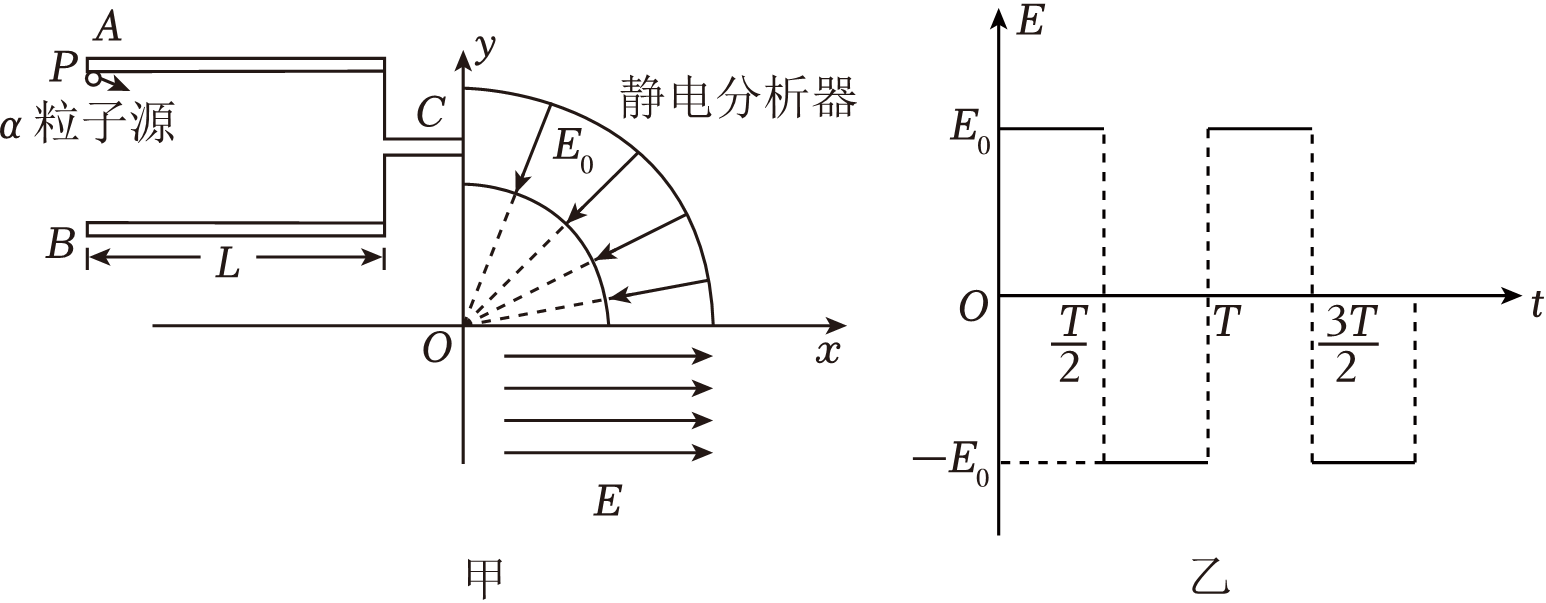
如图甲所示，在空间坐标系$xOy$中，$\alpha$射线管放置在第Ⅱ象限，由平行金属板$A$、$B$和平行于金属板的细管$C$组成，细管$C$到两金属板距离相等，右侧的开口在$y$轴上，金属板和细管$C$均平行于$x$轴。放射源$P$在$A$板左端，可以沿特定方向发射某一初速度的$\alpha$粒子。若金属板长为$L$、间距为$d$，当$A$、$B$板间加上某一电压时，$\alpha$粒子刚好能以速度$v_{0}$从细管$C$水平射出，进入位于第$I$象限的静电分析器中。静电分析器中存在着辐向电场，分布在整个第$I$象限的区域内，电场线沿半径方向，指向与坐标系原点重合的圆心$O$。粒子在该电场中恰好做匀速圆周运动，$\alpha$粒子运动轨迹处的场强大小为$E_{0}$。$t=0$时刻$\alpha$粒子垂直$x$轴进入第$IV$象限的交变电场中，交变电场的场强大小为$E_{0}$，方向随时间的变化关系如图乙所示，规定沿$x$轴正方向为电场的正方向。已知$\alpha$粒子的电荷量为$2e$（$e$为元电荷）、质量为$m$，重力不计。以下说法中正确的是$(\qquad)$

$\\alpha$粒子从放射源$P$运动到$C$的过程中动能减少了$\\dfrac{md^{2}v_{0}^{2}}{L^{2}}$

$\\alpha$粒子从放射源$P$发射时的速度大小为$v_{0}\\sqrt{1 + \\dfrac{d^{2}}{L^{2}}}$

$\\alpha$粒子在静电分析器中运动的轨迹半径为$\\dfrac{mv_{0}^{2}}{eE_{0}}$

在$t=2T$时刻，$\\alpha$粒子的坐标为$(\\dfrac{mv_{0}^{2}}{2eE_{0}} + \\dfrac{eE_{0}T^{2}}{m}, - 2\\nu_{0}T)$

$\rm AB$、设$\alpha$粒子运动到$C$处时速度为$v_{0}$。$\alpha$粒子从放射源$P$运动到$C$的逆运动为类平抛运动，水平方向有：$L=v_{0}t$

竖直方向有：$\dfrac{d}{2} = \dfrac{1}{2}at^{2}$

由牛顿第二定律有：$2e\dfrac{U}{d} = ma$

联立解得：$U = \dfrac{md^{2}v_{0}^{2}}{2eL^{2}}$

$\alpha$粒子从放射源发射出到$C$的过程，由动能定理有

$﹣2e\cdot $$\dfrac{1}{2}$$U=\Delta E_{k}$

解得：$\Delta E_{k} = - eU = - \dfrac{md^{2}v_{0}^{2}}{2L^{2}}$，即$\alpha$粒子从放射源$P$运动到$C$的过程中动能减少了$\dfrac{md^{2}v_{0}^{2}}{2L^{2}}$

设$\alpha$粒子发射时速度的大小为$v$。$\alpha$粒子从放射源发射至运动到$C$的过程，由动能定理有

$- \dfrac{1}{2} \times 2$$eU$$= \dfrac{1}{2}mv_{0}^{2} - \dfrac{1}{2}mv^{2}$

解得：$v = v_{0}\sqrt{1 + \dfrac{d^{2}}{L^{2}}}$，故$\rm A$错误，$\rm B$正确；

$\rm C$、$\alpha$粒子进入静电分析器中，由静电力提供向心力，由牛顿第二定律有$2eE_{0} = m\dfrac{v_{0}^{2}}{r}$

解得$\alpha$粒子在静电分析器中运动的轨迹半径为：$r = \dfrac{mv_{0}^{2}}{2eE_{0}}$，故$\rm C$错误；

$\rm D$、$\alpha$粒子垂直$x$轴进入第$IV$象限的交变电场中，$t$$= \dfrac{T}{2}$时，$\alpha$粒子沿$x$方向的速度为

$v_{x}$$= \dfrac{2eE_{0}}{m}$$\cdot $$\dfrac{T}{2}$

所以一个周期内，$\alpha$粒子在$x$方向的平均速度为$\overline{v_{x}} = \dfrac{v_{x}}{2} = \dfrac{eE_{0}T}{2m}$

每个周期$\alpha$粒子在$x$正方向前进距离为$x_{0} = \overline{v_{x}}T = \dfrac{eE_{0}T^{2}}{2m}$

因为开始计时时$\alpha$粒子横坐标为$r = \dfrac{mv_{0}^{2}}{2eE_{0}}$

所以$t=2T$时，$\alpha$粒子的横坐标为$x = r + 2x_{0} = \dfrac{mv_{0}^{2}}{2eE_{0}} + 2 \times \dfrac{eE_{0}T^{2}}{2m}$

$\alpha$粒子的纵坐标为

$y=﹣v_{0}\cdot 2T$

在$nT$时$\alpha$粒子的坐标为：$(\dfrac{mv_{0}^{2}}{2eE_{0}} + \dfrac{eE_{0}T^{2}}{m}, - 2v_{0}T)$，故$\rm D$正确。

故选：$\rm BD$。