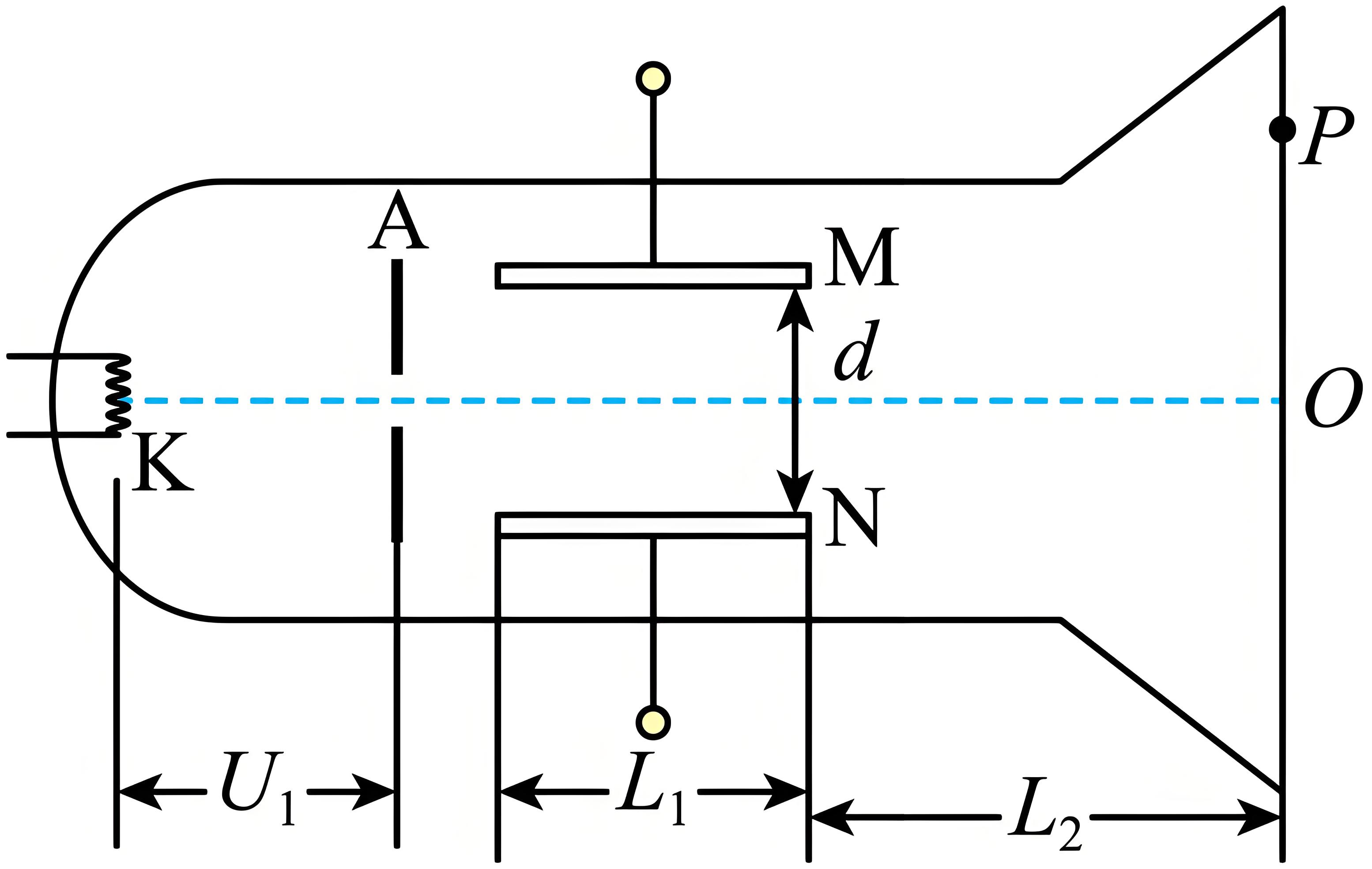
电子穿过$A$板时速度大小$v_{0}$；

$\\sqrt{\\dfrac{2eU_{1}}{m}}$

电子穿过加速电场的过程，由动能定理得$eU_{1}=\dfrac{1}{2}mv_{0}^{2}-0$

解得$v_{0}=\sqrt{\dfrac{2eU_{1}}{m}}$

电子从偏转电场射出时的位移侧移量$y$；

$\\dfrac{U_{2}L_{1}^{2}}{4U_{1}d}$

电子在偏转电场中做类平抛运动，垂直于电场方向做匀速直线运动，则有$L_{1}=v_{0}t$

沿电场方向做初速度为零的匀加速直线运动，有$y=\dfrac{1}{2}at^{2}$

根据牛顿第二定律得$e\dfrac{U_{2}}{d}=ma$

联立解得电子在偏转电场中侧移量为$y=\dfrac{U_{2}L_{1}^{2}}{4U_{1}d}$

$P$点到$O$点的距离。

$\\dfrac{U_{2}L_{1}\\left( L_{1}+2L_{2} \\right)}{4dU_{1}}$

方法一：电子离开偏转电场时在竖直方向的速度$v_{y}=at_{1}$

电子离开偏转电场后做匀速直线运动，电子在水平方向的分速度为$v_{0}$保持不变，运动时间$t_{2}=\dfrac{L_{2}}{v_{0}}$

竖直方向产生位移$y_{2}=v_{y}⋅t_{2}$

方程联立解得$y_{2}=\dfrac{U_{2}L_{1}L_{2}}{2dU_{1}}$

$P$点到$O$点的距离$y=y_{1}+y_{2}=\dfrac{U_{2}L_{1}^{2}}{4dU_{1}}+\dfrac{U_{2}L_{1}L_{2}}{2dU_{1}}=\dfrac{U_{2}L_{1}\left( L_{1}+2L_{2} \right)}{4dU_{1}}$

方法二：利用末速度反向延长线过水平位移中点，利用三角形相似可得

$\dfrac{y}{y_{OP}}=\dfrac{\dfrac{L_{1}}{2}}{\dfrac{L_{1}}{2}+L_{2}}=\dfrac{L_{1}}{L_{1}+2L_{2}}$，$y_{OP}=\dfrac{U_{2}L_{1}\left( L_{1}+2L_{2} \right)}{4dU_{1}}$