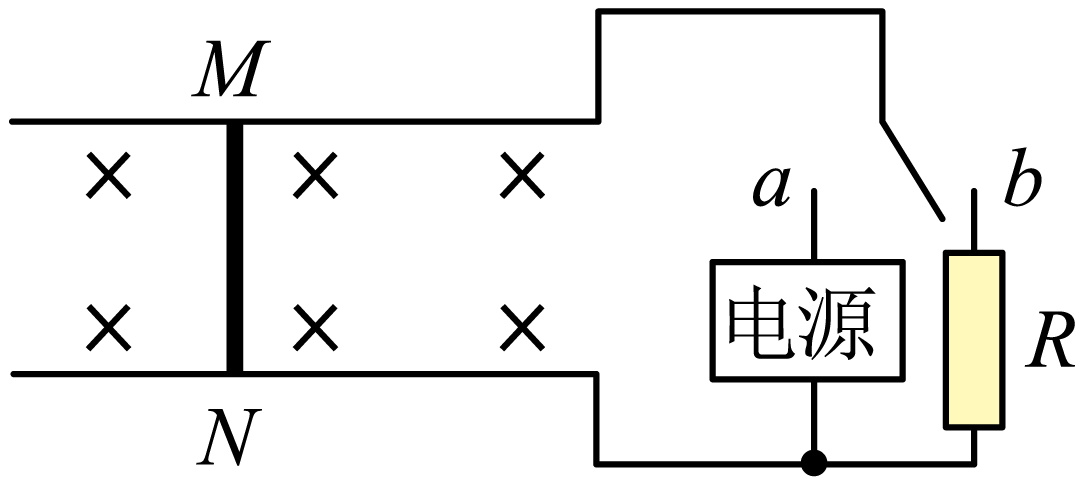
若开关$\rm S$接$a$，当棒中电流由$M$流向$N$时，棒的加速度的大小和方向是怎样的；

$2\\;\\rm m/s^{2}$，方向向右；

当电流从$M$流向$N$时，由左手定则可判断安培力向右，故加速度方向向右。根据牛顿第二定律有$BIL=ma$

代入数据可得$a=2\;\rm m/s^{2}$

若开关$\rm S$始终接$a$，使棒由静止开始在最短时间内向左移动$8m$后而停下，求此过程棒的最大速度是多少；

$4\\;\\rm m/s$；

开关始终接$a$时，要想在最短时间内使棒向左移动$8m$而静止，则棒先向左做匀加速直线运动，再向左做匀减速直线运动，且加速度大小不变，只是方向改变。根据对称性可知加速过程中位移大小为$x=4m$

又因为有$x=\dfrac{v^{2}}{2a}$

联立解得$v=4\;\rm m/s$

要想棒由静止开始在最短时间内向左移动$14\;\rm m$后停下，求此过程棒中产生的焦耳热是多少。

$1.6\\;\\rm J$

先接$a$一段时间$t_{1}$，电流由$N$到$M$，再接到$b$端一段时间$t_{2}$，再接到$a$端一段时间$t_{3}$，电流由$M$到$N$，最后接到$b$静止。第一段，则有

$v=at_{1}x_{1}=\dfrac{1}{2}at_{1}{}^{2}$

$Q_{1}=I^{2}rt_{1}$

第二段，则有由动量定理$- B\overline{I}Lt_{2}=mv'-mv$

且$\overline{I}t_{2}=\dfrac{BLx_{2}}{R+r}$

则有$Q_{2}=\left( \dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv'^{2} \right)\dfrac{r}{R+r}$

第二段末的加速度与第三段相同，则第三段$\dfrac{B^{2}L^{2}v'}{R+r}=ma$

$v'=a_{3}t$

$x_{3}=\dfrac{1}{2}a{t_{3}}^{2}$

$Q_{3}=I^{2}rt_{3}$

又$x_{1}+x_{2}+x_{3}=7$

解得$v'=6\;\rm m/s$

$t_{1}=3\;\rm s$

$t_{3}=1\;\rm s$

故$Q=1.6\;\rm J$