高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
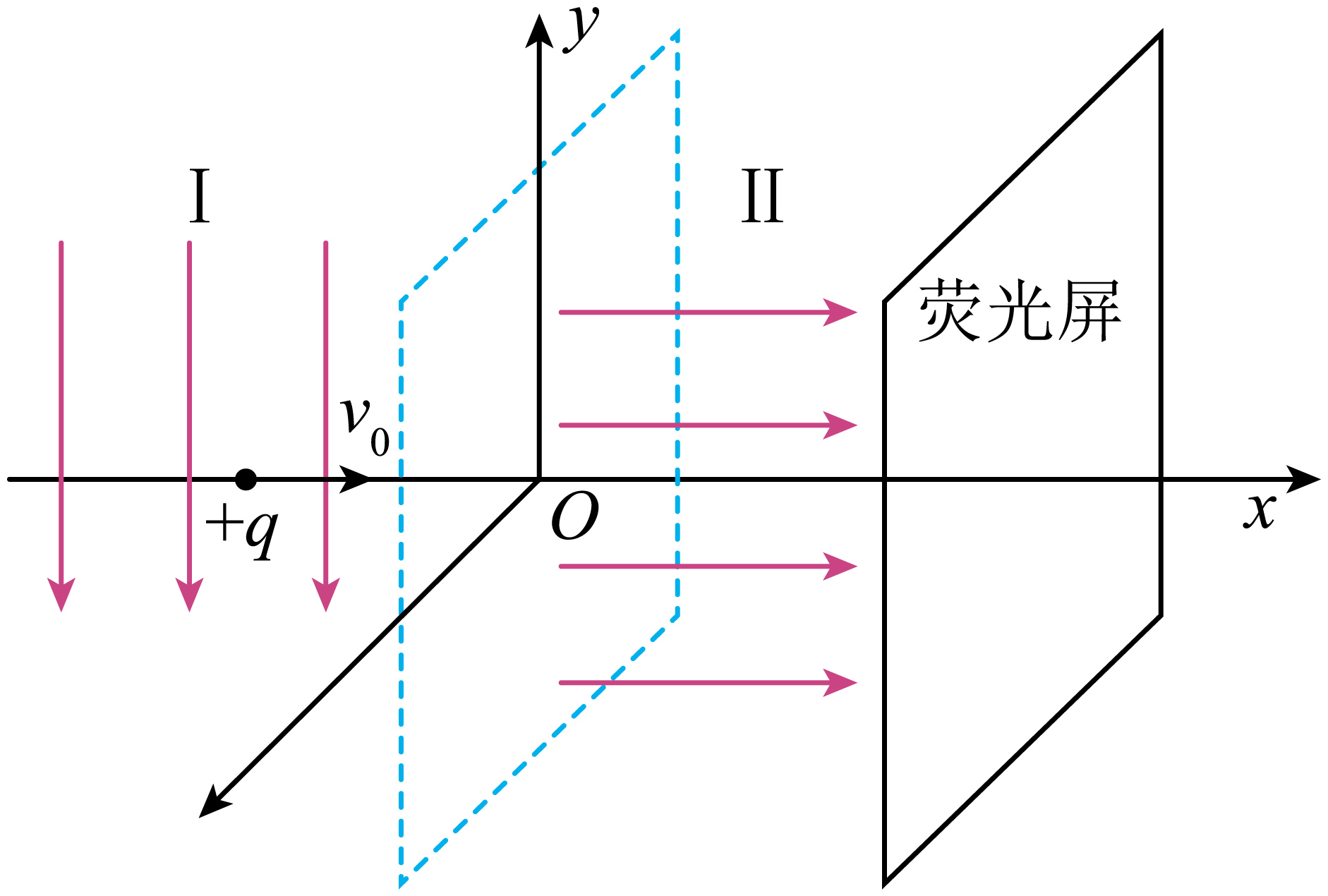
如图所示的三维空间中,$yOz$平面左侧区域记为Ⅰ,区域Ⅰ内存在沿$y$轴负方向的匀强电场;$yOz$平面与垂直于$x$轴足够大的荧光屏之间的区域记为Ⅱ,区域Ⅱ内存在沿$x$轴正方向的匀强磁场,磁感应强度大小为$B$,荧光屏与$x$轴交点位置的坐标不确定。一质量为$m$、电荷量为$+q$的粒子从坐标$(-L,0,0)$处进入区域Ⅰ,粒子初速度大小为$v_{0}$,方向沿着$x$轴正方向,经过$yOz$平面时的坐标为$(0,-L,0)$,再经过磁场偏转后击中荧光屏,不计粒子的重力。
求粒子经过$yOz$平面时沿$y$轴的速度大小$v_{y}$。
$2v_{0}$
"]]粒子在区域Ⅰ内,在$x$轴方向做匀速直线运动,可得粒子在区域Ⅰ内的时间为$t_{1}=\dfrac{L}{v_{0}}$
因受到电场力的作用,粒子在区域Ⅰ内时,在$y$轴上做匀加速运动
可得$L=\dfrac{1}{2}a_{1}t_{1}^{2}$
解得$a_{1}=\dfrac{2v_{0}^{2}}{L}$
则可得粒子经过$yOz$平面时沿$y$轴的速度大小$v_{y}=a_{1}t_{1}=2v_{0}$
若荧光屏与$x$轴交点的$x$轴坐标为$\dfrac{3\pi mv_{0}}{qB}$,求粒子在磁场中的运动时间$t$。
$\\dfrac{3\\pi m}{qB}$
"]]因在区域Ⅱ内的磁场方向沿$x$轴正方向,则将粒子进入区域Ⅱ内的速度分解为沿$x$轴方向和垂直于$x$轴方向,沿$x$轴方向的速度大小为$v_{0}$,垂直于$x$轴方向的速度大小为$2v_{0}$,沿$y$轴负方向,则可得粒子在磁场中的运动时间为$t=\dfrac{\dfrac{3\pi mv_{0}}{qB}}{v_{0}}=\dfrac{3\pi m}{qB}$
若粒子击中荧光屏时$z$轴坐标为$\dfrac{mv_{0}}{qB}$,求荧光屏与$x$轴交点的$x$坐标。
$\\left( n+\\dfrac{1}{6} \\right)\\dfrac{2\\pi mv_{0}}{Bq}(n=0,1,2,3,\\cdots)$或$\\left( n-\\dfrac{1}{6} \\right)\\dfrac{2\\pi mv_{0}}{Bq}(n=1,2,3,\\cdots)$
"]]根据洛伦兹力提供向心力,可得$m\dfrac{(2v_{0})^{2}}{R}=Bq·2v_{0}$
解得$R=\dfrac{2mv_{0}}{Bq}$
已知粒子击中荧光屏时$z$轴坐标为$\dfrac{mv_{0}}{qB}$,即在$z$轴方向上的位移为$d=\dfrac{mv_{0}}{Bq}$
设粒子在$yOz$平面上的速度偏转的角度为$\theta$,则可得$\cos\theta=\dfrac{R-d}{R}=\dfrac{1}{2}$
解得$\theta=2n\pi+\dfrac{\pi}{3}(n=0,1,2,3,\cdots)$
或$\theta=2n\pi-\dfrac{\pi}{3}(n=1,2,3,\cdots)$
可知粒子在磁场中运动的周期为$T=\dfrac{2\pi m}{qB}$
则粒子在磁场中经历的时间为$t=\dfrac{\theta}{2\pi}T=\left( n+\dfrac{1}{6} \right)\dfrac{2\pi m}{Bq}(n=0,1,2,3,\cdots)$
或$t=\left( n-\dfrac{1}{6} \right)\dfrac{2\pi m}{Bq}(n=1,2,3,\cdots)$
荧光屏与$x$轴交点的$x$坐标为$x=v_{0}t=\left( n+\dfrac{1}{6} \right)\dfrac{2\pi mv_{0}}{Bq}(n=0,1,2,3,\cdots)$
或$x=\left( n-\dfrac{1}{6} \right)\dfrac{2\pi mv_{0}}{Bq}(n=1,2,3,\cdots)$
高中 | 洛伦兹力题目答案及解析(完整版)
