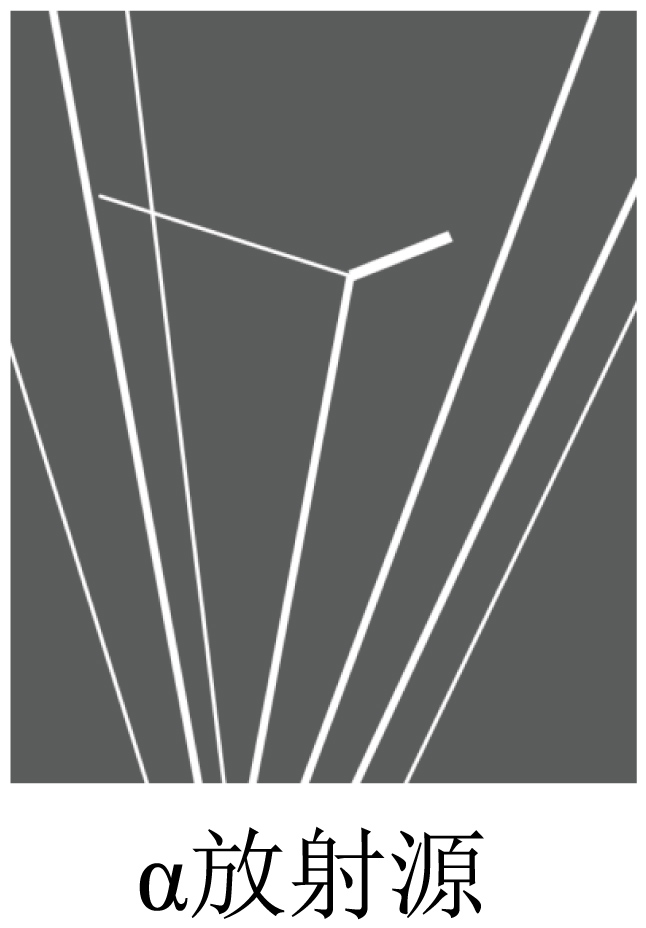
卢瑟福通过$\alpha$粒子轰击氮核实验，最先发现质子，其核反应方程为：$\rm _{7}^{14}N+{_{2}^{4}He}→$                 $++{_{1}^{1}\rm H}$。布拉凯特在充有氮气的云室中重做该实验，拍摄到右图所示的照片。照片显示：在诸多$\alpha$粒子的径迹中有一条发生了分叉，分叉后细而长的是                 的径迹。此后，卢瑟福预言了中子的存在。

根据质量数和电荷数守恒，其核反应方程为$\rm _{7}^{14} N+{_{2}^{4}He}→{_{8}^{17}O}+{_{1}^{1}H}$

布拉凯特在充有氮气的云室中重做该实验，分叉后细而长的是质子的径迹。

$20$世纪$30$年代，德国科学家用$\alpha$粒子轰击铍时产生一种不带电的射线，他们认为是$\gamma$射线。$1932$年约里奥$-$居里夫妇用这种未知射线轰击含氢的石蜡，能打出质子，推算出这种未知射线的能量约为$5.3\;\rm MeV$，与$\alpha$粒子初始能量吻合，也认为这种未知射线是$\gamma$射线。

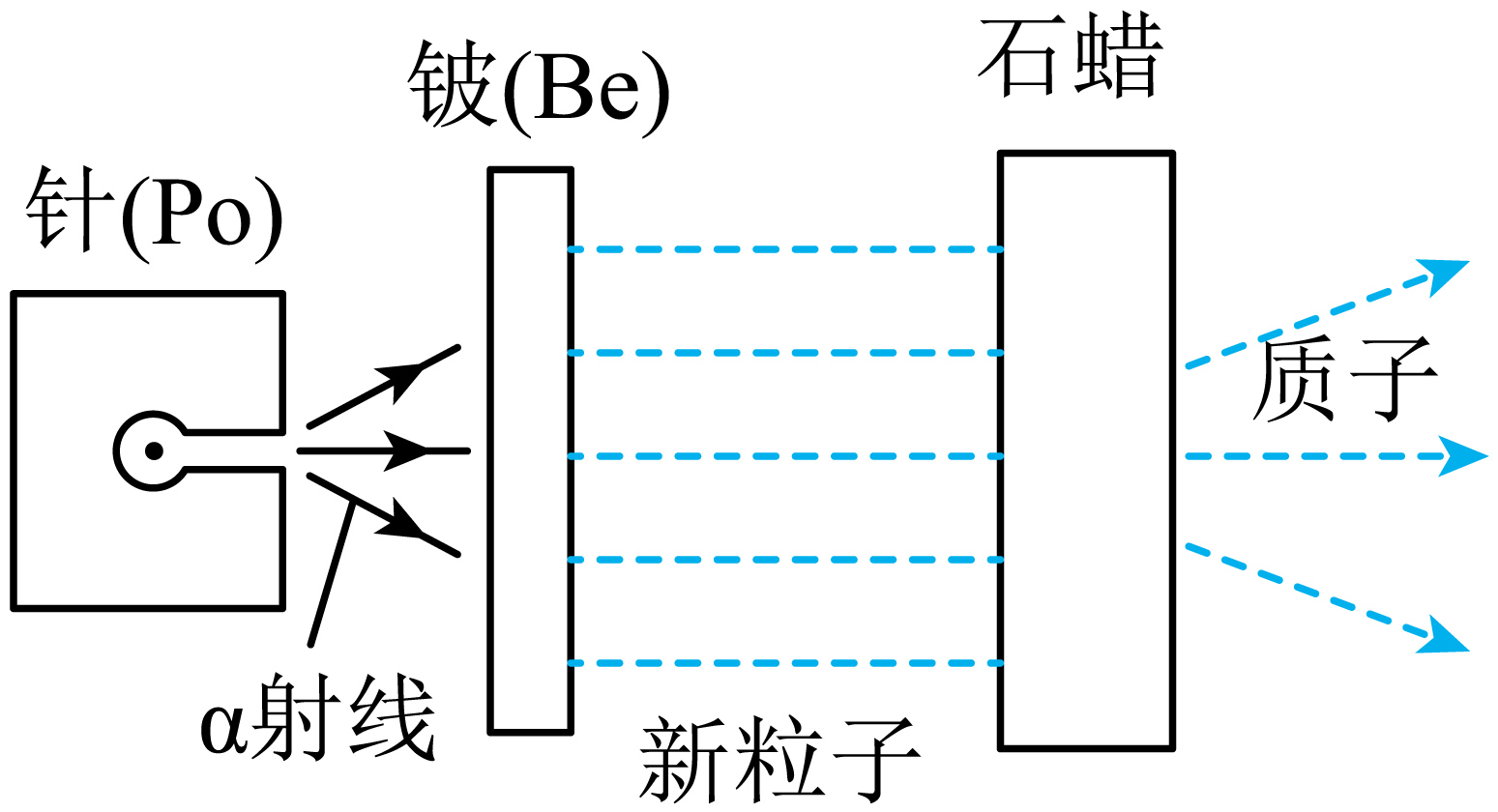
①下列说法正确的是$(\qquad)$

$\rm A$．$\gamma$射线是纵波

$\rm B$．$\gamma$射线是电磁波

$\rm C$．$\alpha$粒子的贯穿本领比$\beta$粒子大

$\rm D$．$\alpha$粒子的电离本领比$\beta$粒子大

②若$\gamma$粒子与静止的质子发生弹性正碰，撞击后$\gamma$粒子消失。请计算碰撞前$\gamma$粒子的能量，并由此说明“未知射线是$\gamma$射线”是否成立？已知质子质量$m_{H}=1.67\times 10^{-27}\;\rm kg$或者$938.3\;\rm MeV/c^{2}$，$\gamma$粒子的动量与其能量关系为$p=\dfrac{E}{c}$，光速$c=3\times 10^{8}\;\rm m/s$；核衰变或核反应中释放出来的$\gamma$粒子能量通常在几十$keV$到几$MeV$之间，最多可达几十$MeV$。

$BD$；未知射线不是$\\gamma$射线，理由见解析

①根据$\gamma$射线的本质可知，$\gamma$射线是电磁波，是横波，$\alpha$粒子的电离本领比$\beta$粒子大，贯穿本领比$\beta$粒子的小，故$\rm BD$正确，$\rm AC$错误。

故选：$\rm BD$。

②设碰撞后质子获得的速度为$v$，$\gamma$粒子与静止的质子发生弹性正碰，由动量守恒定律得$p=\dfrac{E}{c}=m_{\text{H}}v$

由能量守恒定律可知，光子能量转化为质子动能$E_{k}=\dfrac{1}{2}m_{{H}}v^{2}$

两式联立，解出光子的能量$E=2m_{H}c^{2}=2 \times 938.3\;\rm MeV=1876.6\;\rm MeV$

远大于核衰变或核反应释放出的射线的能量，因此未知射线不可能是$\gamma$射线。

查德威克将这种未知粒子与多种原子核碰撞，重做实验，借助质谱仪测量并算出该未知粒子的质量十分接近质子的质量，与卢瑟福“中子”预言吻合。质谱仪的测量原理如图所示，速度选择器的两金属板$M$、$N$间距为$d$，板间区域磁场的磁感应强度大小为$B_{1}$ 。中子与静止的质子发生弹性正碰后，质子由$O$处进入，当板间电压为$U_{0}$时，恰能沿直线经过正下方的$A$孔垂直于磁场方向射入磁感应强度大小为$B_{2}$、垂直纸面向外的匀强磁场中，最后打在照相底片上的$C$点，测出$AC$长度为$L$，元电荷为$e$，不计重力影响。

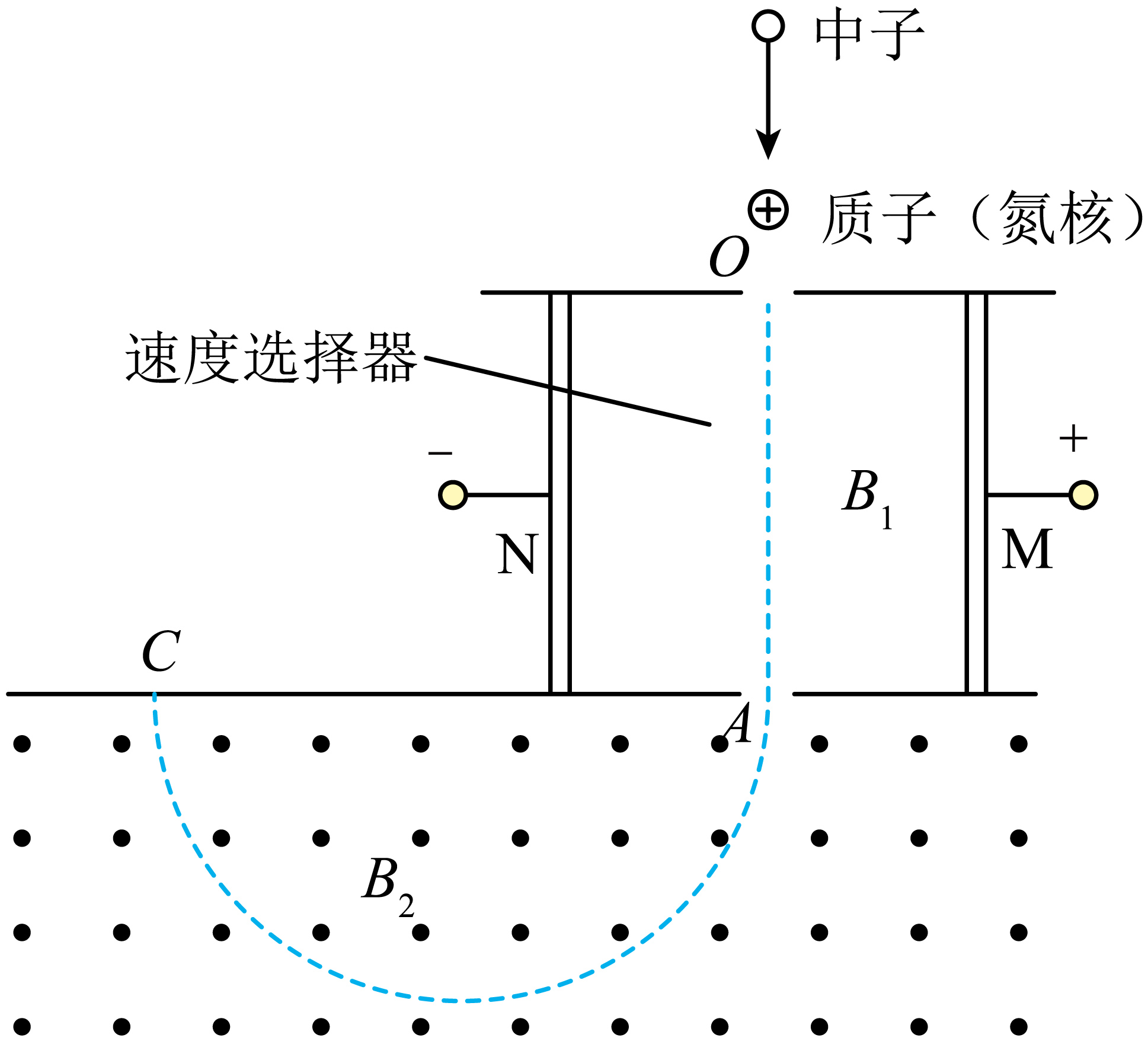
①求质子的质量$m_{H}$（用$B_{1}$、$B_{2}$、$U_{0}$、$d$、$L$、$e$表示）。

②若相同的中子与静止的氮核（$\rm _{7}^{14}N$）发生弹性正碰后，氮核沿$OA$方向进入质谱仪，需将$M$、$N$间电压调为多大时，才能在照相底片上探测到氮核的径迹？（质子、中子的质量均为$u$，结果用$U_{0}$表示）。

①$\\dfrac{edLB_{1}B_{2}}{2U_{0}}$；②$\\dfrac{2}{15}U_{0}$

①速度选择器中，受平衡力$ev_{1}B=eE$

匀强电场中$U_{0}=Ed$

解得$v=\dfrac{U_{0}}{dB_{1}}$

在$B_{2}$磁场中，洛伦兹力提供向心力$evB_{2}=m_{\text{H}}\dfrac{v^{2}}{R}$

且$L=2R$，解得质子的质量$m_{\text{H}}=\dfrac{eLB_{2}}{2v}=\dfrac{edLB_{1}B_{2}}{2U_{0}}$

②设碰撞前中子的速度为$v$，中子与静止的质子发生弹性正碰，遵循动量定律、机械能守恒定律得$m_{1}v=m_{1}v_{1}+m_{2}v_{2}$，$\dfrac{1}{2}m_{1}v^{2}=\dfrac{1}{2}m_{1}{v_{1}}^{2}+\dfrac{1}{2}m_{2}{v_{2}}^{2}$

因质量相等，故$v_{2}=v$

中子与静止的氮核发生弹性正碰，设碰撞后中子的速度为$v_{n}$，氮核的速度为$v_{N}$，规定中子初速度$v$的方向为正方向，由动量守恒定律得$uv=uv_{n}+(14u)v_{N}$

机械能守恒$\dfrac{1}{2}uv^{2}=\dfrac{1}{2}u{v_{n}}^{2}+\dfrac{1}{2} \times (14u){v_{N}}^{2}$

联立解得$v_{\text{N}}=\dfrac{\text{2}}{\text{15}}v$

另一解$v_{N}=0$（舍去）

因带电粒子能沿直线通过速度选择器的速度$v=\dfrac{U}{dB_{1}}$

即选择的速度与电压成正比，故$M$、$M$间电压应调为$U=\dfrac{2}{15}U_{0}$