高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
如图所示,光滑半圆轨道直径沿竖直方向,最低点与水平面相切。对静置于轨道最低点的小球$\rm A$施加水平向左的瞬时冲量$I$,$\rm A$沿轨道运动到最高点时,与用轻绳悬挂的静止小球$\rm B$正碰并粘在一起。已知$I=1.8\rm\;N\cdot s$,$\rm A$、$\rm B$的质量分别为$m_{\rm A}=0.3\rm\;kg$、$m_{\rm B}=0.1\rm\;kg$,轨道半径和绳长均为$R=0.5\rm\;m$,两球均视为质点,轻绳不可伸长,重力加速度$g$取$10\rm\;m/s^{2}$,不计空气阻力。求:
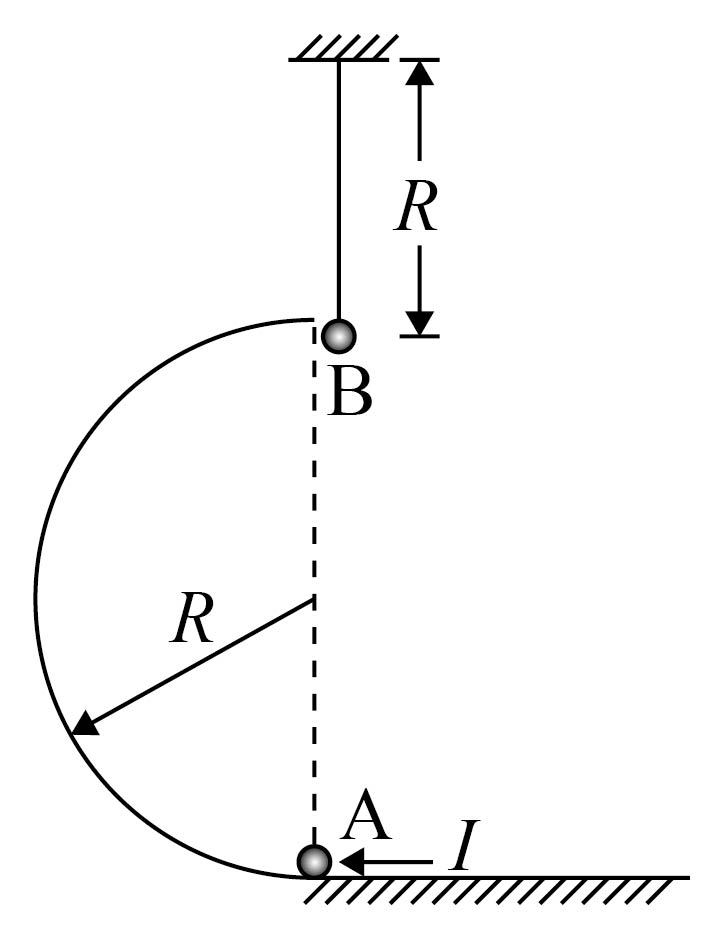
与$\rm B$碰前瞬间$\rm A$的速度大小;
$4$ $\\rm m/s$
"]]根据题意,设小球A从最低点开始运动时的速度为$v_{0}$,由动量定理有$I={{m}_{\text{A}}}{{v}_{0}}$
设与B碰前瞬间A的速度大小$v$,从最低点到最高点,由动能定理有$-mg\cdot2R=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}$
联立代入数据解得$v=4\text{ m}/\text{s}$
$\rm A$、$\rm B$碰后瞬间轻绳的拉力大小。
$11.2$ $\\rm N$
"]]A与用轻绳悬挂的静止小球B正碰并粘在一起,由动量守恒定律有${{m}_{\text{A}}}v=\left( {{m}_{\text{A}}}+{{m}_{\text{B}}} \right){{v}_{}}$
设A、B碰后瞬间轻绳的拉力大小为F,由牛顿第二定律有$F-\left( m_{\text{A}}+m_{\text{B}}\right)g=\left( m_{\text{A}}+m_{\text{B}}\right)\dfrac{v_{}^{2}}{R}$
联立代入数据解得$F=11.2\text{N}$
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
