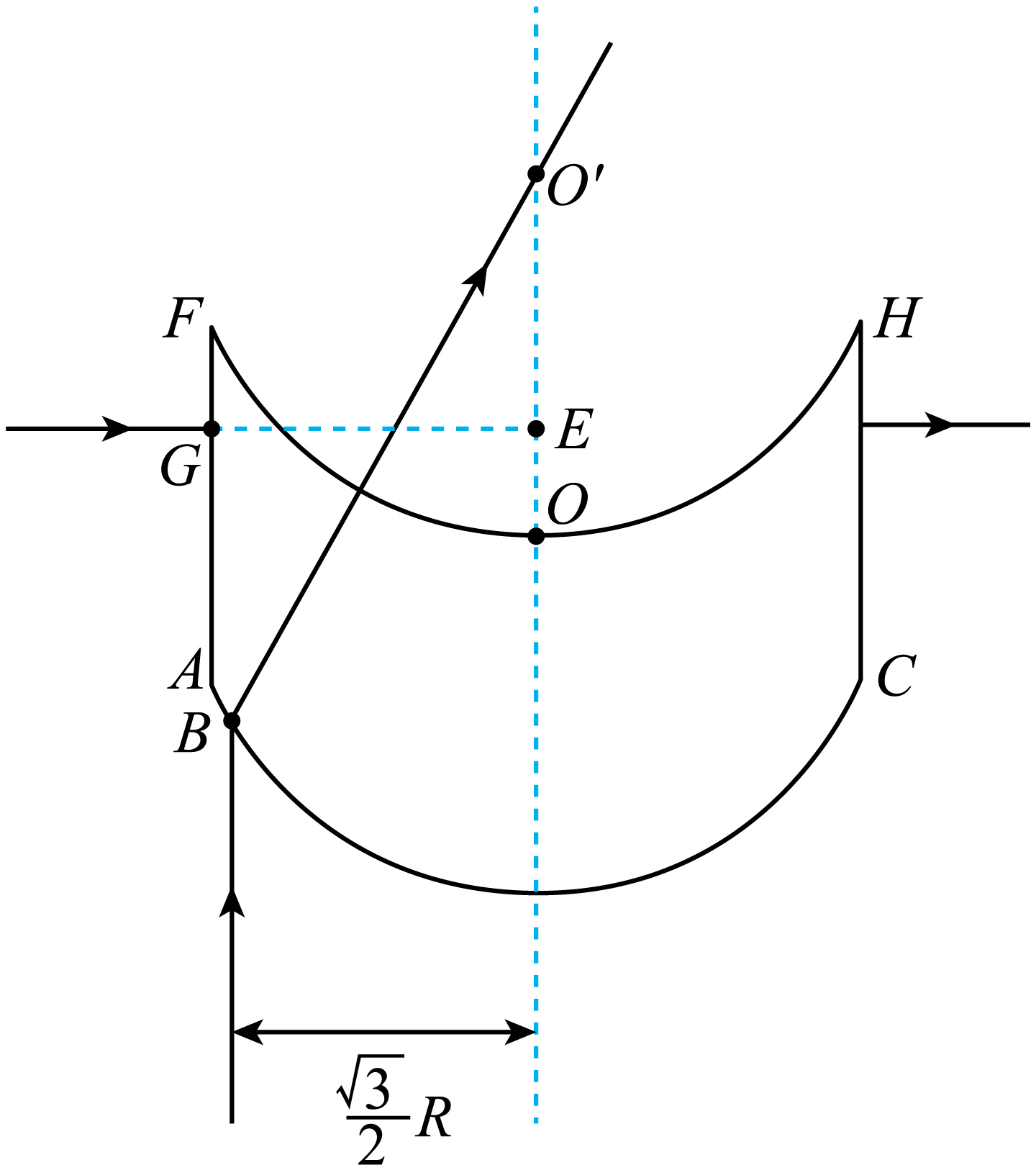
$B$点与$OO'$的距离为$\dfrac{\sqrt{3}}{2}R$，单色光线从$B$点平行于$OO'$射入介质，射出后恰好经过$O'$点，求介质对该单色光的折射率$n$；

$\\sqrt{3}$；

如图

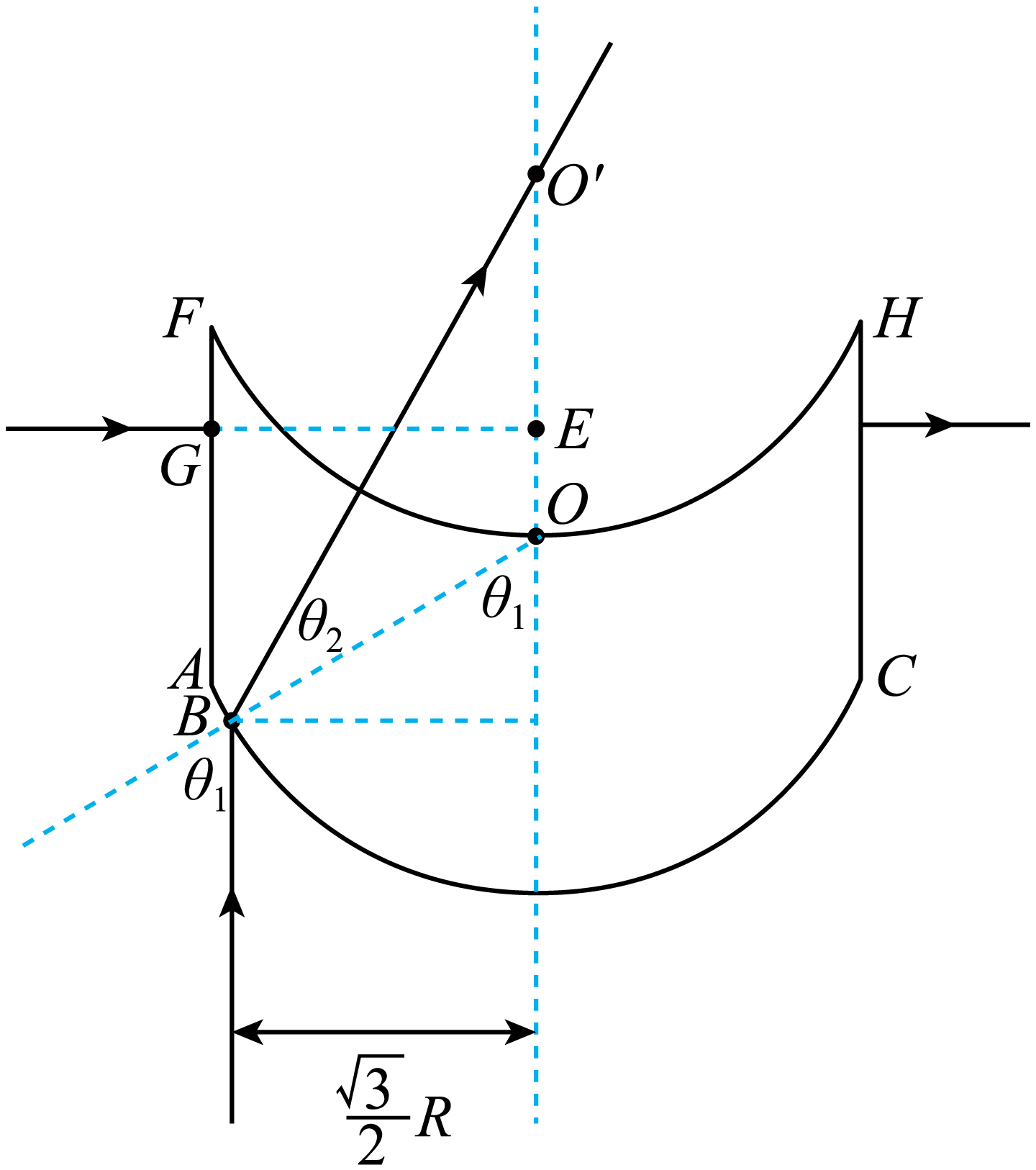
根据题意可知$B$点与$OO'$的距离为$\dfrac{\sqrt{3}}{2}R$，$OB=R$，所以$\sin\theta_{1}=\dfrac{\dfrac{\sqrt{3}}{2}R}{R}=\dfrac{\sqrt{3}}{2}$

可得$\theta_{1}=60^\circ $

又因为出后恰好经过$O'$点，$O'$点为该光学器件上表面圆弧的圆心，则该单色光在上表面垂直入射，光路不变；因为$OB=OO'=R$，所以根据几何关系可知$\theta_{2}=30^\circ $

介质对该单色光的折射率$n=\dfrac{\sin\theta_{1}}{\sin\theta_{2}}=\dfrac{\sin 60^\circ}{\sin 30^\circ}=\sqrt{3}$；

若该单色光线从$G$点沿$GE$方向垂直$AF$射入介质，并垂直$CH$射出，出射点在$GE$的延长线上，$E$点在$OO'$上，$O'$、$E$两点间的距离为$\dfrac{\sqrt{2}}{2}R$，空气中的光速为$c$，求该光在介质中的传播时间$t$。

$\\dfrac{19\\sqrt{3}R}{5c}$。

若该单色光线从$G$点沿$GE$方向垂直$AF$射入介质，第一次射出介质的点为$D$，且$O'E=\dfrac{\sqrt{2}}{2}R$，可知$\sin\theta=\dfrac{\dfrac{\sqrt{2}}{2}R}{R}= \dfrac{\sqrt{2}}{2}$

由于$\sin\theta=\dfrac{\sqrt{2}}{2} \gt \sin C=\dfrac{1}{n}=\dfrac{\sqrt{3}}{3}$

所以光线在上表面$D$点发生全反射，轨迹如图

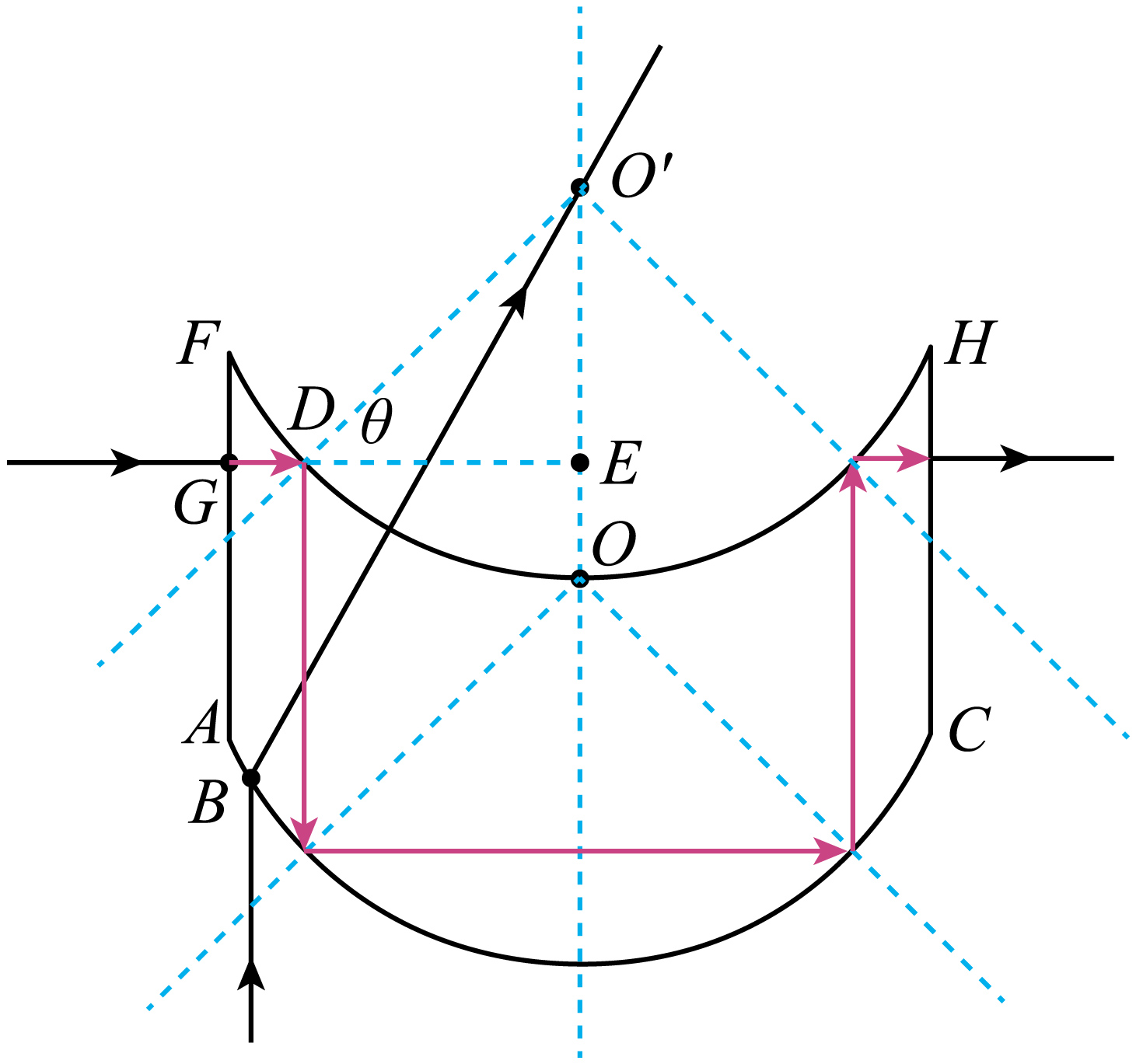
根据几何关系有则光在介质中传播的距离为$L=2(GE+AF)=\dfrac{19}{5}R$

光在介质中传播的速度为$v=\dfrac{c}{n}=\dfrac{\sqrt{3}c}{3}$

所以光在介质中的传播时间$t=\dfrac{L}{v}=\dfrac{\dfrac{19}{5}R}{\dfrac{\sqrt{3}c}{3}}=\dfrac{19\sqrt{3}R}{5c}$。