高中 | 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
高中 | 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
某同步加速器简化模型如图所示,其中仅直通道$PQ$内有加速电场,三段圆弧内均有可调的匀强偏转磁场$B$。带电荷量为$−q$、质量为$m$的离子以初速度$v_{0}$从$P$处进入加速电场后,沿顺时针方向在加速器内循环加速。已知加速电压为$U$,磁场区域中离子的偏转半径均为$R$。忽略离子重力和相对论效应,下列说法正确的是$(\qquad)$
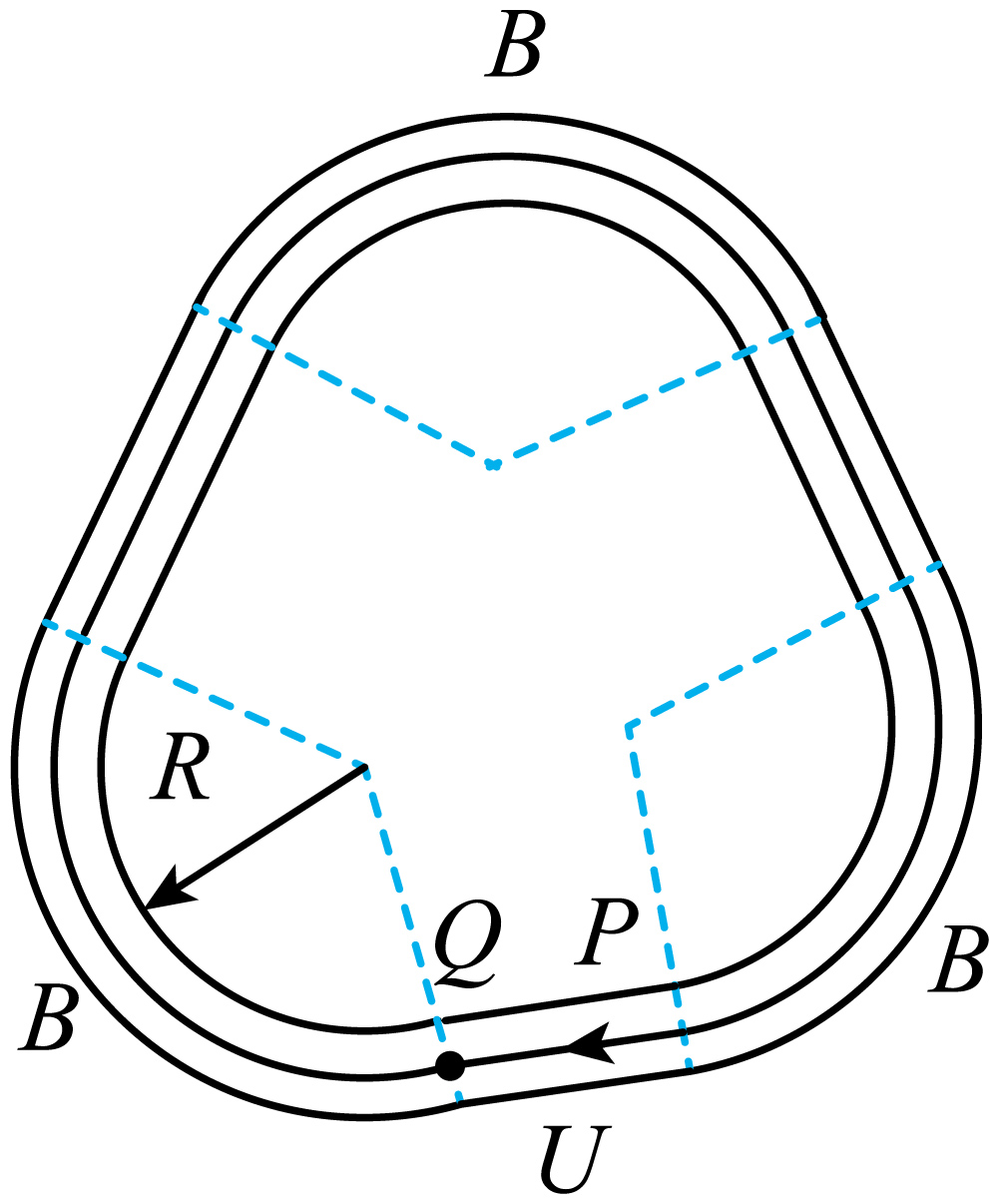
偏转磁场的方向垂直纸面向里
","第$1$次加速后,离子的动能增加了$2qU$
","第$k$次加速后。离子的速度大小变为$\\dfrac{\\sqrt{m^{2}v_{0}^{2}+kqUm}}{m}$
","第$k$次加速后,偏转磁场的磁感应强度大小应为$\\dfrac{\\sqrt{m^{2}v_{0}^{2}-2kqUm}}{qR}$
"]$\rm A$.直线通道$PQ$有电势差为$U$的加速电场,粒子带负电,粒子沿顺时针方向运动,由左手定则可知,偏转磁场的磁感应强度方向垂直纸面向里,故$\rm A$正确;
$\rm BC$.根据题意,由动能定理可知,加速一次后,带电粒子的动能增量为$qU$,由于洛伦兹力不做功,则加速$k$次后,带电粒子的动能增量为$kqU$,加速$k$次后,由动能定理有$kqU=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}$
解得$v=\sqrt{v_{0}^{2}+\dfrac{2kqU}{m}}=\dfrac{\sqrt{m^{2}v_{0}^{2}+2kqUm}}{m}$
故$\rm BC$错误;
$\rm D$.粒子在偏转磁场中运动的半径为$R$,则有$qvB=m\dfrac{v^{2}}{R}$
联立解得$B=\dfrac{mv}{qR}=\dfrac{m}{qR}\sqrt{v_{0}^{2}+\dfrac{2kqU}{m}}=\dfrac{\sqrt{m^{2}{v_{0}}^{2}+2kmqU}}{qR}$
故$\rm D$错误。
故选:$\rm A$。
高中 | 动能定理解决多过程问题题目答案及解析(完整版)
