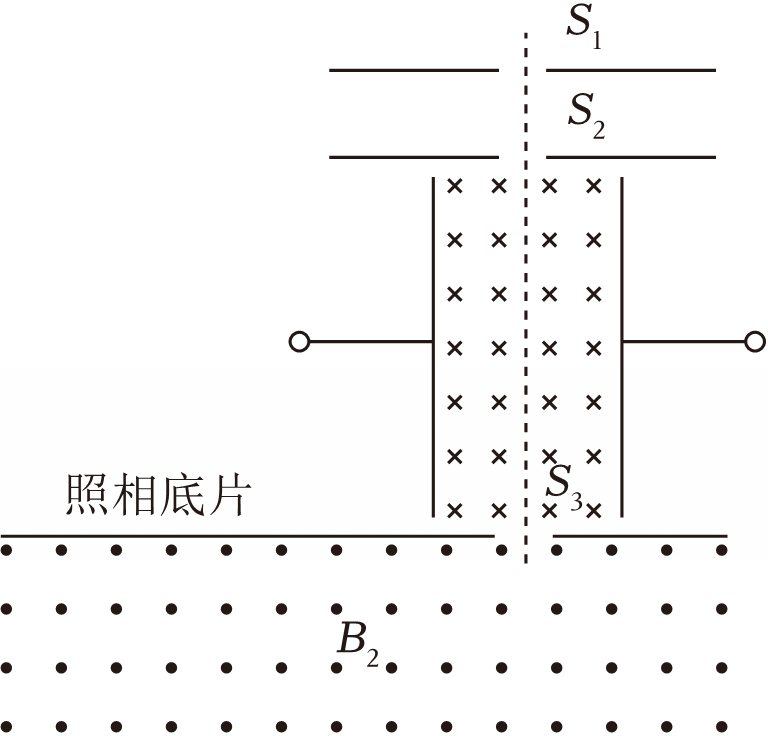
求$\rm _{2}^{3}He$在速度选择器中受的洛伦兹力$f$；

$\\rm _{2}^{3}He$在速度选择器中受的洛伦兹力$f$为$qE$

$\rm _{2}^{3}He$粒子在速度选择器中受洛伦兹力和电场力作用，做匀速直线运动。

所以洛伦兹力：$f=F_{电}=qE$

求加速电场对$\rm _{2}^{3}He$粒子所做的功$W$；

加速电场对$\\rm _{2}^{3}He$粒子所做的功$W=\\dfrac{B_{2}^{2}q^{2}d^{2}}{8m}$

偏转磁场中，$\rm _{2}^{3}He$粒子做匀速圆周运动的半径：$r_{1}=\dfrac{d}{2}$

根据洛伦兹力提供向心力有：$qvB_{2}= \dfrac{mv^{2}}{r_{1}}$

解得：$v= \dfrac{B_{2}qd}{2m}$

在加速电场中，根据动能定理：$W= \dfrac{1}{2}mv^{2}$

代入数据可得：$W=\dfrac{B_{2}^{2}q^{2}d^{2}}{8m}$

若有$\rm _{2}^{3}He$、$\rm _{2}^{4}He$、$\rm _{2}^{5}He$粒子以速度为$v=v_{0}±\Delta v$从$S_{2}$点射入，在速度选择器中运动可看成是速度为$v_{0}$的匀速直线运动和速度为$\Delta v$的匀速圆周运动的合运动，且均能从$S_{3}$点进入偏转磁场，在照相底片上出现$3$个有一定宽度的感光区域。为能区分$3$个感光区域，则该速度选择器极板间的最大间距$x$。

为能区分$3$个感光区域，则该速度选择器极板间的最大间距$x$为$\\dfrac{B_{2}}{3B_{1}}d$

因三种粒子电荷量相同，在速度选择器中可看成速度为$v_{0}$的匀速直线运动和速度为$\Delta v$的匀速圆周运动的合运动，则 $v_{0}=v= \dfrac{B_{2}qd}{2m}$

粒子在速度选择器中做圆周运动分运动的最大半径为$\dfrac{x}{4}$。

根据粒子在磁场中做圆周运动的半径公式，对三种粒子都有：$\dfrac{x}{4}=\dfrac{m \times \Delta v_{1}}{qB_{1}}=\dfrac{4m \times \Delta v_{2}}{3qB_{1}}=\dfrac{5m \times \Delta v_{3}}{3qB_{1}}$

$\rm _{2}^{3}He$在偏转磁场中的最大直径为：$D_{m1}= \dfrac{2m(v_{0}+\Delta v_{1})}{qB_{2}}$

结合以上结论有：$D_{m1}=d+ \dfrac{2m \times \Delta v_{1}}{qB_{2}} =d+ \dfrac{2m\Delta v_{1}}{qB_{1}} \times \dfrac{B_{1}}{B_{2}} =d+ \dfrac{x}{2} \times \dfrac{B_{1}}{B_{2}}$

同理$\rm _{2}^{4}He$的最小直径为：$D_{m2}= \dfrac{2 \times \dfrac{4}{3}m(v_{0}+\Delta v_{2})}{qB_{2}}=\dfrac{4}{3}d-\dfrac{x}{2} \times \dfrac{B_{1}}{B_{2}}\gt D_{m1}$

解得：$x\lt \dfrac{B_{2}}{3B_{1}}d$

同理$ _{2}^{4}He$的最大直径为：$D_{m2}'=\dfrac{4}{3}d+\dfrac{x}{2} \times \dfrac{B_{1}}{B_{2}}$

$ _{2}^{5}He$的最小直径为：$D_{m3}= \dfrac{2 \times \dfrac{5}{3}m(v_{0}+\Delta v_{3})}{qB_{2}}-\dfrac{x}{2} \times \dfrac{B_{1}}{B_{2}}\gt D_{m2}^\prime$

解得：$x\lt \dfrac{B_{2}}{3B_{1}}d$

因粒子在速度选择器中$B_{1}qv_{0}=qE$

联立解得：$B_{1}=\dfrac{2mE}{B_{2}qd}$

因此该速度选择器的极板间最大间距为$\dfrac{B_{2}}{3B_{1}}d$