如图甲是儿童正在进行喜爱的套圈游戏，游戏规则是将套圈从边界的上方抛出，套中物体获得胜利。其简易图如图乙所示，假设游戏者将套圈由虚线上不同的位置沿水平方向抛出，均能套中放在$B$点的玩偶，忽略空气阻力。则下列说法正确的是$(\qquad)$

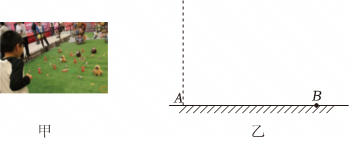
套圈抛出瞬间的速度与抛出点的高度无关

抛出点的位置越高，套圈落地瞬间，速度方向与水平方向的夹角越小

抛出点的位置越高，套圈落地瞬间的速度越大

抛出点的位置越高，落地瞬间重力的瞬时功率越大

$\rm A$、平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。设套圈抛出点的高度为$h$，水平位移为$x$，抛出瞬间的水平速度为$v_{0}$，运动时间为$t$。则在竖直方向：根据自由落体运动的位移公式$h=\dfrac{1}{2}gt^{2}$，可得运动时间为：$t=\sqrt{\dfrac{2h}{g}}$

水平方向：根据匀速直线运动的位移公式可得：$x=v_{0}t$，解得：$v_{0}=x\sqrt{\dfrac{g}{2h}}$，由此可知套圈抛出瞬间的水平速度$v_{0}$与抛出点的高度$h$有关，抛出点高度越高，抛出瞬间的速度越小，故$\rm A$错误；

$\rm B$、设套圈落地瞬间速度方向与水平方向的夹角为$\theta$，根据平抛运动的规律可知$\tan\theta=\dfrac{v_{y}}{v_{0}}$，其中：$v_{y}=\sqrt{2gh}$，$v_{0}=x\sqrt{\dfrac{g}{2h}}$，则$\tan\theta=\dfrac{v_{y}}{v_{0}}=\dfrac{\sqrt{2gh}}{x\sqrt{\dfrac{g}{2h}}}=\dfrac{2h}{x}$，因为$x$为定值，抛出点的位置越高，$h$越大，则$\tan\theta$越大，$\theta$越大，即套圈落地瞬间速度方向与水平方向的夹角越大，故$\rm B$正确；

$\rm C$、套圈落地瞬间的速度为：$v=\sqrt{v_{0}^{2}+v_{y}^{2}}=\sqrt{\left(x\sqrt{\dfrac{g}{2h}}\right)^{2}+(\sqrt{2gh})^{2}}=\sqrt{\dfrac{x^{2}g}{2h}+2gh}$，根据均值不等式的性质可知，当$\dfrac{x^{2}g}{2h}=2gh$时，$\dfrac{x^{2}g}{2h}+2gh$取得最小值。所以抛出点的位置越高，$h$越大，套圈落地瞬间的速度不一定越大，故$\rm C$错误；

$\rm D$、重力的瞬时功率为：$P=mgv_{y}$，其中：$v_{y}=\sqrt{2gh}$，则有：$P=mg\sqrt{2gh}$，因为$m$、$g$为定值，抛出点的位置越高，$h$越大，所以落地瞬间重力的瞬时功率越大，故$\rm D$正确。

故选：$\rm D$。