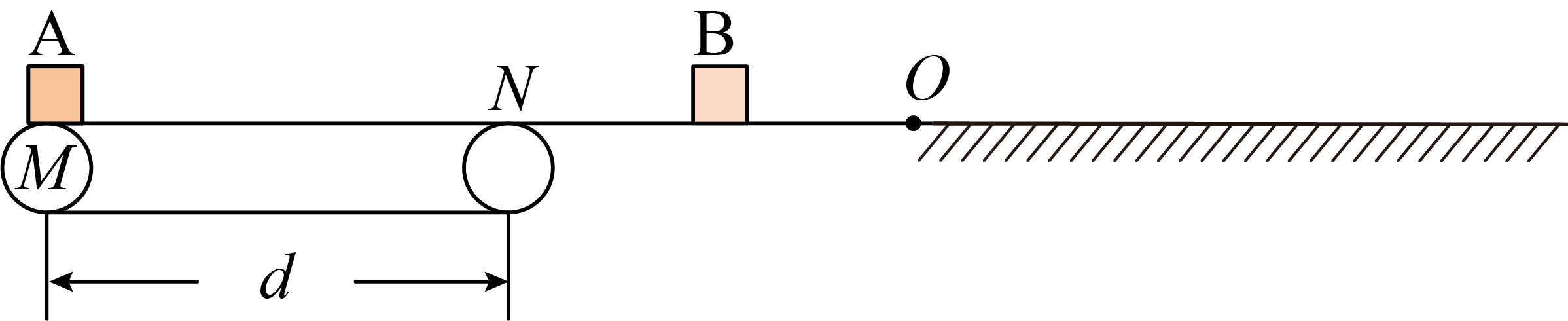
求$A$在传送带上的加速度大小及离开传送带时的速度大小；

$a=\\mu g$，$v_{1}=\\sqrt{2\\mu gd}$

$A$在传送带上由滑动摩擦力提供加速度，即$\mu mg=ma$

可得$a=\mu g$

由于$A$还没与传送带达到相同速度时就离开传送带，所以物体在传送带上做匀加速直线运动，由$v_{1}^{2}=2ad$

解得$v_{1}=\sqrt{2\mu gd}$

若碰前瞬间，$B$的速度大小为$A$的一半，碰撞为弹性碰撞，且碰后$A$、$B$在粗糙地面上停下后相距$d$，求$B$的质量；

$M=\\dfrac{m}{3}$

设$B$的质量为$M$，则由题意由碰前$v_{\rm A}=v_{1}$，$v_{\text{B}}= \dfrac{v_{1}}{2}$，两物体发生弹性碰撞则动量和能量守恒有$mv_{1}+M\dfrac{v_{1}}{2}=m{v'}_{1}+ M{v'}_{2}$，$\dfrac{1}{2}mv_{1}^{2}+ \dfrac{1}{2}M\left( \dfrac{v_{1}}{2} \right)^{2}= \dfrac{1}{2}m{v'}_{1}^{2}+\dfrac{1}{2}M{v'}_{2}^{2}$

又因为在弹性碰撞中，碰前相对速度与碰后相对速度大小相等，方向相反，即$v_{1}-\dfrac{v_{1}}{2}={v'}_{2}-{v'}_{1}=\dfrac{v_{1}}{2}$

联立解得${v'}_{1}=\dfrac{mv_{1}}{m+M}$，${v'}_{2}=\dfrac{(3m+M)v_{1}}{2(m+M)}$

因为$OP$ 段粗糙，由动能定理有$- \mu mgs=0-\dfrac{1}{2}mv^{2}$

得$s=\dfrac{v^{2}}{2\mu g}$，即$s_{\text{A}}=\dfrac{{v'}_{1}^{2}}{2\mu g}$，$s_{\text{B}}=\dfrac{{v'}_{2}^{2}}{2\mu g}$

根据题意有$s_{\rm B}-s_{\rm A}=d$，且由（$1$）有$v_{1}=\sqrt{2\mu gd}$

联立各式解得$M=\dfrac{m}{3}$

若$B$的质量是$A$的$n$倍，碰后瞬间$A$和$B$的动量相同，求$n$的取值范围及碰后瞬间$B$的速度大小范围。

$\\dfrac{1}{3}\\lt n \\leqslant 1$，$\\dfrac{\\sqrt{2\\mu gd}}{2}\\lt v_{\\text{B}}\\lt 2\\sqrt{2\\mu gd}$

设碰前小物块$B$向右运动的速度为$v_{\rm B0}$，$A$、$B$发生碰撞，则$v_{\rm B0}\lt v_{1}$

$A$、$B$碰撞过程动量守恒有$mv_{1}+nmv_{B0}=mv_{\rm A}+nmv_{\rm B}$

又因为碰后瞬间$A$和$B$的动量相同，则$mv_{\rm A}=nmv_{\rm B}\gt 0$

则$v_{\text{B}}=\dfrac{v_{1}+nv_{\rm B0}}{2n}$，$v_{\text{A}}=\dfrac{v_{1}+nv_{\rm B0}}{2}$

根据碰撞的约束条件，要两物块不发生二次碰撞则有$v_{\rm A}\leqslant v_{\rm B}$，即$n\leqslant 1$

碰后动能不增，即$\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}mv_{\rm B0}^{2} \geqslant \dfrac{1}{2}m\left( \dfrac{v_{1}+nv_{\rm B0}}{2} \right)^{2}+\dfrac{1}{2}(nm)\left( \dfrac{v_{1}+nv_{\rm B0}}{2n} \right)^{2}$，可得$n\gt \dfrac{1}{3}$

所以$n$的取值范围为$\dfrac{1}{3}\lt n\leqslant 1$

分别将$n=1$和$n=\dfrac{1}{3}$代入$v_{\text{B}}=\dfrac{v_{1}+nv_{B0}}{2n}$，分别可得$v_{\text{B}}=\dfrac{v_{1}+v_{\rm B0}}{2}\gt \dfrac{v_{1}}{2}$，$v_{\text{B}}'=\dfrac{3v_{1}+v_{\rm B0}}{2}\lt 2v_{1}$

所以对应的$B$ 的速度范围为$\dfrac{v_{1}}{2}\lt v_{\text{B}}\lt 2v_{1}$，代入$v_{1}=\sqrt{2\mu gd}$

可得$\dfrac{\sqrt{2\mu gd}}{2}\lt v_{\text{B}}\lt 2\sqrt{2\mu gd}$