| 探究两个互成角度的力的合成规律 题目答案及解析
稿件来源:高途
| 探究两个互成角度的力的合成规律题目答案及解析如下,仅供参考!
必修1
第三章 相互作用
3.4 力的合成
探究两个互成角度的力的合成规律
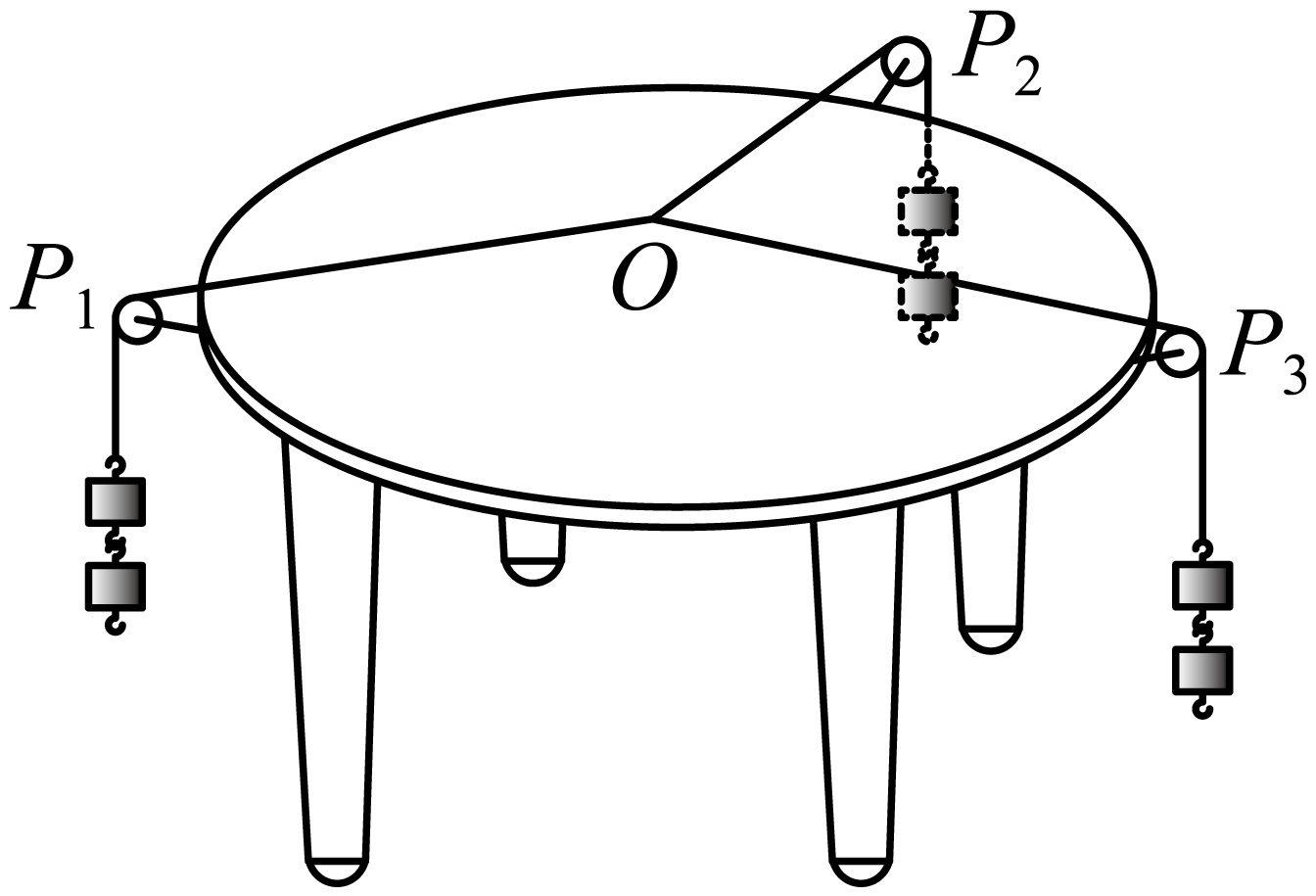
某物理实验小组用如图所示器材探究两个互成角度的力的合成规律。在圆形水平桌面上平铺并固定一张白纸,在桌子边缘安装三个光滑的滑轮,其中滑轮$P_{2}$固定在桌子边,滑轮$P_{1}$、$P_{3}$可沿桌边移动。三根绳子系在同一点$O$,在每根轻绳下分别挂上一定数量的钩码,并使结点$O$(不与桌面接触)静止。(已知$\sin37^\circ =0.6$,$\cos37^\circ =0.8$)
若一根绳挂的钩码质量为$4m$,另一根绳挂的钩码质量为$12m$,则第三根绳挂的钩码质量一定不小于 ;
两个力合成时,合力范围为$|F_{1}-F_{2}|\leqslant F\leqslant F_{1}+F_{2}$
已知两个力对应的钩码质量为$4m$和$12m$,则两力大小分别为$F_{1}=4mg$,$F_{2}=12mg$,合力范围是$8mg\leqslant F\leqslant 16mg$
第三根绳的拉力应与这两个力的合力等大反向,所以第三根绳挂的钩码质量对应的重力至少为$8mg$,即质量一定不小于$8m$
若滑轮$P_{1}$下所挂的钩码质量为$10m$、滑轮$P_{2}$、$P_{3}$下所挂的钩码质量分别为$8m$、$6m$,则当结点$O$静止时,轻绳$OP_{1}、OP_{2}$之间的夹角$∠P_{1}OP_{2}$大小为 。
三个力大小分别为$F_{1}=10mg$,$F_{2}=8mg$,$F_{3}=6mg$
因为$(6mg)^{2}+(8mg)^{2}=(10mg)^{2}$
根据勾股定理逆定理可知,$8mg$和$6mg$这两个力垂直,画出力的平行四边形,$6mg$的力对应的角为$37^\circ $,所以轻绳$OP_{1}$、$OP_{2}$之间的夹角$∠P_{1}OP_{2}$大小为$143^\circ $
若保持($2$)中滑轮$P_{1}$下所挂的钩码不变,滑轮$P_{1}$和$P_{2}$位置不变,将滑轮$P_{2}$下所挂的钩码质量变为$10m$,为了使整个系统保持平衡且$O$点位置不变,从俯视角度来看,需要把滑轮$P_{3}$ (选填“顺时针”或“逆时针”)移动一小段合适的距离且换上合适质量的钩码。
原来$P_{2}$、$P_{3}$对应的力分别为$8mg$、$6mg$,现在$P_{2}$对应的力变为$10mg$,要使$O$点位置不变,$P_{1}$对应的力$10mg$不变
根据平行四边形定则,$P_{1}$、$P_{2}$对应的力的合力大小$10mg$,方向位于$∠P_{1}OP_{2}$的角平分线上
要保持力的平衡,$P_{3}$对应的力的方向应调整,从俯视角度看,需要把滑轮$P_{3}$顺时针移动一小段合适的距离且换上合适质量的钩码。
| 探究两个互成角度的力的合成规律题目答案及解析(完整版)
