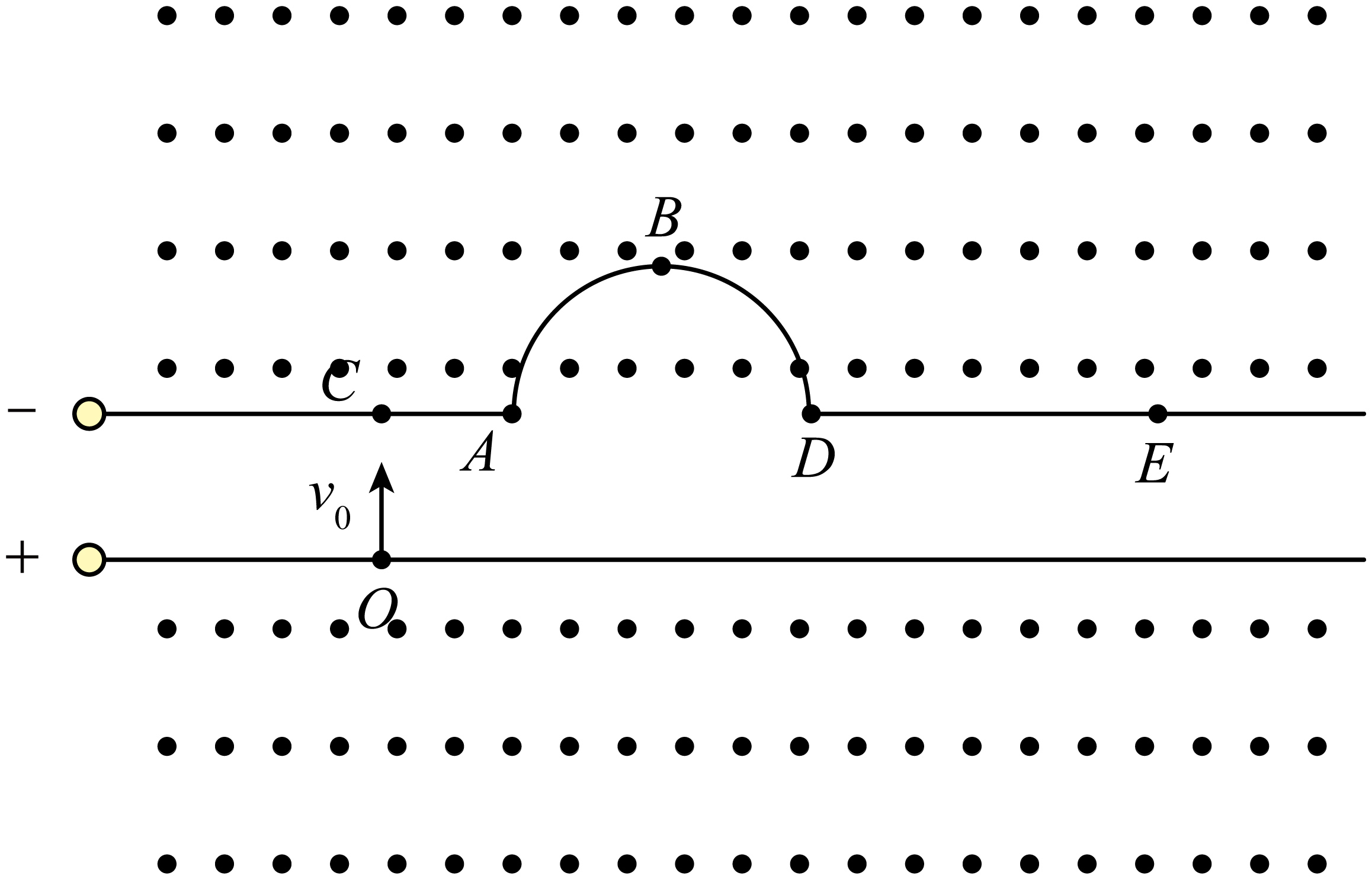
求粒子发射速度$v_{0}$的大小；

$v_{0}= \\dfrac{qBR}{2m}$

粒子在磁场中做匀速圆周运动，由几何知识可得，粒子圆周运动的轨道半径$r=\dfrac{R}{2}$

洛伦兹力提供圆周运动的向心力，则有$Bqv_{0}=\dfrac{mv_{0}^{2}}{r}$

联立解得$v_{0}=\dfrac{qBR}{2m}$

调整电压的大小，使粒子从上面打在挡板上$B$点，求粒子从$O$点出发打到$B$点时所需要的时间；

$t=\\dfrac{127\\pi m}{180qB}+ \\dfrac{8md}{7qBR}$

作出粒子在磁场中的运动轨迹，如图所示

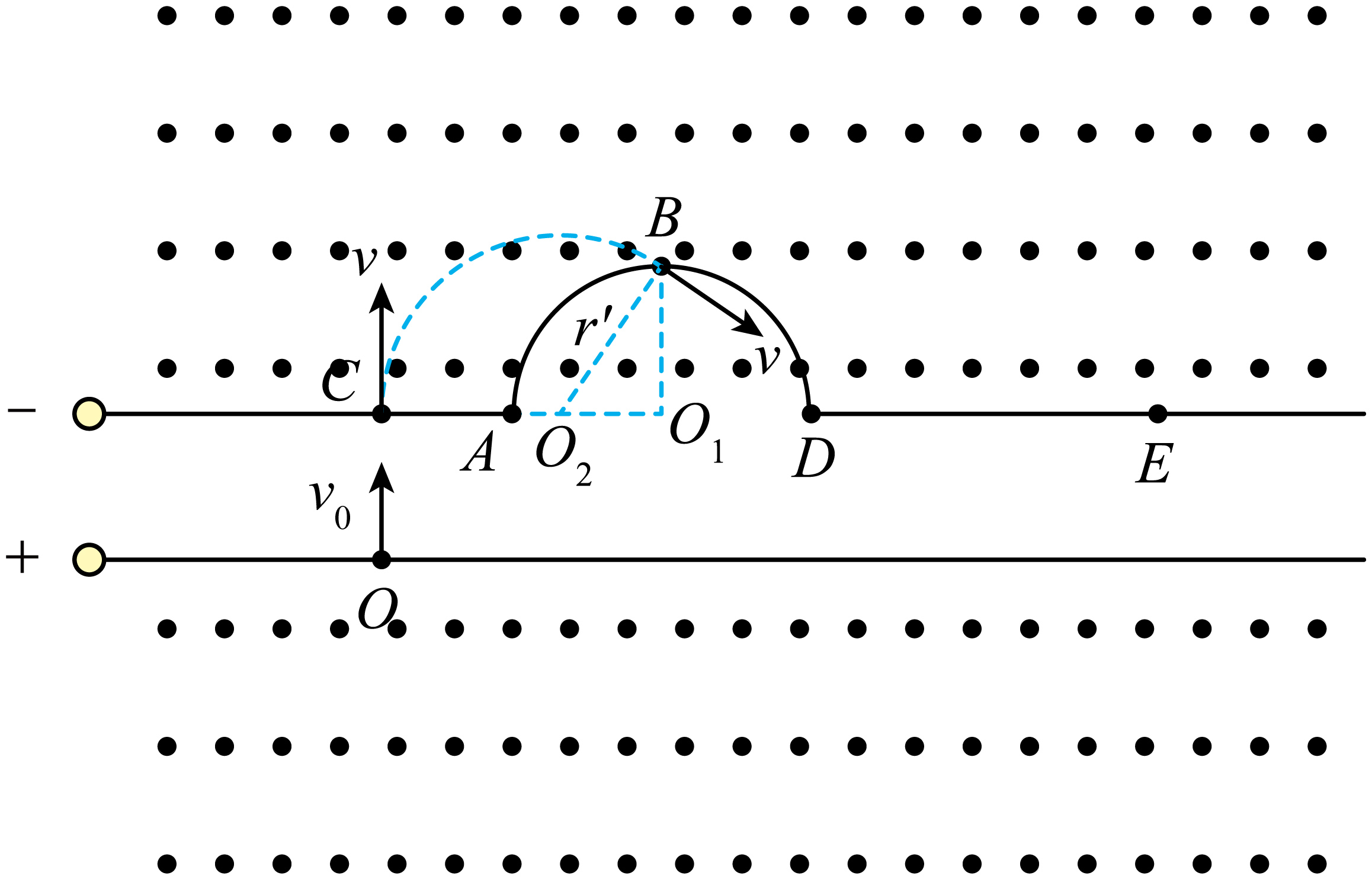
由几何知识可得$r'^{2}=(2R-r')^{2}+R^{2}$

解得$r'=\dfrac{5R}{4}$

又因为$Bqv=\dfrac{mv^{2}}{r'}$

解得$v'=\dfrac{5qBR}{4m}$

又因为$O_{1}O_{2}=2R-r'=\dfrac{3}{4}R$

故$\tan\angle BO_{2}O_{1}=\dfrac{R}{\dfrac{3}{4}R}=\dfrac{4}{3}$

解得$∠BO_{2}O_{1}=53^\circ $

粒子偏转的圆心角$\theta=180^\circ -53^\circ =127^\circ $

粒子在磁场中的运动周期$T=\dfrac{2\pi m}{Bq}$

粒子在磁场中的时间$t_{1}=\dfrac{127}{360}T=\dfrac{127\pi m}{180qB}$

粒子通过电场的时间$t_{2}=\dfrac{d}{v_{平均}}=\dfrac{8md}{7qBR}$

粒子打到$B$的时间$t=t_{1}+t_{2}=\dfrac{127\pi m}{180qB}+\dfrac{8md}{7qBR}$

若$DE=17R$，调整电压大小使粒子被粒子靶接收，求粒子靶能接收到粒子时的最小电压值。

$U_{\\min}= \\dfrac{589qB^{2}R^{2}}{288m}$

粒子在上下运动$2$个半圆一次会向右平移$\Delta l$，则有$\Delta l=2r-2r_{0}$

当粒子打中$E$点时，由几何关系可知$2r+n\Delta l=\overline{CE}$

即有$2r+n(2r-2r_{0})=20R(n=0, 1, 2, 3…)$

且$r\geqslant r_{2}=2R$

解得$n \leqslant \dfrac{16}{3}$

$n$可以取$0$，$1$，$2$，$3$，$4$，$5$共$6$种情况，当$n=5$时，可得最小轨道半径$r=\dfrac{25R}{12}$

速度大小$v=\dfrac{qBr}{m}=\dfrac{25qBR}{12m}$

根据动能定理$qU=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}$，$U_{\min}=\dfrac{589qB^{2}R^{2}}{288m}$