高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
如图所示,电子显像管由电子枪、加速电场、偏转磁场及荧光屏组成。在加速电场右侧有相距为$d$、长为$l$的两极板,两极板构成的矩形区域内存在方向垂直纸面向外的匀强磁场,磁场的右边界与荧光屏之间的距离也为$d$。荧光屏中点$O$与加速电极上两小孔$S_{1}$、$S_{2}$位于两板的中心线上。从电子枪发射质量为$m$、电荷量大小为$e$的电子,经电压为$U_{0}$的加速电场后从小孔$S_{2}$射出,经磁场偏转后,恰好从上极板右侧边缘离开磁场,最后打到荧光屏上。若$l=\dfrac{3d}{2}$,不计电子进入加速电场前的速度及其重力。
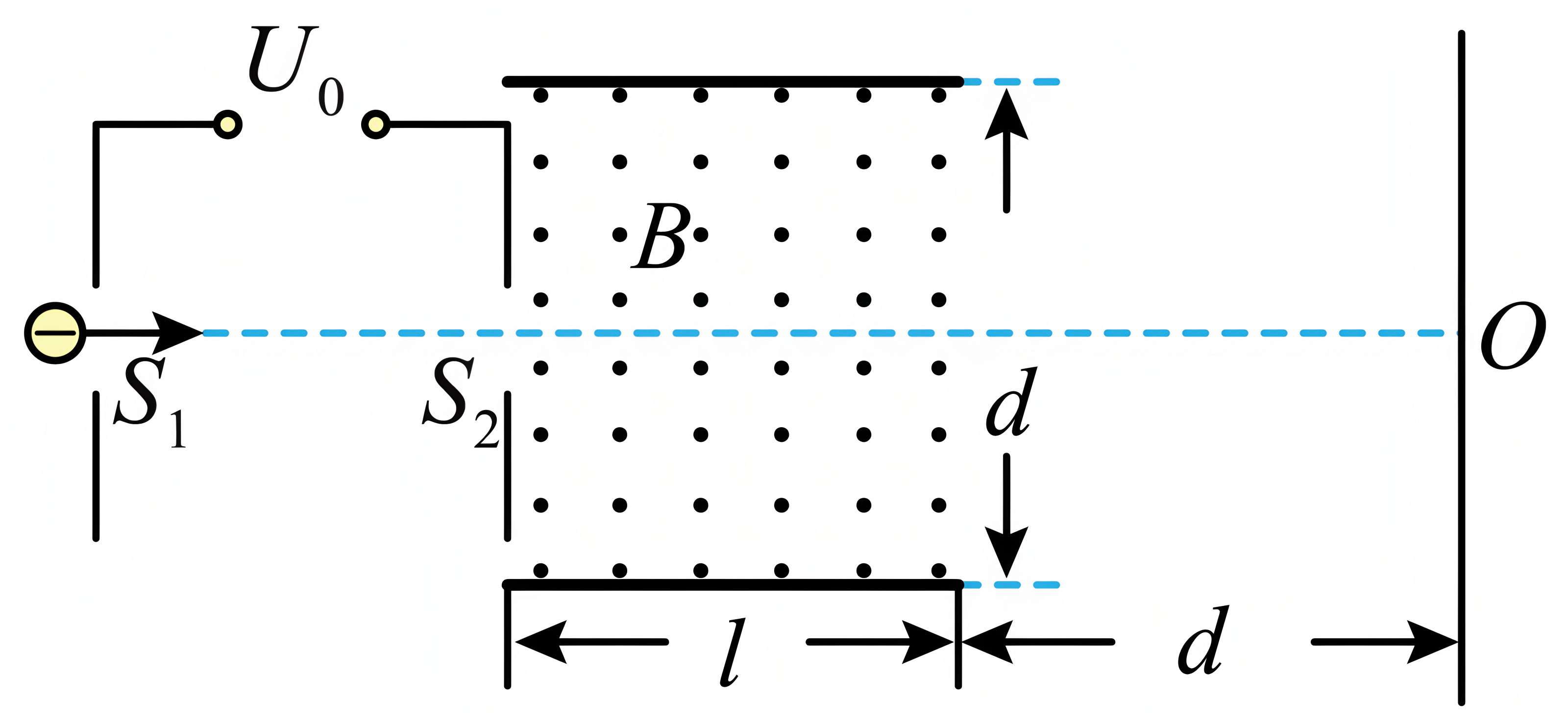
求电子进入磁场时的速度大小;
$v_{0}= \\sqrt{\\dfrac{2eU_{0}}{m}}$
"]]设电子经电场加速后的速度大小为$v_{0}$,由动能定理可得$eU_{0}=\dfrac{1}{2}mv_{0}^{2}-0$
解得$v_{0}=\sqrt{\dfrac{2eU_{0}}{m}}$
求磁场的磁感应强度$B$的大小;
$B= \\dfrac{2}{5d}\\sqrt{\\dfrac{2mU_{0}}{e}}$
"]]电子在磁场中偏转,经磁场偏转后,恰好从上极板右侧边缘离开磁场,即偏转后沿直线运动到荧光屏,如图所示
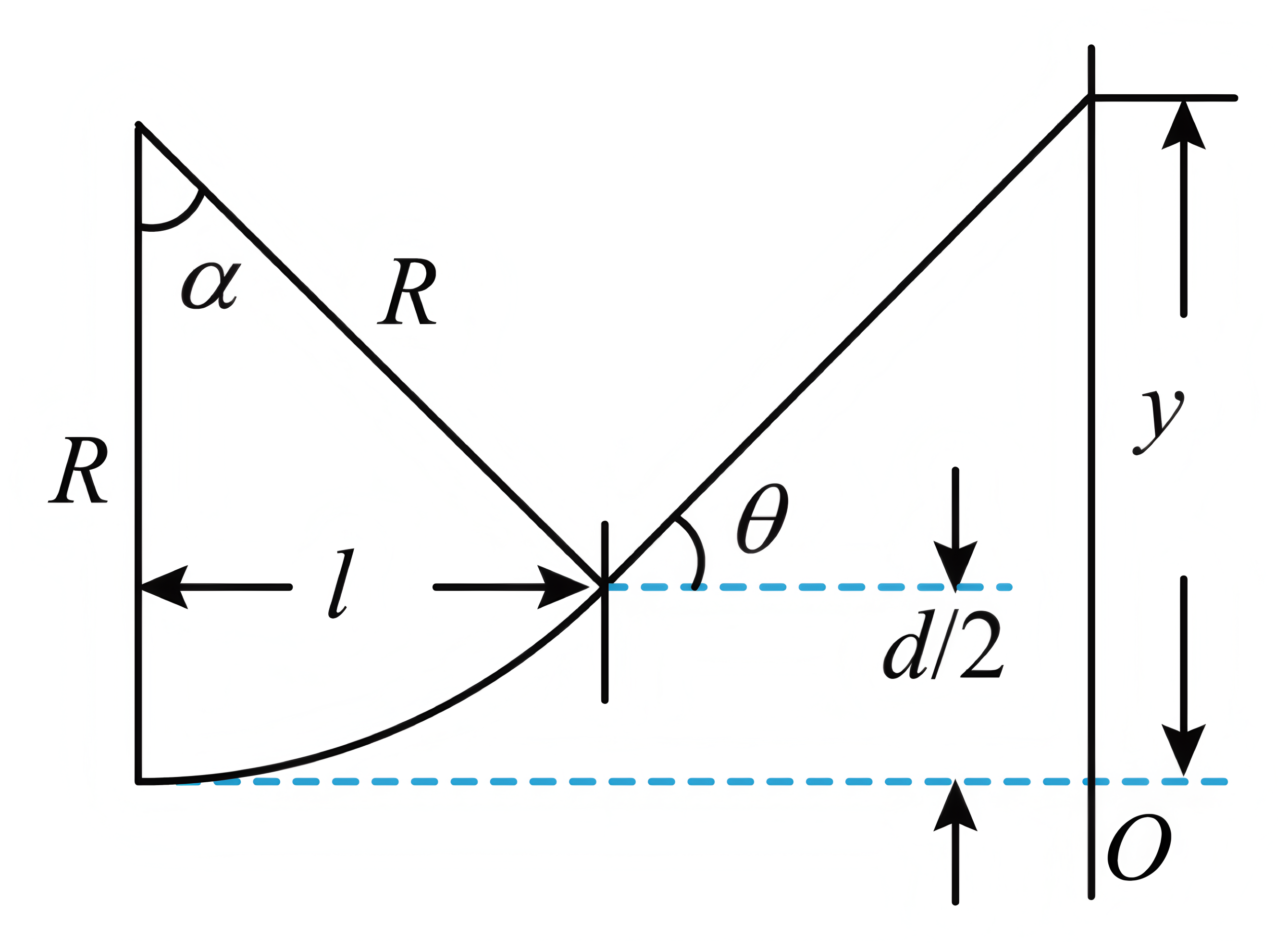
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可得$ev_{0}B=m\dfrac{v_{0}^{2}}{R}$
由几何知识可得$\left( R-\dfrac{d}{2} \right)^{2}+l^{2}=R^{2}$
已知$l=\dfrac{3}{2}d$,$v_{0}=\sqrt{\dfrac{2eU_{0}}{m}}$
解得$R=\dfrac{5}{2}d$,$B=\dfrac{2}{5d}\sqrt{\dfrac{2mU_{0}}{e}}$
求电子到达荧光屏的位置与$O$点距离$y$。
$y=\\dfrac{5}{4}d$
"]]由解析图可知,粒子到达荧光屏的位置与$O$点的距离为$y$,由几何知识可得$\tan\alpha=\dfrac{l}{R-\dfrac{d}{2}}=\tan\theta =\dfrac{y-\dfrac{d}{2}}{d}$
解得$y=\dfrac{5}{4}d$
若要电子沿直线到达$O$点,两极板间再加上竖直方向的匀强电场,求所加电场强度大小及方向。
$E= \\dfrac{4U_{0}}{5d}$,方向竖直向上
"]]根据平衡条件可知$qBv=qE$
解得$E=Bv=\dfrac{2}{5d}\sqrt{\dfrac{2mU_{0}}{e}}\sqrt{\dfrac{2eU_{0}}{m}}=\dfrac{4U_{0}}{5d}$
方向竖直向上。
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
