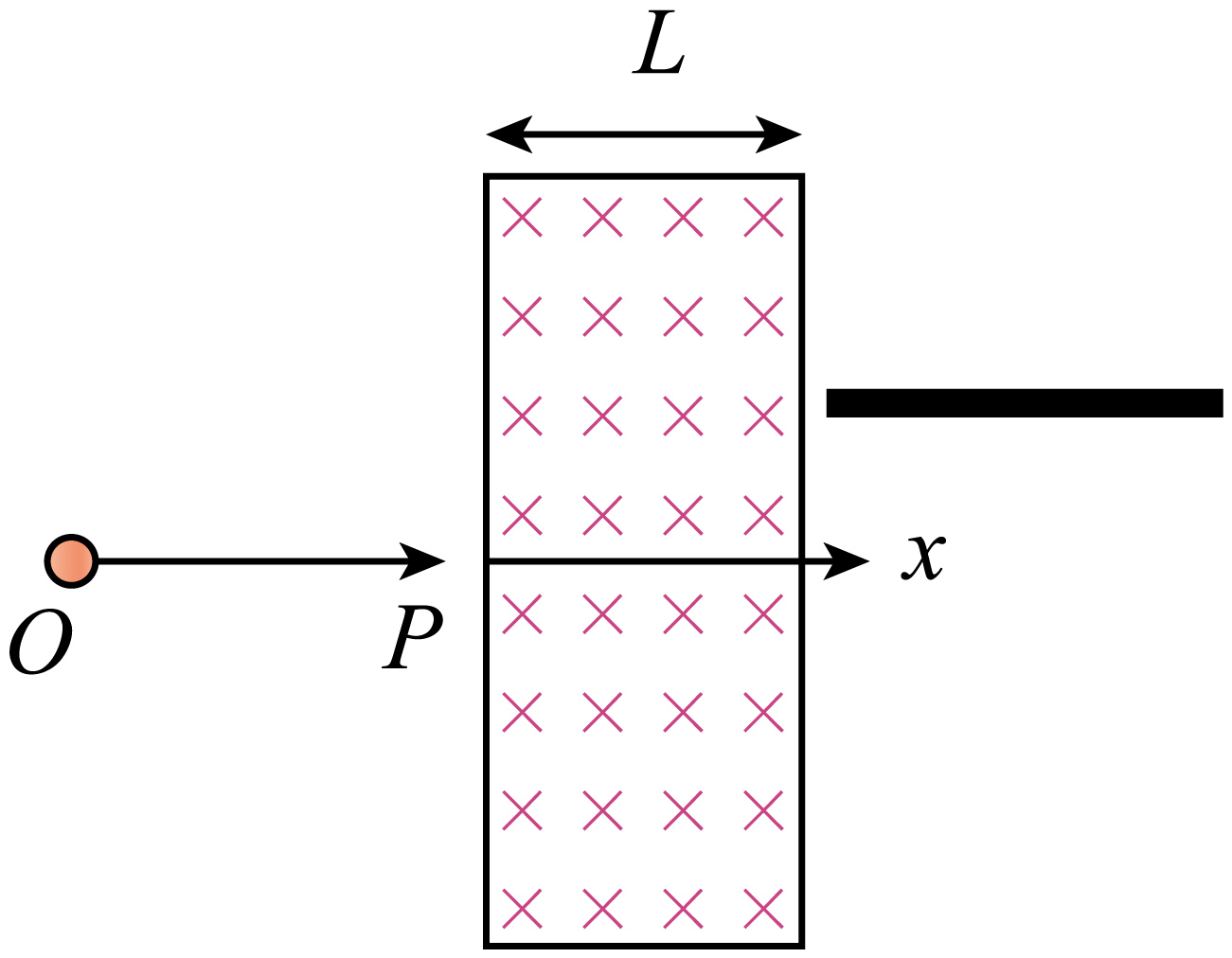
单个光子的等效质量$m$；

$5\\times10^{-36}\\;\\rm kg$

光子的能量为$E=hv= \dfrac{hc}{\lambda}$

根据质能方程可知，光子的等效质量为$m^{}=\dfrac{E}{c^{2}}=\dfrac{h}{\lambda c}$

解得$m=\dfrac{E}{c^{2}}=\dfrac{h}{\lambda c}=\dfrac{6.63 \times 10^{- 34}}{442 \times 10^{- 9} \times 3 \times 10^{8}}\;\text{kg}=5 \times 10^{- 36}\; \text{kg}$

光子在晶体中的轨迹半径$r$和偏转位移$d$；

$r=1\\;\\rm m$，$d=0.2\\;\\rm m$

洛伦兹力充当向心力，故有$qvB_{0}= \dfrac{mv^{2}}{r}$

解得$r=\dfrac{mv}{qB_{0}}=\dfrac{5 \times 10^{- 36} \times 2 \times 10^{8}}{1.6 \times 10^{- 19} \times 0.625 \times 10^{- 8}}\;\text{m}=1\;\rm \text{m}$

根据几何关系有$\sin\theta=\dfrac{L}{r}=0.6$，$d=r(1-\cos\theta)=0.2r=0.2\;\rm m$

若磁场存在梯度分布：以$P$点为坐标原点，$B=B_{0}(1-\beta x)$，$\beta=1\;\rm m^{-1}$，求激光束打在探测板上对探测板的作用力$F$（仅考虑出射晶体时的折射情况）；

$4.2\\times10^{-11}\\;\\rm N$

将粒子的速度分解，在$y$方向上的洛伦兹力与水平分速度有关，列动量定理，有$∑Bqv_{x}⋅\Delta t=mv_{y}-0$

即$∑B_{0}(1-\beta x)q⋅\Delta x=mv_{y}-0$

可解得$B_{0}qx-B_{0}q\dfrac{x^{2}}{2}=mv_{y}$

所以$v_{y}=0.84\times10^{8}\;\rm m/s$

方向为$\sin\theta=\dfrac{v_{y}}{v}=0.42$

根据折射率公式，有$n=\dfrac{\sin\alpha}{\sin\theta}$

碰撞时有动量定理，可知$F=\dfrac{2P\sin\alpha}{c}=\dfrac{2 \times 10^{- 2} \times 0.63}{3 \times 10^{8}}\;\rm \text{N}=4.2 \times 10^{- 11}\;\rm \text{N}$

若可调节晶体折射率，使光子在晶体中速度可在$0 ∼ 2 \times 10^{8}\;\rm m/s$范围内变化，光从$P$点进入一块上述光子晶体，$OP=1m$，请你设计光子晶体的形状，使光子在以上速度范围内经过晶体内磁场偏转后都可以回到$O$点，画出晶体形状，并计算最小面积。（不考虑进出晶体界面处由于折射反射引起的方向改变）

图示见解析；$\\left( \\dfrac{\\pi}{2}+1 \\right)\\;\\text{m}^{2}$

由于$r=\dfrac{mv}{qB_{0}}$

当$v=2 \times 10^{8}\;\rm m/s$时，$r_{\max}=1\;\rm m$

如图所示，曲线$1$为速度最大值时对应的轨迹，曲线$2$为速度为$v$时对应的一般轨迹，假设出射点为$A(x,y)$。

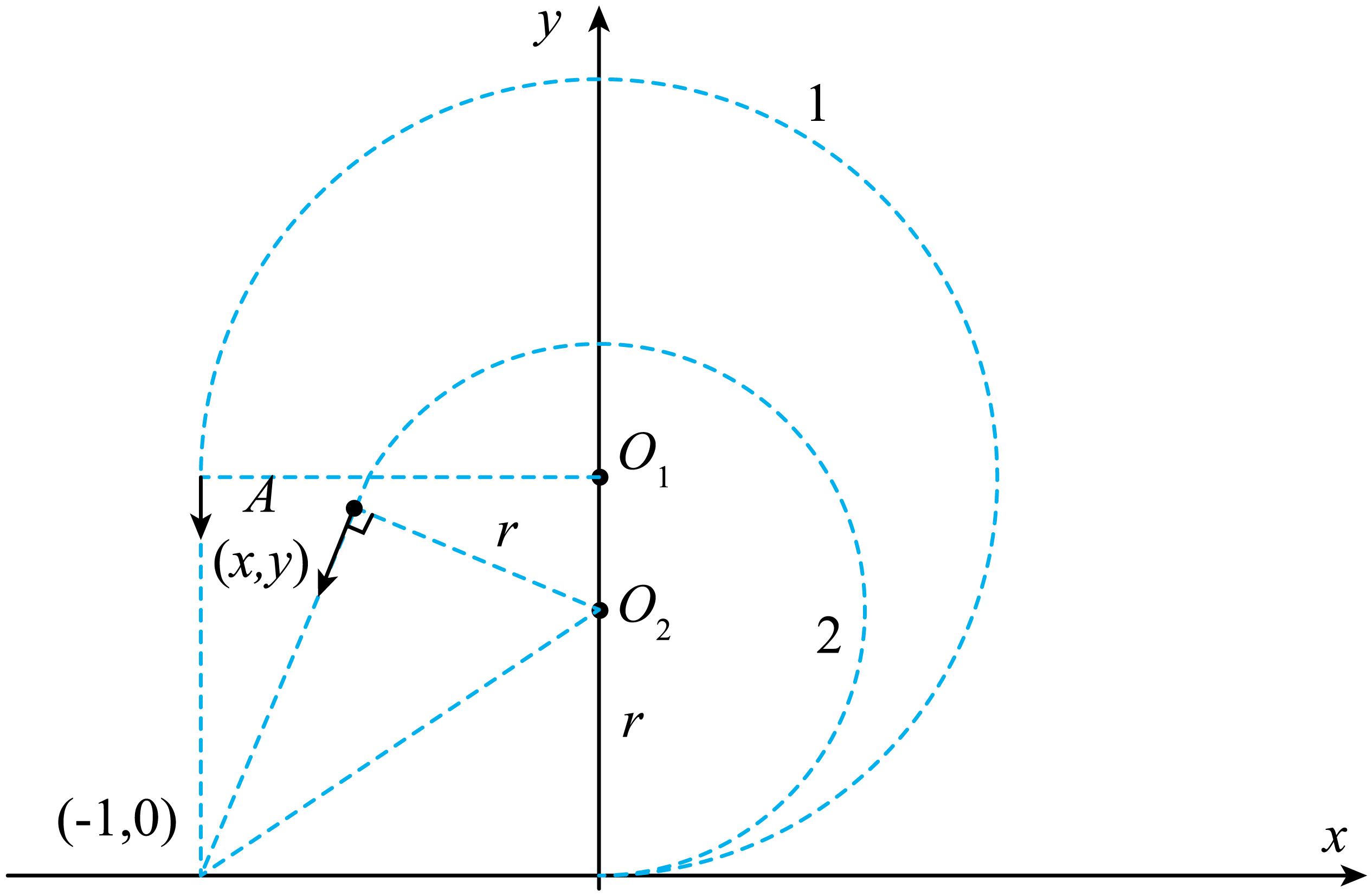
由几何关系得$r^{2}+(x+1)^{2}+y^{2}=1+r^{2}$，$(x+1)^{2}+y^{2}=1$

即所有出射点连接起来为圆弧。所以满足题意可设计如下图所示形状的光子晶体。

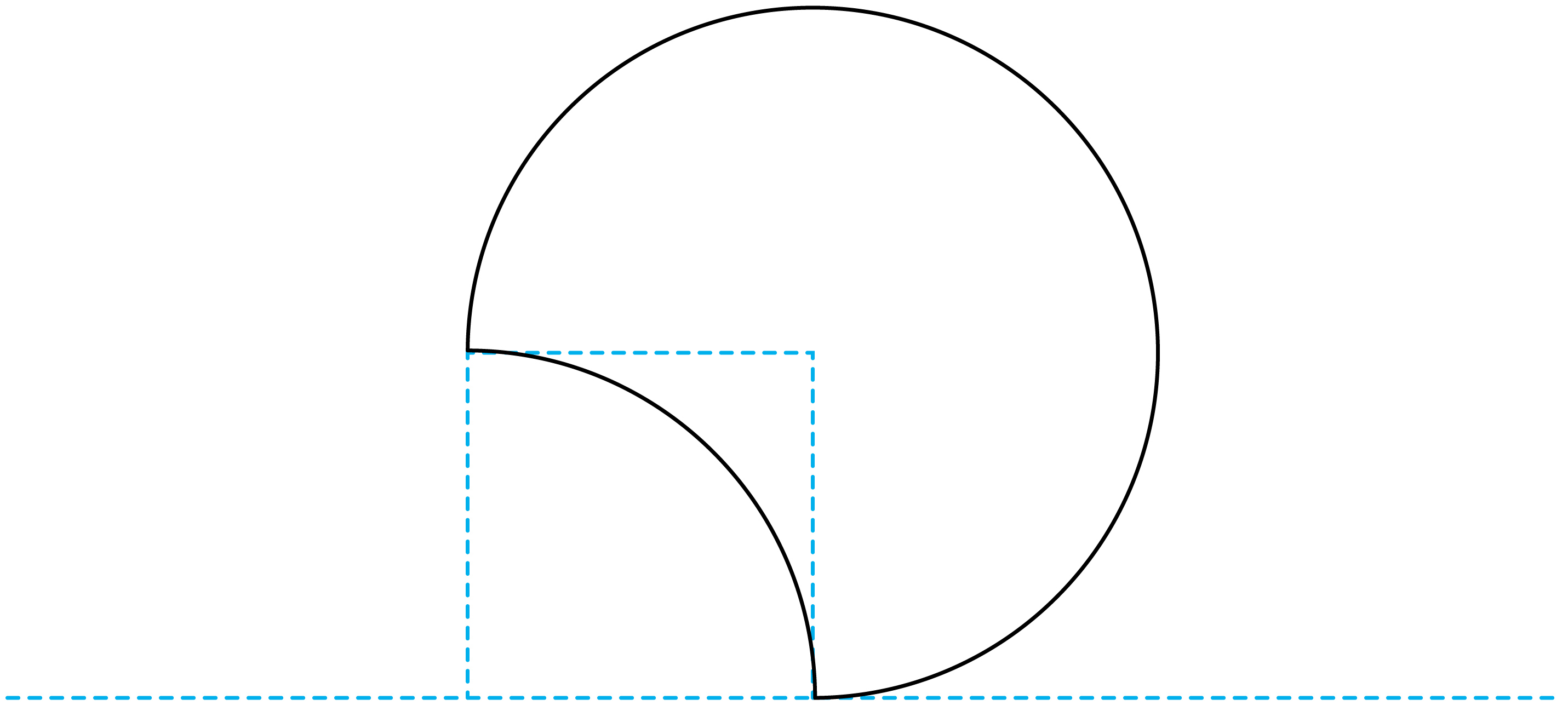
则光子晶体的最小面积为$s_{\min}=\dfrac{3}{4}\pi r_{\max}^{2}+\left( r_{\max}^{2}-\dfrac{1}{4}\pi r_{\max}^{2} \right)=\left( \dfrac{\pi}{2}+1 \right)\;\text{m}^{2}$