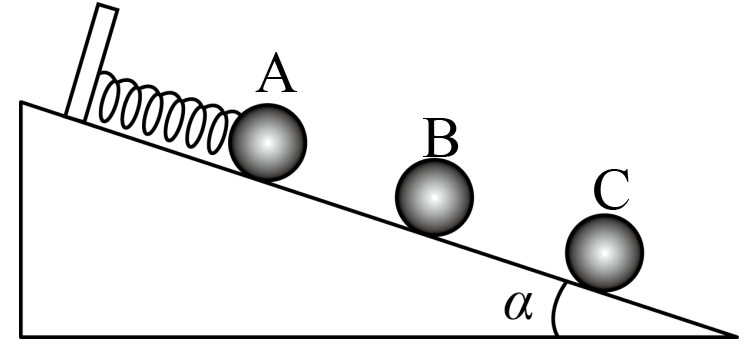
如图所示，在倾角为$\alpha$的光滑绝缘斜面上固定一个挡板，在挡板上连接一根劲度系数为$k_{0}$的绝缘轻质弹簧，弹簧另一端与$A$球连接。$A$、$B$、$C$三小球的质量均为$M$，$q_{\rm A}=q_{0}\gt 0$，$q_{B}=-q_{0}$，当系统处于静止状态时，三小球等间距排列。已知静电力常量为$k$，则$(\qquad)$

$q_{\\text{C}}=\\dfrac{4}{7}q_{0}$

弹簧伸长量为$\\dfrac{Mg\\sin\\alpha}{k_{0}}$

$A$球受到的库仑力大小为$2Mg$

相邻两小球间距为$q_{0}\\sqrt{\\dfrac{3k}{8Mg}}$

$\rm A$．对$C$球进行受力分析可得，它受到$2$个方向相反的库仑力、重力、支持力，由于$A$与$B$、$B$与$C$间距相等，由库仑定律可得，$B$对$C$的库仑力是$A$对$C$库仑力的$4$倍，因此$C$球应为正电荷才能受力平衡。设$A$、$B$间距为$l$，对$B$进行受力分析，由平衡条件可得$Mg\sin\alpha+k\dfrac{q_{0}q_{\text{C}}}{l^{2}}=k\dfrac{q_{0}q_{\text{0}}}{l^{2}}$

对$C$进行受力分析，由平衡条件可得$Mg\sin\alpha+k\dfrac{q_{0}q_{\text{C}}}{(2l)^{2}}=k\dfrac{q_{0}q_{\text{C}}}{l^{2}}$

联立解得$q_{\text{C}}=\dfrac{4}{7}q_{0}$

故$\rm A$正确；

$\rm B$．把$A$、$B$、$C$三小球看作整体，设弹簧伸长量为$x$，由平衡条件可知$k_{0}x=3Mg\sin\alpha$

解得$x=3\dfrac{Mg\sin\alpha}{k_{0}}$

故$\rm B$错误；

$\rm C$．对$A$进行受力分析，设$A$球受到的库仑力大小为$F$，由平衡条件可知$k_{0}x=Mg\sin\alpha+F$

解得$F=2Mg\sin a$

故$\rm C$错误；

$\rm D$．由$Mg\sin\alpha+k\dfrac{q_{0}q_{\text{C}}}{l^{2}}=k\dfrac{q_{0}q_{0}}{l^{2}}$

可得$l=q_{0}\sqrt{\dfrac{3k}{7Mg\sin\alpha}}$

故$\rm D$错误。

故选：$\rm A$。