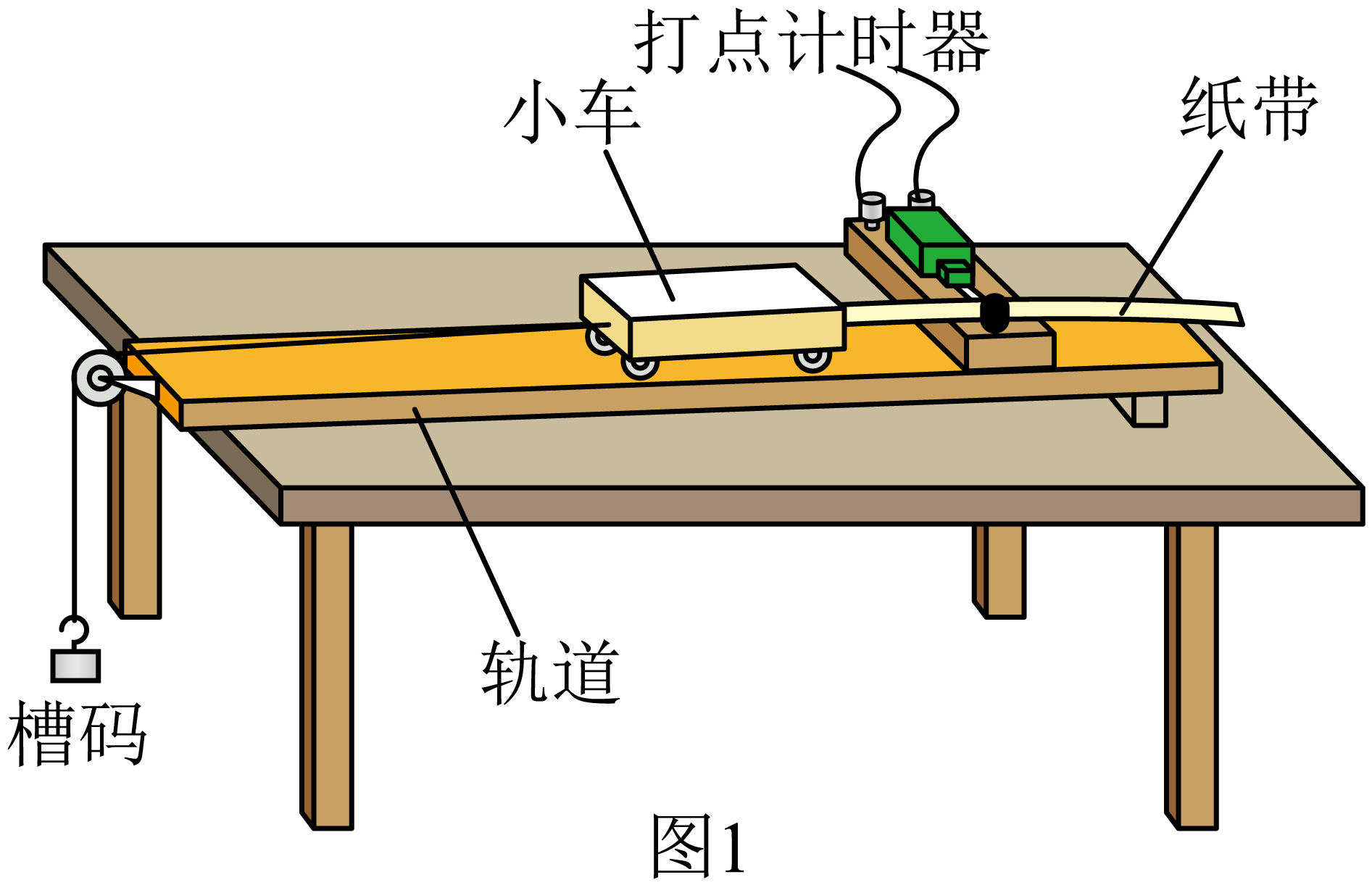
关于该实验操作，下列说法正确的是$(\quad\ \ \ \ )$

挂小质量的槽码用以补偿小车运动过程中受到的阻力

小车内要装钩码以增大小车质量，需重新补偿阻力

调节定滑轮的高度，使牵引小车的细线与木板平行

操作中，若先释放小车再接通电源，得到的纸带一定不可用

$\rm A$．挂小质量的槽码使小车做加速运动，在木板下垫木块用来补偿小车运动过程中受到的阻力，故$\rm A$错误；

$\rm B$．根据$(M+m)g\sin\theta=\mu (M+m)g\cos \theta$

解得$g\sin \theta=\mu g\cos \theta$

小车内要装钩码以增大小车质量，不需重新补偿阻力，只要保证倾角$\theta$不变即可，故$\rm B$错误；

$\rm C$．调节定滑轮的高度，使牵引小车的细线与木板平行，故$\rm C$正确；

$\rm D$．操作中，若先释放小车再接通电源，得到的纸带若点迹足够多，可以用该纸带求小车的速度和加速度，故$\rm D$错误。

故选：$\rm C$。

某次操作得到了一条纸带如图$2$所示，纸带上各相邻计数点间均有四个点迹，电源频率为$50\;\rm Hz$。根据纸带上所给的数据，计时器在打下计数点$C$时小车的速度大小$v_{C}=$                 $\;\rm m/s$，小车的加速度大小$a=$                 $\;\rm m/s^{2}$。（计算结果均保留两位有效数字）。若小车质量为$M$，槽码质量为$m$，则此条纸带的结果                 （填“能”或“不能”）用$a=\dfrac{mg}{M}$验证实验结论。

计数点之间的时间间隔为$T= \dfrac{1}{50} \times 5\;\rm \text{s}=0.1\;\rm \text{s}$

计时器在打下计数点$C$时小车的速度大小为$v_{C}=\dfrac{(4.35+6.33) \times 10^{- 2}}{0.1 \times 2}\ \text{m/s}=0.53\;\rm \text{m/s}$

小车的加速度大小为$a=\dfrac{\left( 8.34+6.33 \right) \times 10^{- 2}-\left( 4.35+2.33 \right) \times 10^{- 2}}{{0.2}^{2}}\;\rm \text{m/s}^{2}=2.0\;\rm \text{m/s}^{2}$

根据牛顿第二定律得$mg=(M+m)a$

解得$a=\dfrac{mg}{M+m}$，不能用$a=\dfrac{mg}{M}$验证实验结论。

保持槽码质量（远远小于小车和钩码总质量）不变，多次改变小车上钩码的质量，测得多组加速度$a$及对应小车上钩码的质量$m$，作出$\dfrac{1}{a}- m$图像如图$3$所示，图中直线的斜率为$k$，纵轴上的截距为$p$，若满足牛顿第二定律，则小车的质量为                 （用$p$、$k$字母表示）。

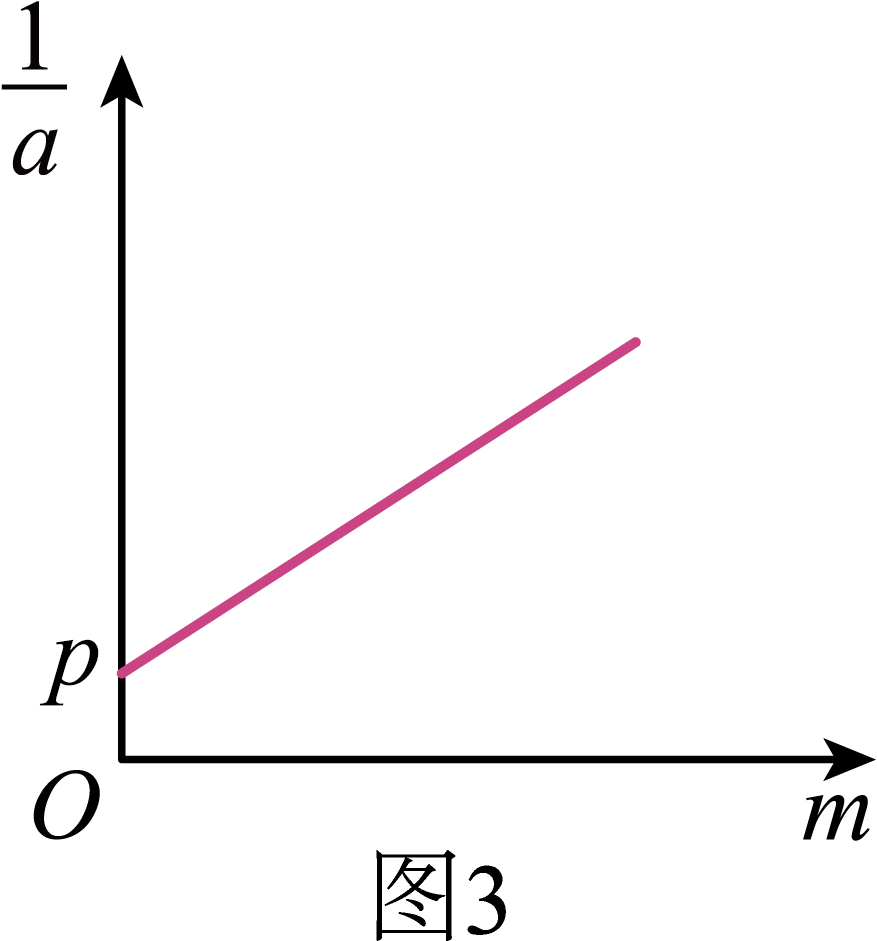
设槽码质量为$m_{0}$，根据牛顿第二定律得$m_{0}g=(m_{0}+M+m)a$

解得$\dfrac{1}{a}=\dfrac{1}{m_{0}g}m+\dfrac{m_{0}+M}{m_{0}g}$

斜率为$k=\dfrac{1}{m_{0}g}$，截距为$p=\dfrac{m_{0}+M}{m_{0}g}$

解得$M=\dfrac{p}{k}-\dfrac{1}{kg}$