高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
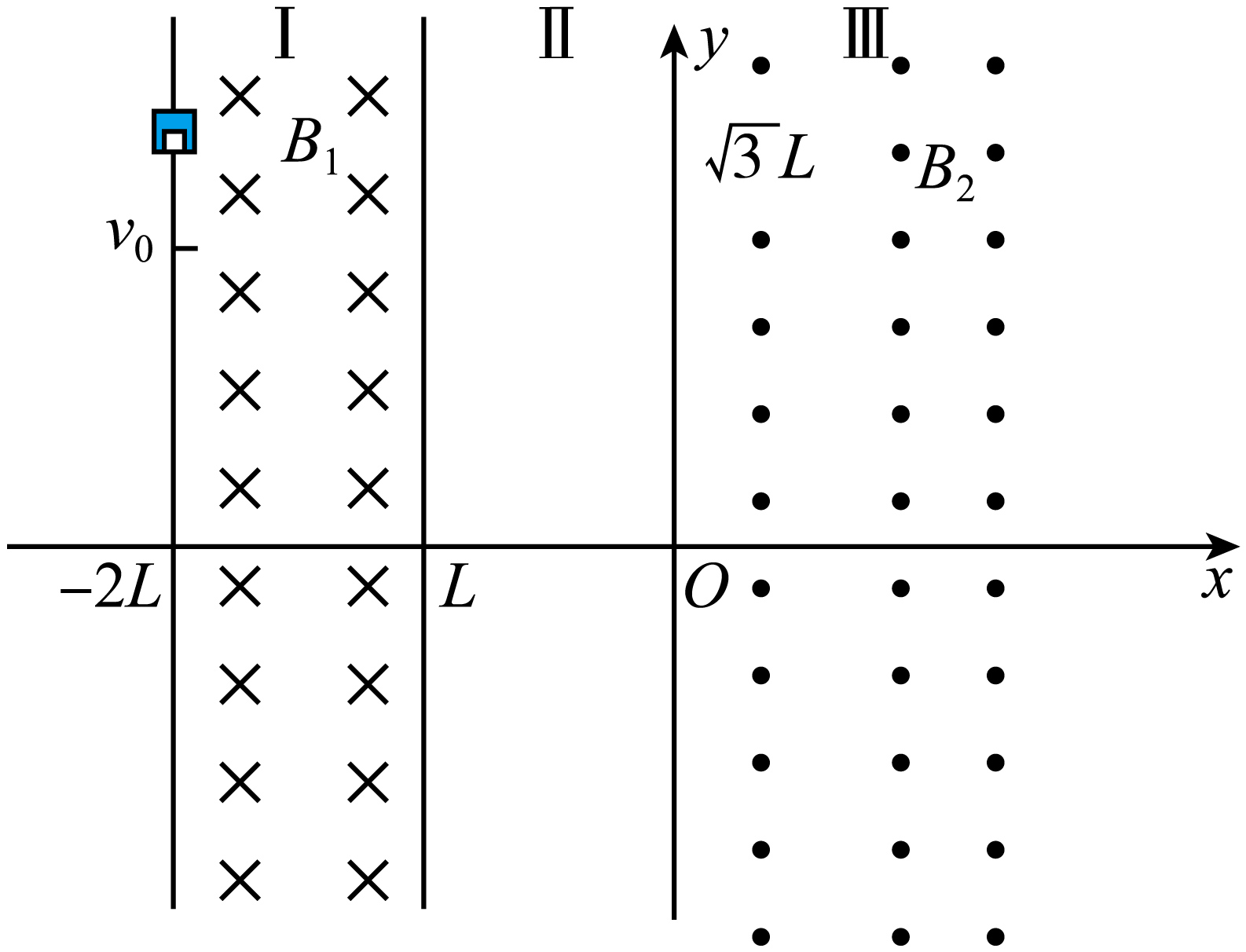
$\rm _{9}^{18}F$是正电子发射断层扫描($\rm PET$)中最重要的放射性示踪剂基础,$\rm _{9}^{18}F$发生$\beta^{*}$衰变释放出正电子$\rm (_{1}^{0}e)$,正电子湮灭产生的伽马射线用于医学成像。如图所示,在平面直角坐标系$xoy$的有三个区域,$-2L\leqslant x\lt −L$的区域Ⅰ内存在垂直纸面向里的匀强磁场$B_{1}$,在$−L\lt x\lt 0$区域Ⅱ有平行于纸面的匀强电场,大小、方向均未知,在$x\geqslant 0$的区域Ⅲ内有垂直纸面向外的匀强磁场$B_{2}$。且$B_{2}=k\pi$($k$为大于$0$的常数)。内部装有放射性元素$\rm _{9}^{18}F$的放射源放置在$\left(-2L,\sqrt{3}L \right)$处,某时刻$\rm _{9}^{18}F$发生$\beta^{*}$衰变产生的质量为$m$、带电量为$e$的正电子沿$y$轴负方向以速度大小为$v_{0}$开始运动,一段时间后从$(-L,0)$点离开磁场进入区域Ⅱ,粒子在电场中运动时间$t=\dfrac{2\sqrt{3}L}{3v_{0}}$后,从坐标原点进入区域Ⅲ,不计重力和阻力,忽略粒子之间的相互作用。
写出放射性元素$\rm _{9}^{18}F$发生$\beta^{*}$衰变的方程式;
$\\rm _{9}^{18}F →{_{8}^{18}O}+{_{1}^{0}e}$
"]]根据题意可知,衰变方程为$\rm _{9}^{18}F →{ _{8}^{18}O}+{_{1}^{0}e}$
求区域Ⅰ内匀强磁场的磁感应强度$B_{1}$的大小;
$B_{1}=\\dfrac{mv_{0}}{2eL}$
"]]正电子在磁场中运动轨迹如图所示
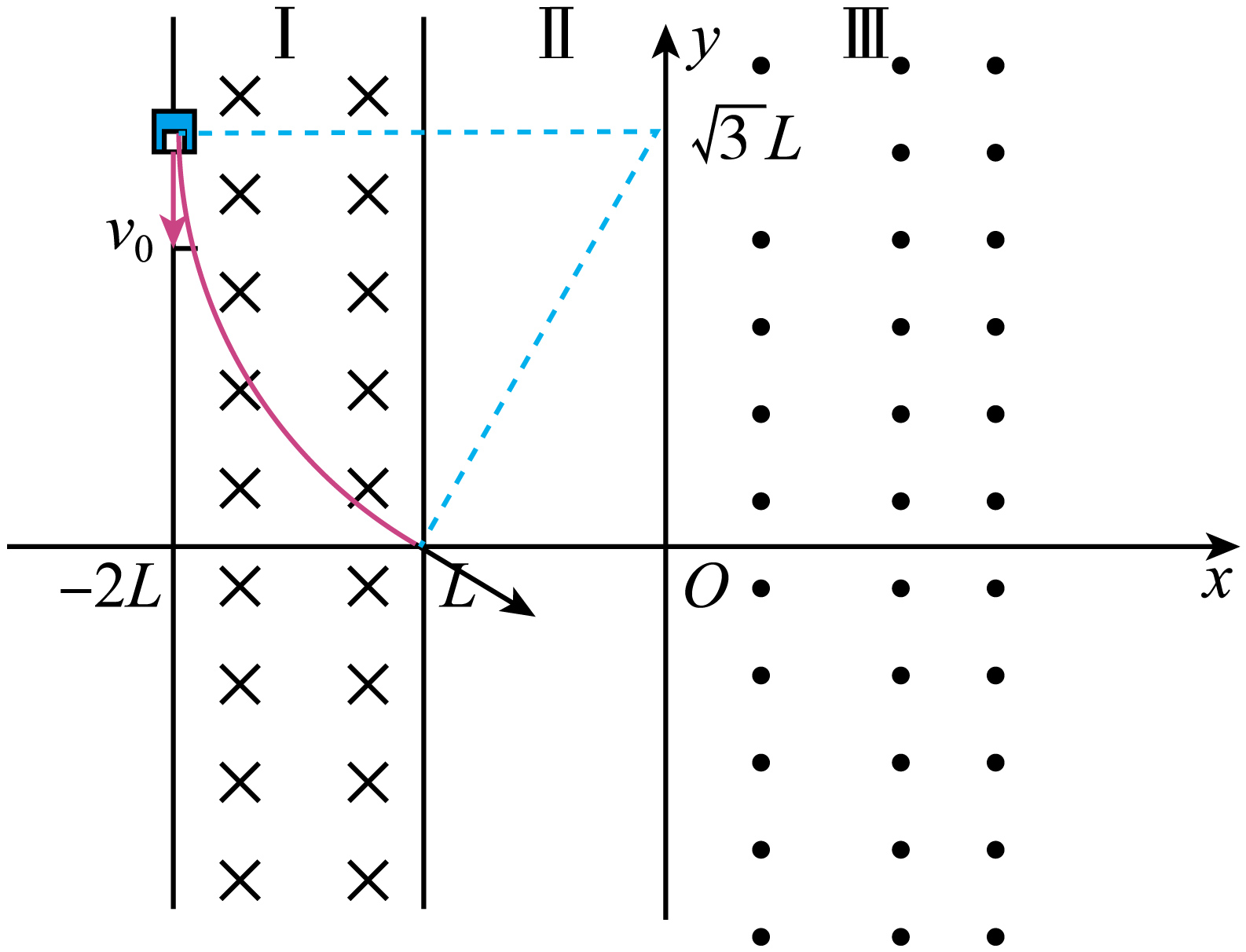
由几何关系可知$R=2L$
又根据洛伦兹力提供向心力$ev_{0}B_{1}=m\dfrac{v_{0}^{2}}{R}$
解得$B_{1}=\dfrac{mv_{0}}{2eL}$
求区域Ⅱ内匀强电场的电场强度大小及方向;
$E= \\dfrac{\\sqrt{3}mv_{0}^{2}}{2eL}$,方向沿$y$轴正方向
"]]设区域Ⅱ内的匀强电场的电场强度为$E$,根据($2$)可知粒子进入区域Ⅱ时速度与$x$轴成$30^\circ $夹角。又$y$轴方向粒子做匀变速直线运动回到$x$轴,则有$t=\dfrac{2v_{y}}{a_{y}}= \dfrac{2v_{0}\sin30{^\circ}}{a_{y}}$
其中,根据牛顿第二定律可得$a_{y}=\dfrac{eE_{y}}{m}$
联立求得$E_{y}=\dfrac{\sqrt{3}mv_{0}^{2}}{2eL}$
$x$轴方向粒子做匀变速直线运动,则有$L=v_{x}t+\dfrac{1}{2}a_{x}t^{2}=v_{0}\cos30{^\circ}t+\dfrac{1}{2}\dfrac{eE_{x}}{m}t^{2}$
解得$E_{x}=0$
综上:电场强度$E=E_{y}=\dfrac{\sqrt{3}mv_{0}^{2}}{2eL}$,方向沿$y$轴正方向。
正电子离开原点后离开$y$轴的最大距离。
$x= \\sqrt{\\dfrac{mv_{0}}{ek}}$
"]]粒子在区域Ⅱ中沿$x$轴做匀速直线运动,沿$y$轴做匀变速直线运动,到达$O$点$y$轴方向瞬时速度大小不变,所以离开$O$点瞬间速度大小为$v_{0}$,方向与$x$轴成$30^\circ $夹角斜向上。粒子在区域Ⅲ运动过程中,当粒子与$y$轴距离最大时,粒子沿$x$轴的瞬时速度为$0$,沿$y$轴速度为$v_{0}$,在$y$轴方向列动量定理$∑qB_{2}v_{x}\Delta t=mv_{0} − mv_{0}\sin30^\circ $,$\sum qB_{2}v_{x}\Delta t=q\sum B_{2}\Delta x= m\dfrac{v_{0}}{2}$
解得$x=\sqrt{\dfrac{mv_{0}}{ek}}$
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
