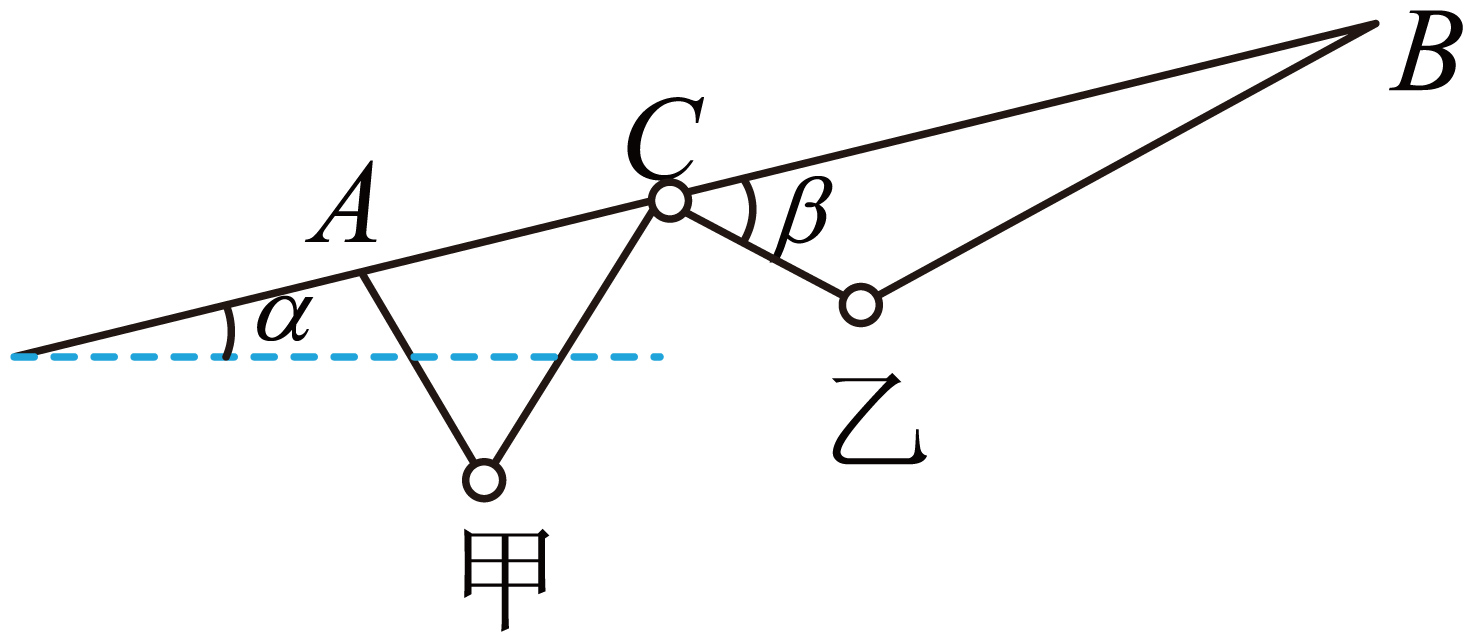
如图所示，一固定的细直杆与水平面的夹角为$\alpha=15^\circ$，一个质量忽略不计的小轻环$C$套在直杆上，一根轻质细线的两端分别固定于直杆上的$A$、$B$两点，细线依次穿过小环甲、小轻环$C$和小环乙，且小环甲和小环乙分居在小轻环$C$的两侧。调节$A$、$B$间细线的长度，当系统处于静止状态时$\beta=45^\circ$。不计一切摩擦。设小环甲的质量为$m_{1}$，小环乙的质量为$m_{2}$，则$m_{1}:m_{2}$等于$(\qquad)$

$\\tan15^\\circ$

$\\tan30^\\circ$

$\\tan60^\\circ$

$\\tan75^\\circ$

小球$C$为轻环，重力不计，受两边细线的拉力的合力与杆垂直，$C$环与乙环的连线与竖直方向的夹角为$60^\circ $，$C$环与甲环的连线与竖直方向的夹角为$30^\circ $，$A$点与甲环的连线与竖直方向的夹角为$30^\circ $，乙环与$B$点的连线与竖直方向的夹角为$60^\circ $，根据平衡条件，对甲环有$2T\cos 30^\circ =m_{1}g$

对乙环有$2T\cos 60^\circ =m_{2}g$

得$m_{1}:m_{2}=\tan 60^\circ $

故选：$\rm C$。