| 运动的合成与分解 题目答案及解析
稿件来源:高途
| 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
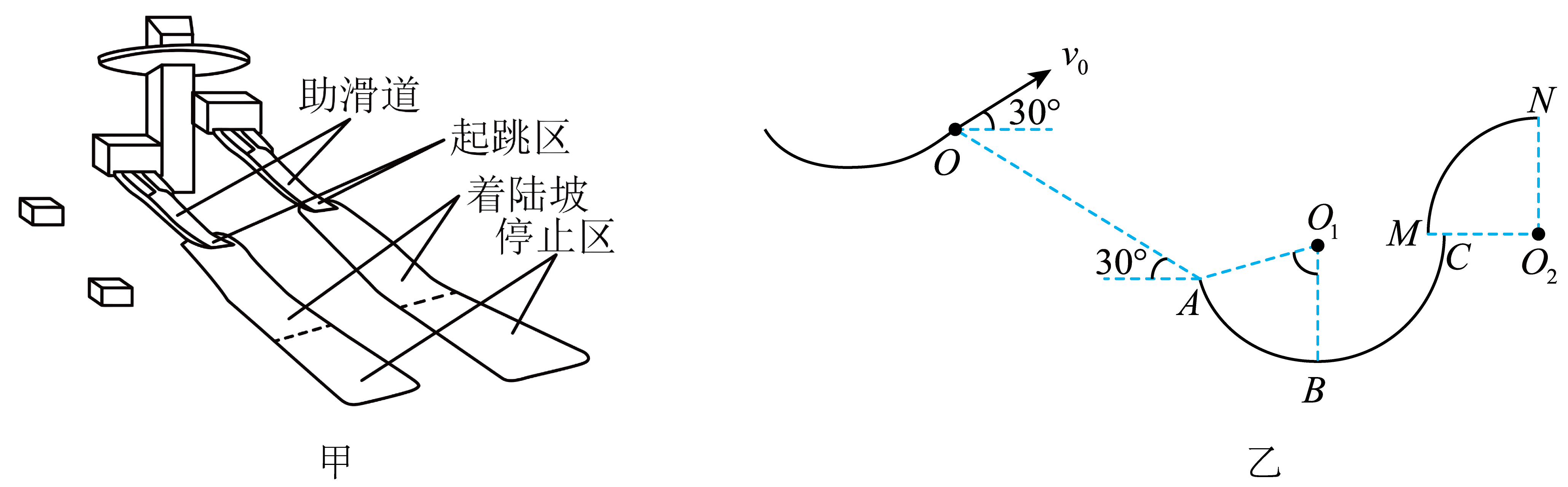
跳台滑雪是最具观赏性的运动项目之一,滑雪大跳台的赛道主要由助滑道、起跳区、着陆坡、停止区组成,其场地可以简化为如图甲所示的模型。某实验小组结合滑雪轨道设计了如图乙所示的轨道进行研究,竖直圆弧轨道$ABC$的圆心为$O_{1}$,$B$点为轨道最低点,$MN$为另一四分之一竖直圆弧轨道,圆心为$O_{2}$,圆弧轨道$ABC$和$MN$的半径相同,$C$、$M$交接处留有可供小球通过的窄缝。$O_{1}$、$M$、$C$、$O_{2}$四点在同一水平线上,$OA$两点连线与水平方向夹角为$30^\circ $。一质量$m=1\;\rm kg$的小球以与水平方向成$30^\circ $的初速度从$O$点滑出,从此时开始计时,$t=2\;\rm s$时小球离$OA$连线最远,最后恰好沿切线方向从$A$点落入圆弧轨道,已知$g=10\;\rm m/s^{2}$。求:
小球从$O$点滑出时的初速度大小;
$20\\;\\rm m/s$
"]]建立坐标系,如图
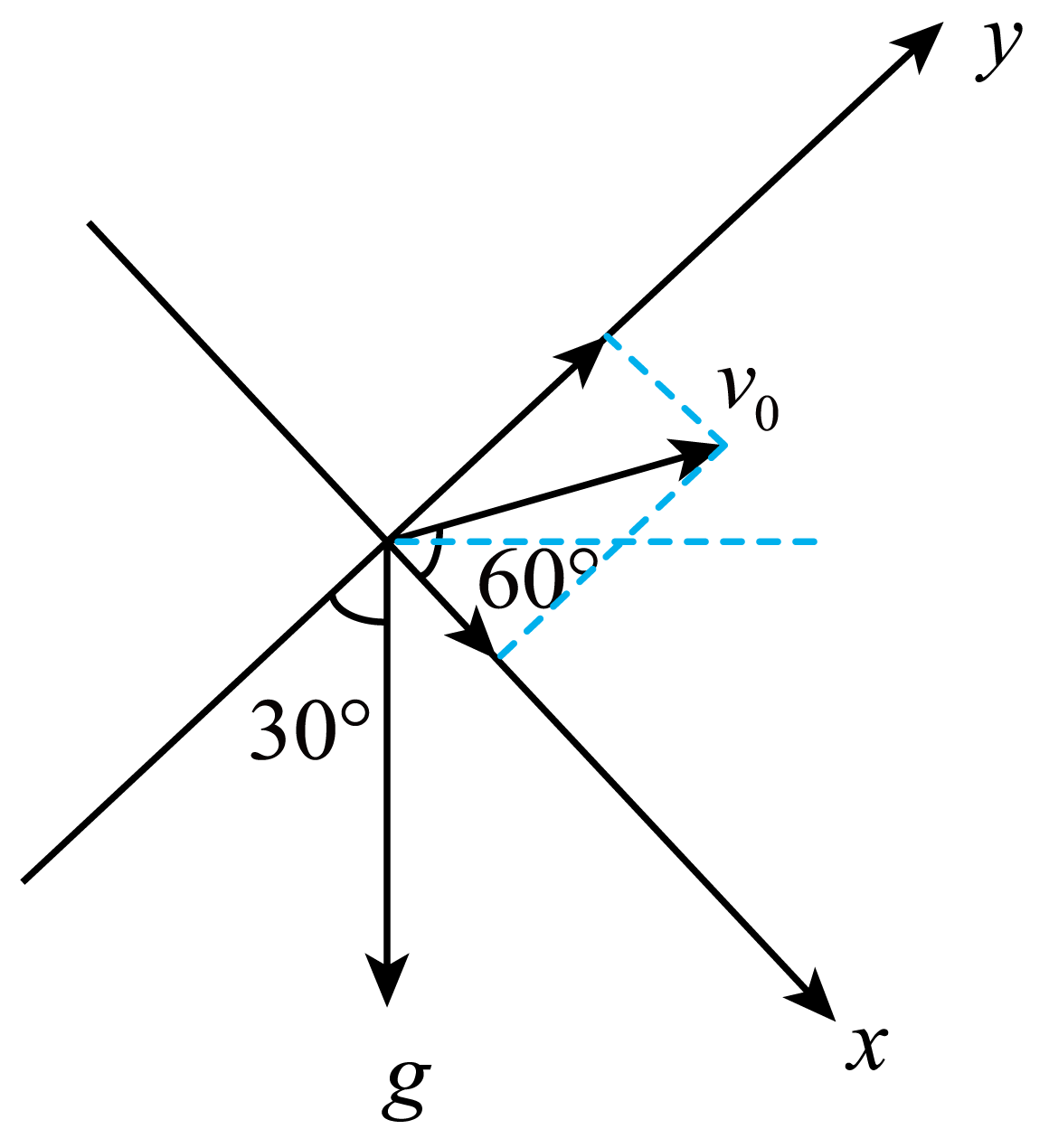
依题意,$t=2\;\rm s$时小球离$OA$连线最远,则$v_{y}=v_{0}\sin 60^\circ-g\cos 30^\circ ⋅ t=0$
解得$v_{0}=20\;\rm m/s$
$∠AO_{1}B$的正切值;
$\\sqrt{3}$
"]]小球到达$A$点,分解速度,如图
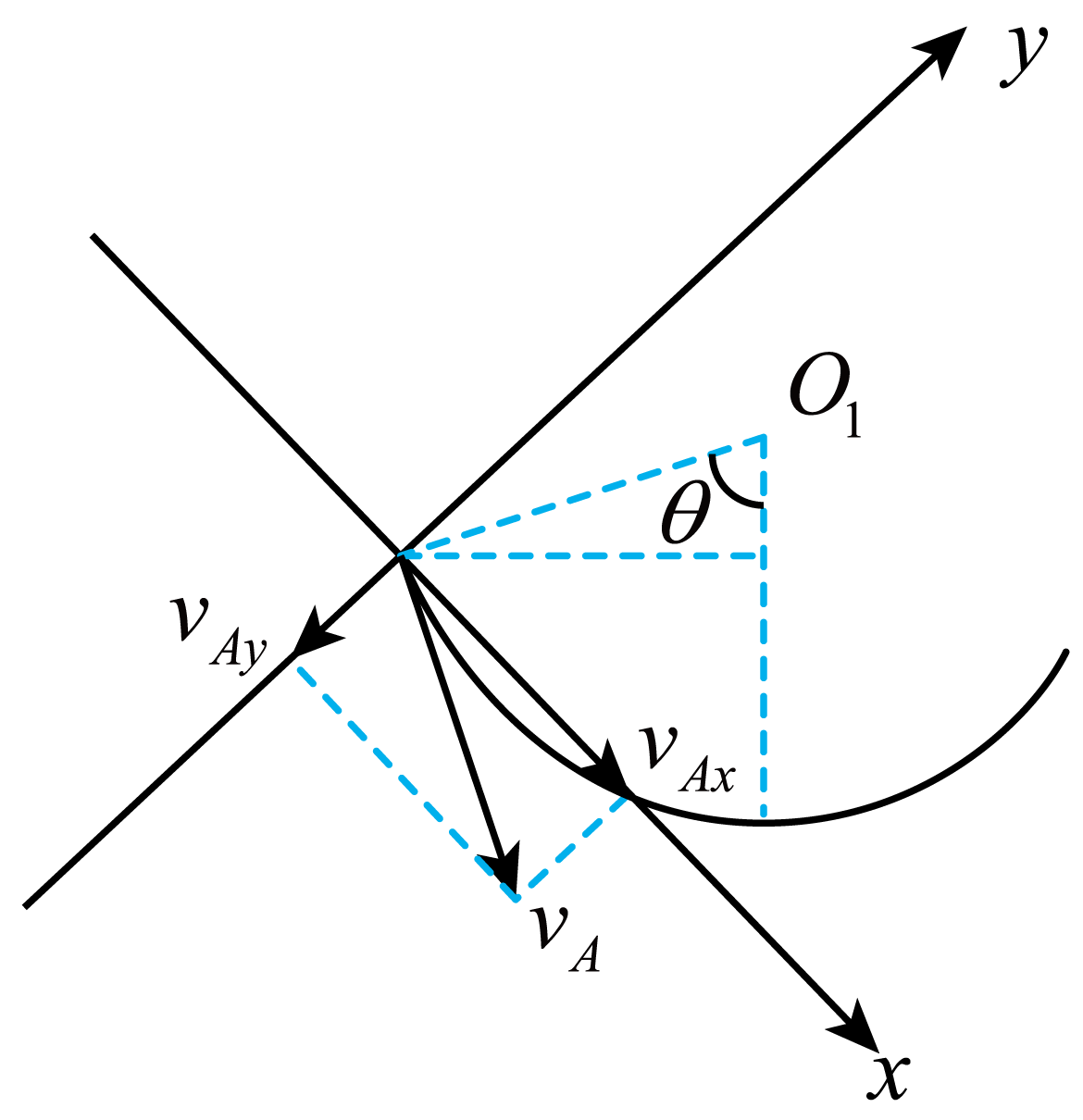
有$y=v_{0}\sin 60{^\circ} \cdot t_{1}-\dfrac{1}{2}g\cos 30{^\circ} \cdot t_{1}^{2}=0$
解得$t_{1}=4\;\rm s$
可知$v_{Ay}=v_{0}\sin 60{^\circ}-g\cos 30{^\circ} \cdot t_{1}=- 10\sqrt{3}\;\rm \text{m}/\text{s}$
$v_{Ax}=v_{0}\cos 60^\circ +g\sin 30^\circ ⋅ t_{1}=30\;\rm m/s$
由几何知识,可得$\tan(\theta-30{^\circ})=\dfrac{\left| v_{Ay} \right|}{v_{Ax}}=\dfrac{\sqrt{3}}{3}$
解得$\theta=60^\circ $
可得$\tan\theta=\sqrt{3}$
圆弧轨道$ABC$和$MN$的半径$R=48\;\rm m$时,小球脱离$MN$轨道时重力的瞬时功率。
$- 60\\sqrt{5}\\;\\rm \\text{W}$
"]]由第二问分析,可得$v_{A}=\sqrt{v_{Ay}^{2}+v_{Ax}^{2}}=20\sqrt{3}\;\rm \text{m}/\text{s}$
如图,设夹角为$\alpha$时,小球脱离$MN$轨道,
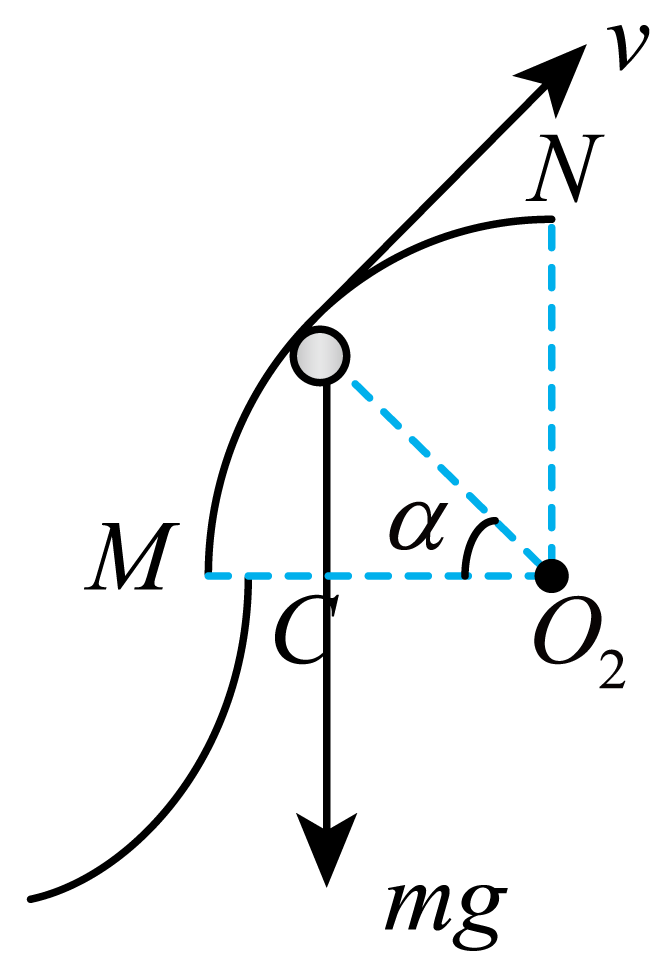
则有$mg\sin\alpha=m\dfrac{v^{2}}{R}$
由动能定理,可得$- mg\left( R\cos 60{^\circ}+R\sin\alpha \right)=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{A}^{2}$
解得$\alpha=30^\circ $,$v=4\sqrt{15}\;\rm \text{m}/\text{s}$
小球脱离$MN$轨道时重力的瞬时功率$P_{\text{G}}=mgv\cos(90{^\circ}+90{^\circ}-\alpha)=- 60\sqrt{5}\;\rm \text{W}$
| 运动的合成与分解题目答案及解析(完整版)
