| 杂化轨道理论 题目答案及解析
稿件来源:高途
| 杂化轨道理论题目答案及解析如下,仅供参考!
选修三
第二章 分子结构与性质
第二节 分子的立体结构
杂化轨道理论
钙钛矿太阳能电池是一种具有广阔应用前景的新型光伏技术。科研人员通过$\rm N-$甲基$\rm -2-$吡咯烷酮$\rm (NMP)$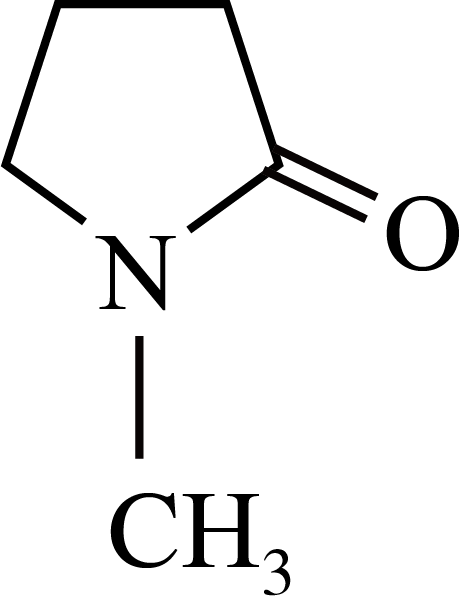 和二苯基亚砜$\rm (DPSO)$
和二苯基亚砜$\rm (DPSO)$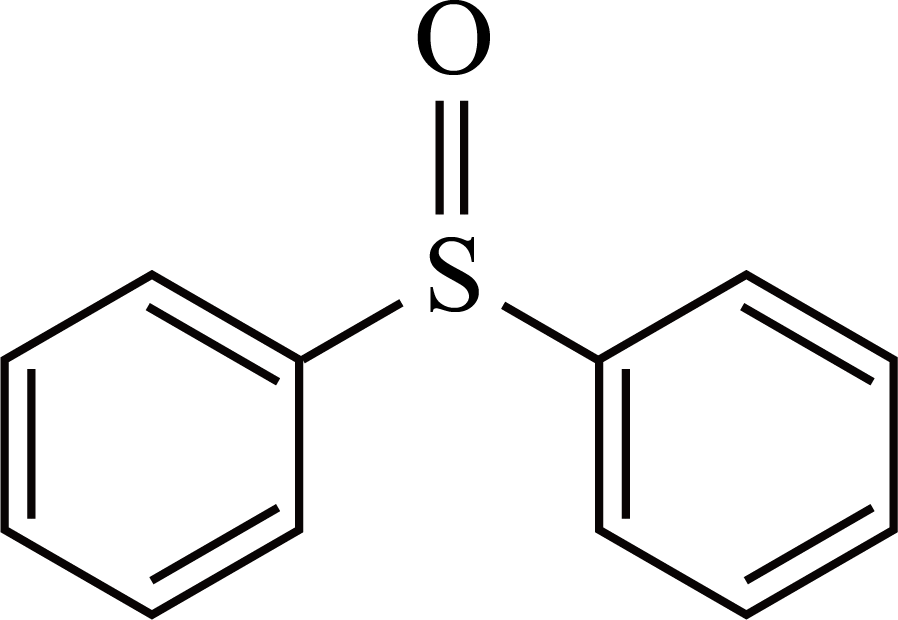 协同作用,成功制备了大面积高质量钙钛矿薄膜。
协同作用,成功制备了大面积高质量钙钛矿薄膜。
回答下列问题:
$\text{Ti}$元素在元素周期表中位于第 周期 族。
四; $\\rm IVB$
"]]$\text{Ti}$是$\rm 22$号元素,在元素周期表中位于第四周期Ⅳ$\rm B$族。
$\rm N-$甲基$\rm -2-$吡咯烷酮$\rm (NMP)$易溶于水,主要原因是 ,其中所含$\rm C$、$\rm N$、$\rm O$元素的第一电离能由大到小的顺序是 。
$\\rm NMP$能够与水形成分子间氢键 ;$\\rm N\\gt O\\gt C$
"]]$\rm NMP$能够与水形成分子间氢键,所以$\rm N-$甲基$\rm -2-$吡咯烷酮$\rm (NMP)$易溶于水;同周期元素从左到右第一电离能有增大趋势,$\rm N$原子$\rm 2p$能级半充满,结构稳定,第一电离能大于同周期相邻元素,所以$\rm C$、$\rm N$、$\rm O$元素的第一电离能由大到小的顺序是$\rm N\gt O\gt C$。
二苯基亚砜$\rm (DPSO)$分子中$\rm S$原子的杂化类型为 ,二苯基亚砜$\rm (DPSO)$作为配体时,配位原子可能是 。
$\\text{s}{{\\text{p}}^{\\text{3}}}$; $\\rm O$、$\\rm S($或氧、硫$\\rm )$
"]]二苯基亚砜$\rm (DPSO)$分子中$\rm S$原子形成$\rm 4$个共价键,其中$\rm 3$个$\rm \sigma$键,有$\rm 1$个孤电子对,杂化类型为$\text{s}{{\text{p}}^{\text{3}}}$;二苯基亚砜$\rm (DPSO)$分子中$\rm S$、$\rm O$原子都含有孤电子对,二苯基亚砜$\rm (DPSO)$作为配体时,配位原子可能是$\rm O$、$\rm S$。
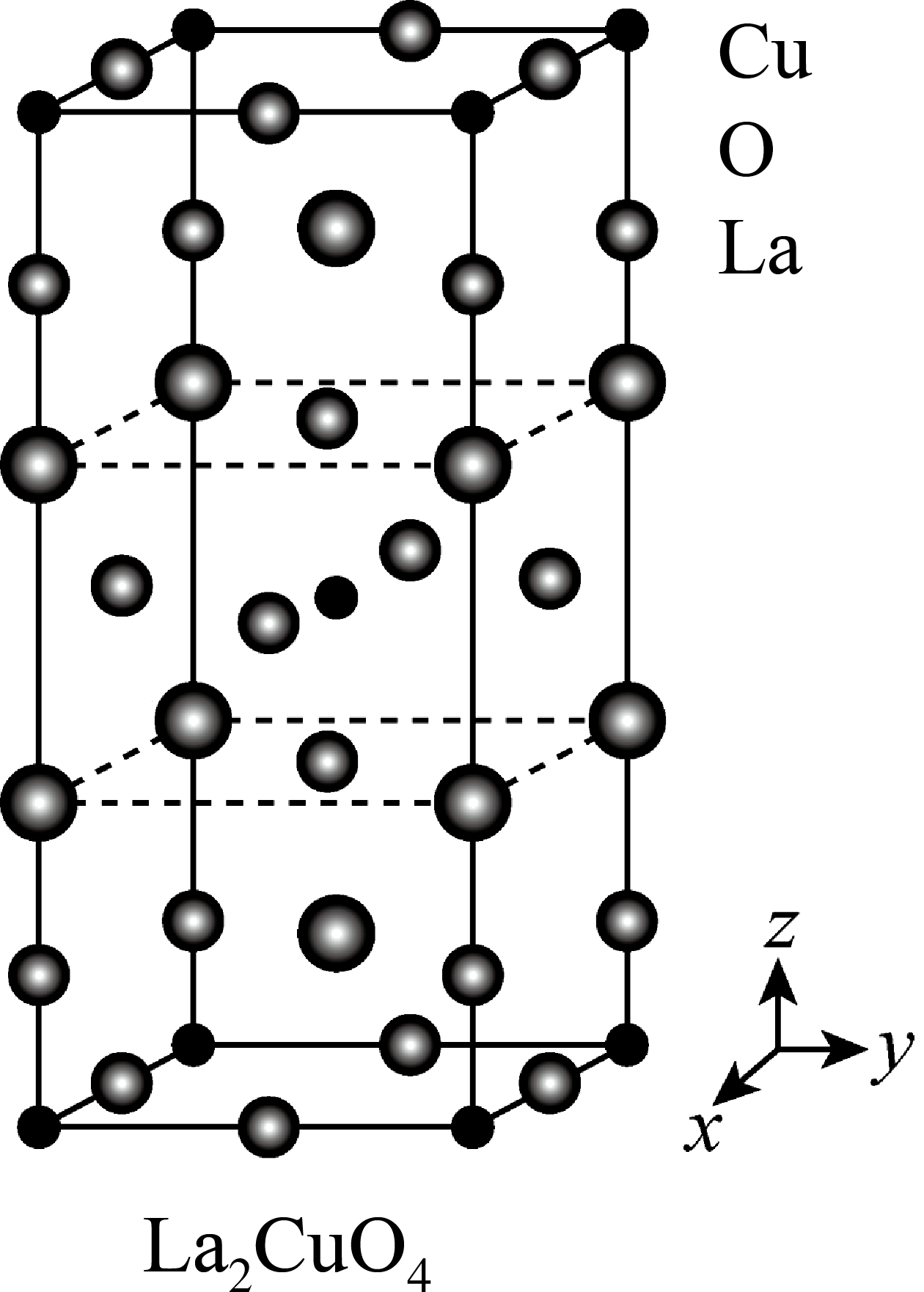
从钙钛矿结构派生出来的$\text{L}{{\text{a}}_{2}}\text{Cu}{{\text{O}}_{4}}$的晶胞结构如图所示。由于晶胞的无隙并置堆积,所以向上下左右重复,导致$\rm 8$个顶点坐标相同,都是$(0,0,0)$,所以坐标中“$\rm 1$”就是“$\rm 0$”,例如该晶胞$\text{Cu}$原子有两种不同原子坐标,$\text{La}$原子有 种不同的原子坐标。晶胞棱长分别为${a\ \rm pm}、{a\ \rm pm}、{c\ \rm pm}$,$\text{ }\!\!\alpha=\beta=\text{ }\!\!\gamma=90{}^\circ $,$\text{L}{{\text{a}}_{2}}\text{Cu}{{\text{O}}_{4}}$的摩尔质量为$\text{Mg/mol}$,求该晶体的密度$\text{ }\!\!\rho=$ $\text{g}\cdot \text{c}{{\text{m}}^{-3}}\rm ($列出计算式,设${{{N}}_{\text{A}}}$为阿伏加德罗常数的值$\rm )$。
$\\rm 4$ ;$\\dfrac{{2M}}{{{{N}}_{\\text{A}}}{{{a}}^{\\text{2}}}{c}\\times {{10}^{-30}}}$
"]]$\text{La}$原子有$\left( 0,0,\dfrac{1}{3} \right)、\left( 0,0,\dfrac{2}{3} \right)、\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{1}{6} \right)、\left( \dfrac{1}{2},\dfrac{1}{2},\dfrac{5}{6} \right)$共$\rm 4$种不同的原子坐标。晶胞棱长分别为${a\ \rm pm}、{a\ \rm pm}、{c\ \rm pm}$,$\text{ }\!\!\alpha=\beta=\text{ }\!\!\gamma=90{}^\circ $,根据均摊原则,晶胞中$\rm Cu$原子数为$8\times \dfrac{1}{8}+1=2$ ,所以$\rm La$原子数为$\rm 4$、$\rm O$原子数为$\rm 8$,$\text{L}{{\text{a}}_{2}}\text{Cu}{{\text{O}}_{4}}$的摩尔质量为$\text{Mg/mol}$,求该晶体的密度$\text{ }\!\!\rho\!\!\text{ }=\dfrac{2{M}}{{{{a}}^{\text{2}}}{p}\times {{10}^{-30}}\times {{N}_{\text{A}}}}\text{g}\cdot \text{c}{{\text{m}}^{-3}}$。
| 杂化轨道理论题目答案及解析(完整版)
