基态$\rm Ga$原子的价层电子排布式为                。

$\\text{4}{{\\text{s}}^{\\text{2}}}\\text{4}{{\\text{p}}^{\\text{1}}}$

$\rm Ga$的原子序数为$\rm 31$，核外电子数为$\rm 31$，基态原子电子排布式为：$\text{1}{{\text{s}}^{\text{2}}}\text{2}{{\text{s}}^{\text{2}}}\text{2}{{\text{p}}^{\text{6}}}\text{3}{{\text{s}}^{\text{2}}}\text{3}{{\text{p}}^{\text{6}}}\text{3}{{\text{d}}^{\text{10}}}\text{4}{{\text{s}}^{\text{2}}}\text{4}{{\text{p}}^{\text{1}}}$，则价层电子排布式为$\text{4}{{\text{s}}^{\text{2}}}\text{4}{{\text{p}}^{\text{1}}}$；

$\rm AlN$与$\rm GaN$中，$\rm N$原子的杂化方式为                ，由此推测在两种晶体中，均存在配位键。以$\rm AlN$为例，说明$\rm Al$与$\rm N$原子间可形成配位键的原因：                。

$\\text{s}{{\\text{p}}^{3}}$；铝原子可以提供空轨道，氮原子提供孤电子对，所以$\\rm Al$与$\\rm N$原子间可以形成配位键

金刚石中每个$\rm C$原子形成$\rm 4$个共价键，$\rm C$原子无孤电子对，$\rm C$原子的价层电子对数为$\rm 4$，$\rm C$原子均采取$\rm sp^{3}$杂化，由于$\rm AlN$、$\rm GaN$与金刚石结构相似，晶体中只存在$\rm N-Al$键、$\rm N-Ga$键，则$\rm N$原子的杂化方式为$\rm sp^{3}$；以$\rm AlN$为例，$\rm Al$与$\rm N$原子间可形成配位键的原因是：铝原子可以提供空轨道，氮原子提供孤电子对，故$\rm Al$与$\rm N$原子间可形成配位键；

硅是传统半导体材料，晶体硅与金刚石结构相似，但二者性质有所差异。解释金刚石硬度大于晶体硅的原因：                。

原子半径$\\rm C\\lt Si$，$\\text{C}-\\text{C}$键比$\\text{Si}-\\text{Si}$键键长短，键能大

晶体硅与金刚石结构相似，二者都属于共价晶体，金刚石硬度大于晶体硅的原因是：原子半径$\rm C\lt Si$，$\text{C}-\text{C}$键比$\text{Si}-\text{Si}$键键长短，键能大，故金刚石硬度大于晶体硅；

以$\text{C}{{\text{u}}_{2}}\text{O}$、$\rm ZnO$等半导体材料制作的传感器和芯片具有能耗低、效率高的优势。

$\rm Cu$、$\rm Zn$等金属能导电的原因是                。铜的焰色是绿色，产生此焰色时属于                $\rm ($填“发射”或“吸收”$\rm )$光谱。

金属结构中存在自由电子，自由电子在外加电场中作定向移动，故金属具有良好的导电性；发射

$\rm Cu$、$\rm Zn$等金属能导电的原因是$\rm Cu$、$\rm Zn$等金属结构中存在自由电子，自由电子在外加电场中作定向移动，故金属具有良好的导电性；铜的焰色是绿色的可见光，光是电子跃迁释放能量的表现形式，故产生此焰色时属于发射光谱；

$\rm ZnO$晶体中部分氧原子被氮原子替代后可改善半导体性能。推断$\rm Zn$与$\rm N$之间、$\rm Zn$与$\rm O$之间，哪种更有可能形成离子键，并简述推测的依据：                。

$\\rm Zn$与$\\rm O$更有可能形成离子键，因为$\\rm O$的电负性大于$\\rm N$，$\\rm Zn$与$\\rm O$之间电负性的差值较大

由于$\rm N$的电负性小于$\rm O$，$\rm Zn$与$\rm N$电负性的差值小于$\rm Zn$与$\rm O$电负性的差值，原子间电负性差值越大，形成离子键的可能性越大，故更有可能形成离子键的是$\rm Zn$与$\rm O$；故答案为：$\rm Zn$与$\rm O$更有可能形成离子键，因为$\rm O$的电负性大于$\rm N$，$\rm Zn$与$\rm O$之间电负性的差值较大；

$\text{C}{{\text{u}}_{2}}\text{O}$晶胞结构如图：

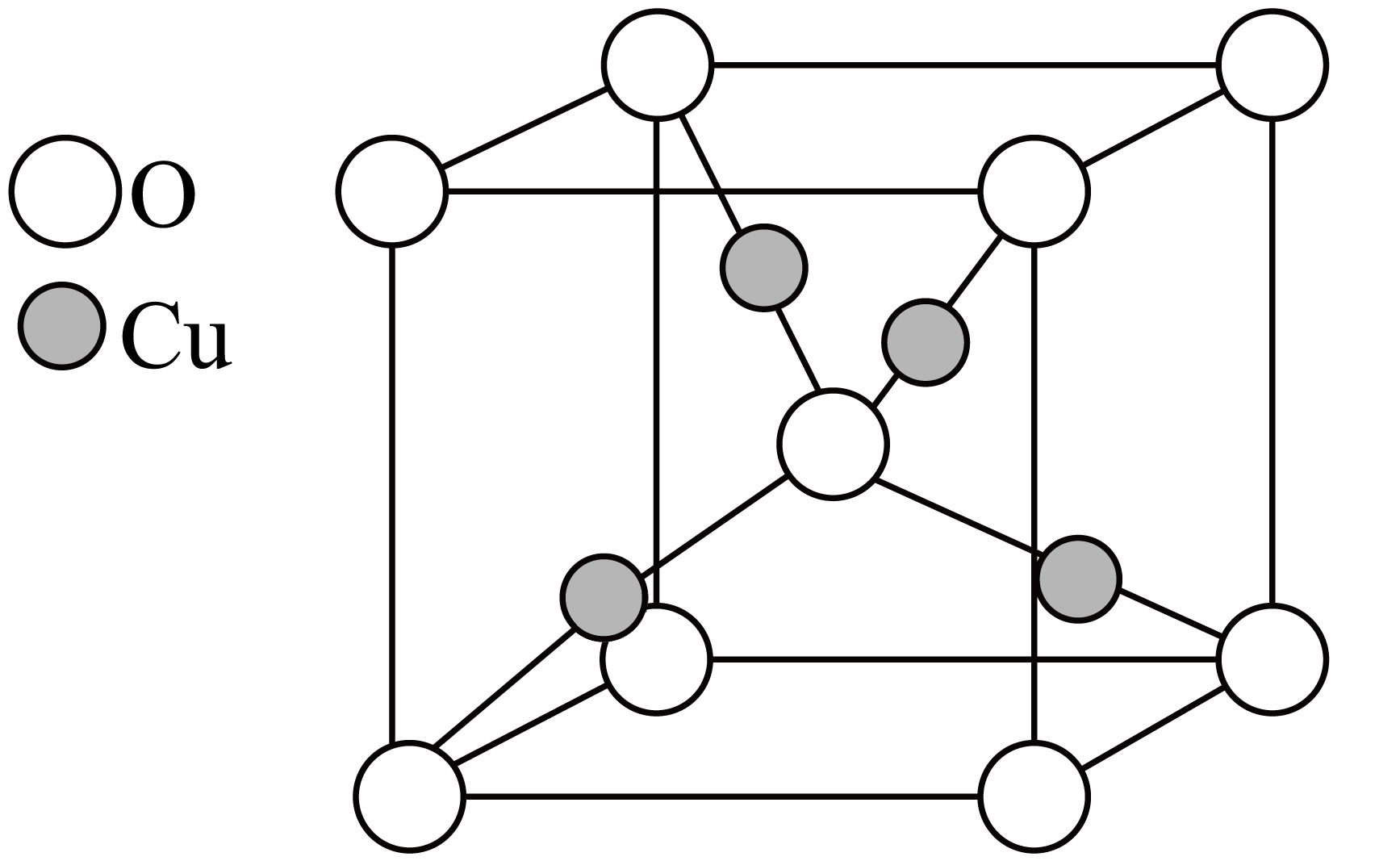
已知阿伏加德罗常数为${{ {N}}_{\text{A}}}$，最近的两个氧原子距离为$a\;\rm nm$，计算$\text{C}{{\text{u}}_{2}}\text{O}$晶体的密度为                        $\text{g}\cdot \text{c}{{\text{m}}^{\text{-3}}}$。

$\\dfrac{\\sqrt{3}\\times 1.08\\times {{10}^{23}}}{{{ {a}}^{3}}\\cdot {{ {N}}_{\\text{A}}}}$

$\rm Cu$原子位于晶胞体内有$\rm 4$个，$\rm O$原子位于晶胞顶角及体心有$8\times \dfrac{1}{8}+1=2$个，最近的两个氧原子为顶角与体心的两个$\rm O$原子，距离为$a\;\rm nm$，则晶胞参数边长为$\dfrac{2{a}}{\sqrt{3}}\;\rm{nm}$，根据$\rho =\dfrac{{n}\cdot {M}}{{V}\cdot {{{N}}_{\rm{A}}}}$计算，$\rho =\dfrac{2\times \left( 64\times 2+16 \right)}{{{\left( \dfrac{2{a}}{\sqrt{3}}\times {{10}^{-7}} \right)}^{3}}\cdot {{{N}}_{\rm{A}}}}{\;\rm{g}\cdot {c}{{{m}}^{{-3}}}}=\dfrac{\sqrt{3}\times 1.08\times {{10}^{23}}}{{{{a}}^{3}}\cdot {{{N}}_{\rm{A}}}}\rm\;{ g}\cdot {c}{{{m}}^{{-3}}}$。