恒压时，使镧镍合金“呼吸”氢气的方法是                。

升高温度

根据反应$\text{LaN}{{\text{i}}_{5}}\left( \text{s} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{LaN}{{\text{i}}_{5}}{{\text{H}}_{6}}\left( \text{s} \right)$，$\Delta H=-\text{31}\text{.77}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$为放热反应，所以恒压时，使镧镍合金“呼出”氢气的方法是即使平衡逆向移动，可升高温度；

$\rm I$$\rm I$.乙醇与水催化重整制“氢”发生如下反应。

反应$\rm I$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 2\text{CO}\left( \text{g} \right)+4{{\text{H}}_{2}}\left( \text{g} \right)$    

反应$\rm II$：$\text{CO}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{O}}_{2}}\left( \text{g} \right)+{{\text{H}}_{2}}\left( \text{g} \right)\quad \Delta {{H}_{\text{2}}}=-\text{41}\text{.2}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$    

反应$\rm III$：${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons 2\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+6{{\text{H}}_{2}}\left( \text{g} \right)\quad \Delta {{H}_{\text{3}}}=+\text{173}\text{.3}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$    

回答下列问题：

反应$\rm I$的$\Delta {{H}_{1}}\rm =$                ，该反应                $\rm ($填“高温”或“低温”或“不能”$\rm )$自发进行。

$+255.7\\,\\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$ ； 高温

根据盖斯定律，反应Ⅰ$\rm =$反应Ⅲ$\rm -2\times $反应Ⅱ，则$\Delta{{H}_{1}}=\Delta {{H}_{3}}-2\Delta {{H}_{\text{1}}}\text{=(+173}\text{.3}\,\text{kJ/mol)-2}\times \text{(-41}\text{.2}\,\text{kJ/mol})=+\text{255}\text{.7}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}$；根据$\Delta G=\Delta H-T\Delta S\lt 0$时可自发反应，$\Delta {{H}_{1}}=+\text{255}\text{.7}\,\text{kJ}\cdot \text{mo}{{\text{l}}^{\text{-1}}}\gt 0$，该反应气体分子数增大$\Delta S\gt 0$，故可在高温下自发进行；

上述反应体系在一定条件下建立平衡后，下列说法正确的有                。

$\rm A$．增大$\rm CO$浓度，反应①、②的正反应速率都增加

$\rm B$．加入反应①的催化剂，可提高$\rm {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}$的平衡转化率

$\rm C$．降低反应温度，反应①②③的正、逆反应速率都减小

$\\rm AC$

$\rm A$．增大$\rm CO$浓度，反应①生成物浓度增加，平衡逆向移动正反应速率也增加，反应②的反应物浓度增大正反应速率增加，$\rm A$正确；

$\rm B$．催化剂不影响平衡移动，不会改变$\rm {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}$的平衡转化率，$\rm B$错误；

$\rm C$．降低反应温度，单位体积内活化分子百分数减小，反应速率都减小，所以反应①②③的正、逆反应速率都减小，$\rm C$正确；

反应$\rm II$的速率$v={{v}_{正}}-{{v}_{逆}}={{k}_{正}}c\left( \text{CO} \right)\cdot c\left( {{\text{H}}_{\text{2}}}\text{O} \right)-{{k}_{逆}}c\left( \text{C}{{\text{O}}_{\text{2}}} \right)\cdot c\left( {{\text{H}}_{\text{2}}} \right)$，其中${{k}_{正}}$、${{k}_{逆}}$分别为正、逆反应速率常数。降低温度时$\text{lg}\,{{k}_{正}}\text{-lg}\,{{k}_{逆}}$                $\rm ($填“增大”“减小”或“不变”$\rm )$。

增大

达到平衡时，${{v}_{正}}={{v}_{逆}}={{k}_{正}}c\left( \text{CO} \right)\cdot c\left( {{\text{H}}_{\text{2}}}\text{O} \right)={{k}_{逆}}c\left( \text{C}{{\text{O}}_{\text{2}}} \right)\cdot c\left( {{\text{H}}_{\text{2}}} \right)$，$\text{lg}\,{{k}_{正}}-\text{lg}\,{{k}_{逆}}=\text{lg}\,\dfrac{{{k}_{正}}}{{{k}_{逆}}}=\text{lg}\dfrac{c(\text{C}{{\text{O}}_{2}})\cdot c({{\text{H}}_{\text{2}}})}{c(\text{CO})\cdot c({{\text{H}}_{\text{2}}}\text{O})}=\text{lg}\,K$，降低温度，反应Ⅱ正向移动，平衡常数增大，$\text{lg}\,K$增大；

压强为$\rm 100$ $\rm kPa$下，$\rm 1$ $\rm mol$ ${{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\rm (g)$和$\rm 3$ $\rm mol$ ${{\text{H}}_{2}}\text{O}\rm (g)$发生上述反应，平衡时$\text{C}{{\text{O}}_{2}}$和$\rm CO$的选择性、乙醇的转化率随温度的变化曲线如图。

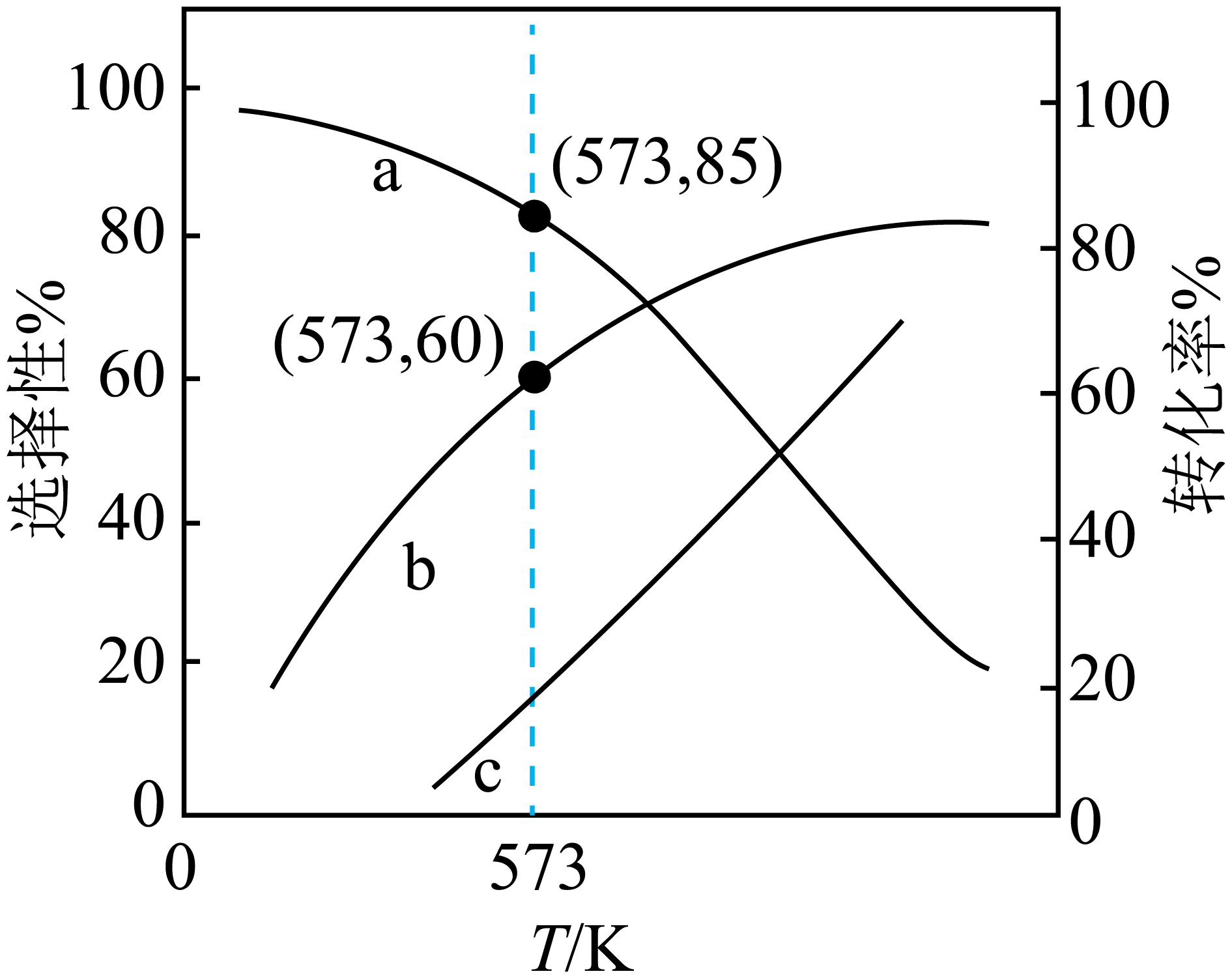
$\rm [$已知：$\rm CO$的选择性$=\dfrac{{{n}_{生成}}\left( \text{CO} \right)}{{{n}_{生成}}\left( \text{CO} \right)+{{n}_{生成}}\left( \text{C}{{\text{O}}_{\text{2}}} \right)}\rm ]$

①表示$\text{C}{{\text{O}}_{2}}$选择性的曲线是                $\rm ($填标号$\rm )$；

②$\rm 573$ $\rm K$时，生成$\rm CO$的物质的量为                ；

③反应$\rm II$的标准平衡常数${{K}^{\theta }}=\dfrac{\dfrac{p\left( \text{C}{{\text{O}}_{\text{2}}} \right)}{{{p}^{\theta }}}\times \dfrac{p\left( {{\text{H}}_{\text{2}}} \right)}{{{p}^{\theta }}}}{\dfrac{p\left( \text{CO} \right)}{{{p}^{\theta }}}\times \dfrac{p\left( {{\text{H}}_{\text{2}}}\text{O} \right)}{{{p}^{\theta }}}}$，其中${{p}^{\theta }}$为$\rm 100$ $\rm kPa$，$p\left( \text{C}{{\text{O}}_{\text{2}}} \right)$、$p\left( {{\text{H}}_{\text{2}}} \right)$、$p\left( \text{CO} \right)$和$p\left( {{\text{H}}_{\text{2}}}\text{O} \right)$为各组分的平衡分压，则反应$\rm III$的${{K}^{\theta }}=$                $\rm ($列出计算式即可$\rm )$。

$\\rm a$ ； $\\rm 0.18$ $\\rm mol$ ； $\\dfrac{{{\\left( \\dfrac{1.02}{6.4} \\right)}^{2}}\\times {{\\left( \\dfrac{3.42}{6.4} \\right)}^{6}}}{\\dfrac{0.4}{6.4}\\times {{\\left( \\dfrac{1.38}{6.4} \\right)}^{3}}}$

①反应Ⅰ、Ⅲ为吸热反应，反应Ⅱ为放热反应，随着温度的升高，反应Ⅰ、Ⅲ平衡正向移动，反应Ⅱ平衡逆向移动，反应Ⅱ逆向移动$\rm CO_{2}$转化为$\rm CO$，故温度升高$\rm CO$的选择性增大，$\rm CO_{2}$的选择性减小，由于$\rm CO$的选择性$\rm +CO_{2}$的选择性$\rm =1$，则表示$\rm CO_{2}$选择性的曲线为$\rm a$，表示$\rm CO$选择性的曲线是$\rm c$，表示乙醇的转化率的曲线是$\rm b$；

②$\rm 573$ $\rm K$时，$\rm CO_{2}$的选择性为$\rm 85\%$，$\rm CO$的选择性为$\rm 15\%$，乙醇的转化率为$\rm 0.6$，则平衡时根据碳原子守恒：$n\left( \text{C}{{\text{O}}_{\text{2}}} \right)+n\left( \text{CO} \right)=1\,\text{mol}\times 0.6\times 2=1.2\,\text{mol}$，$n\left( \text{CO} \right)=1.2\,\text{mol}\times 15\%=0.18\,\text{mol}$，$n\left( \text{C}{{\text{O}}_{\text{2}}} \right)=1.2\,\text{mol}\times 85\%=1.02\,\text{mol}$；

③设反应Ⅰ中转化了乙醇$x\,\text{mol}$，反应Ⅱ中$\rm CO$转化了$y\,\text{mol}$，反应Ⅲ中乙醇转化了$z\,\text{mol}$，则$\begin{matrix} {} & {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & 2\text{CO}\left( \text{g} \right) & + & \text{4}{{\text{H}}_{\text{2}}}\left( \text{g} \right) \\转化量 \text{/mol} & x & {} & x & {} & 2x & {} & 4x \\ \end{matrix}$，$\begin{matrix} {} & \text{CO}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\left( \text{g} \right) \\转化量 \text{/mol} & y & {} & y & {} & y & {} & y \\ \end{matrix}$，$\begin{matrix} {} & {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{OH}\left( \text{g} \right) & + & \text{3}{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) & \rightleftharpoons & \text{2C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & \text{6}{{\text{H}}_{\text{2}}}\left( \text{g} \right) \\转化量 \text{/mol} & z & {} & 3z & {} & 2z & {} & 6z \\ \end{matrix}$，那么$x+z=0.6$，$2x-y=0.18$，$y+2z=1.02$，平衡时$n\left( {{\text{H}}_{\text{2}}}\text{O} \right)=3-x-y-3z=3-\left( x+z \right)-\left( y+2z \right)=3-0.6-1.02=1.38\,\text{mol}$，$n\left( {{\text{H}}_{\text{2}}} \right)=4x+y+6z=4\left( x+z \right)+\left( y+2z \right)=2.4+1.02=3.42\,\text{mol}$，气体的总物质的量为$\rm 0.4+1.38+1.02+0.18+3.42=6.4$ $\rm mol$，故反应Ⅲ的${{K}^{\theta }}=\dfrac{{{\left( \dfrac{1.02}{6.4} \right)}^{2}}\times {{\left( \dfrac{3.42}{6.4} \right)}^{6}}}{\dfrac{0.4}{6.4}\times {{\left( \dfrac{1.38}{6.4} \right)}^{3}}}$。