一抛物线形状的光滑固定导轨竖直放置，$O$为抛物线导轨的顶点，$O$点离地面的高度为$h$，$A$、$B$两点相距$2h$，轨道上套有一个小球$M$，小球$M$通过轻杆与光滑地面上的小球$N$相连，两小球的质量均为$m$，轻杆的长度为$2h$。现将小球$M$从距地面竖直高度为$\dfrac{3}{4}h$处静止释放，下列说法正确的是$(\qquad)$

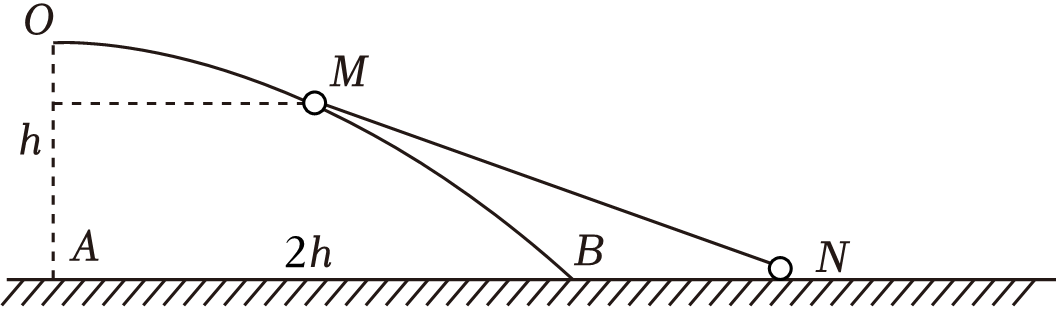
小球$M$即将落地时，它的速度方向与水平面的夹角为$30^\\circ$

小球$M$ 即将落地时，它的速度方向与水平面的夹角为$60^\\circ$

从静止释放到小球$M$即将落地，轻杆对小球$N$ 做的功为$\\dfrac{1}{4}mgh$

若小球$M$ 落地后不反弹，则地面对小球$M$ 的作用力的冲量大小为$m\\sqrt{gh}$

$\rm AB$、小球$M$ 即将落地时，它的速度方向与抛物线轨道相切，根据平抛规律的推论可知，小球$M$ 的速度方向与水平方向的夹角满足：$\tan\theta = \dfrac{h}{\dfrac{2h}{2}} = 1$

所以可得：$\theta=45^\circ$，故$\rm AB$错误；

$\rm C$、设小球 $M$ 即将落地时，速度大小为$v_{1}$，小球$N$的速度大小为 $v_{2}$，根据系统机械能守恒有$\dfrac{3}{4}mgh = \dfrac{1}{2}mv_{1}^{2} + \dfrac{1}{2}mv_{2}^{2}$

小球 $M$ 与小球 $N$沿杆方向的速度相等，有：$v_{1}\cos\theta=v_{2}$

解得：$v_{1} = \sqrt{gh},v_{2} = \sqrt{\dfrac{gh}{2}}$

根据动能定理可得，从静止释放到小球 $M$ 即将落地，轻杆对小球 $N$ 做的功为：$W_{杆} = \dfrac{1}{2}mv_{2}^{2} = \dfrac{1}{4}mgh$，故$\rm C$正确；

$\rm D$、小球 $M$ 落地与地面相互作用的过程中不反弹，以竖直向上方向为正，根据动量定理有：$I_{地}+I_{G}+I_杆+I_{轨}=0-(- m\sqrt{gh})$，由于轨道、轻杆对小球有作用力，且小球$M$ 有重力，所以|$I_{地}|\gt |I_{合}|= m\sqrt{gh}$，故$\rm D$错误。

故选：$\rm C$。