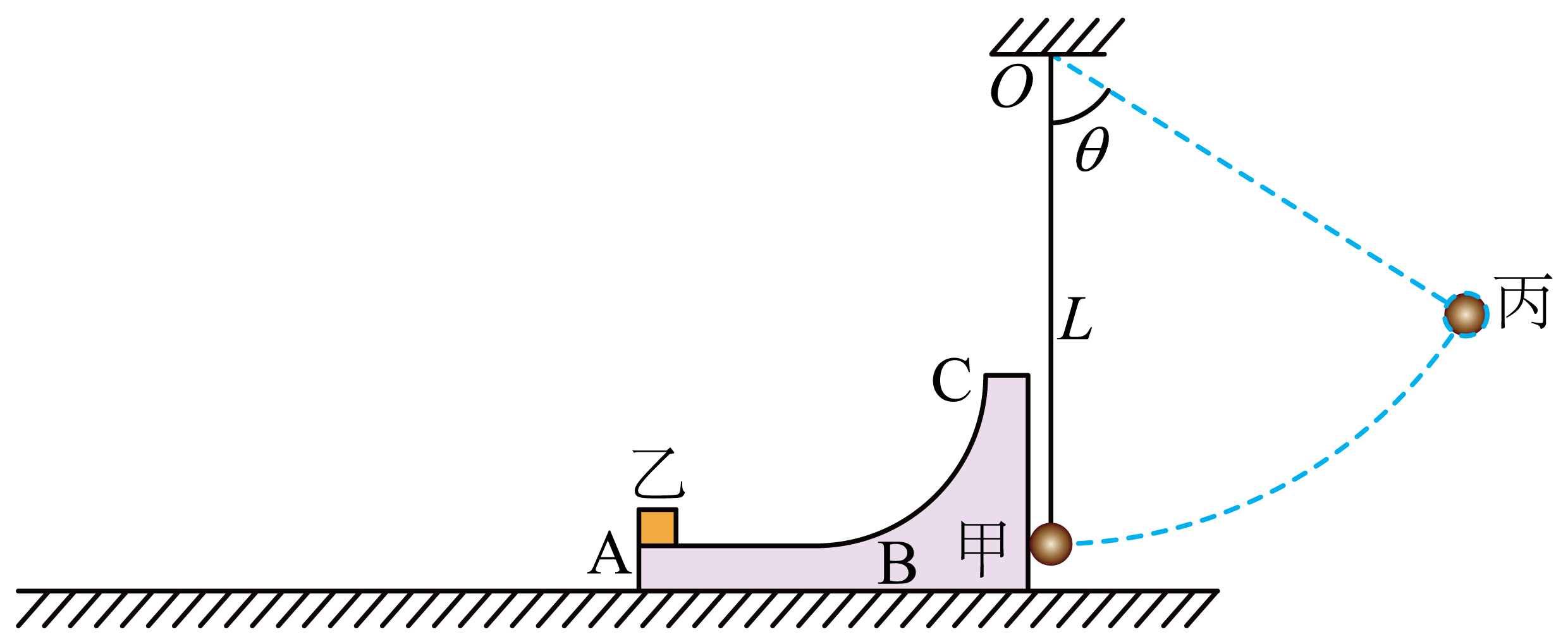
求丙与甲碰后瞬间各自速度的大小；

$2.4\\;\\rm m/s$，$6.4\\;\\rm m/s$；

丙向下摆动过程中机械能守恒$MgL\left( 1-\cos\theta \right)=\dfrac{1}{2}Mv_{0}^{2}$

解得$v_{0}=4\;\rm m/s$

丙与甲碰撞过程，由动量守恒得$Mv_{0}=Mv{^\prime}+mv$

由机械能守恒得$\dfrac{1}{2}Mv_{0}^{2}=\dfrac{1}{2}Mv{'^2}+\dfrac{1}{2}mv^{2}$

解得碰后瞬间，丙速度大小$v{^\prime}=2.4\;\rm m/s$

甲速度大小$v=6.4\;\rm m/s$

通过计算分析判断，碰后甲向左滑动的过程中，乙能否从$C$点离开圆弧轨道。

见解析

假设乙能从$C$点离开，$C$点甲、乙水平速度相同，设甲速度为$v_{甲2}$，从丙与甲碰撞结束至乙从$C$点离开甲过程，甲、乙水平方向动量守恒$mv=2mv_{甲2}$

解得$v_{甲2}=3.2\;\rm m/s$

设乙从$C$点离开时乙竖直方向速度大小为$v_{y}$，从丙与甲碰撞结束至乙从$C$点离开甲过程中，由机械能守恒得$\dfrac{1}{2}mv^{2}=\dfrac{1}{2}mv_{甲2}^{2}+\dfrac{1}{2}mv_{乙1}^{2}+mgR$

又因为$v_{乙1}^{2}=v_{甲2}^{2}+v_{y}^{2}$

解得$v_{y}=2\;\rm m/s\gt 0$

所以乙能从$C$离开圆弧轨道。