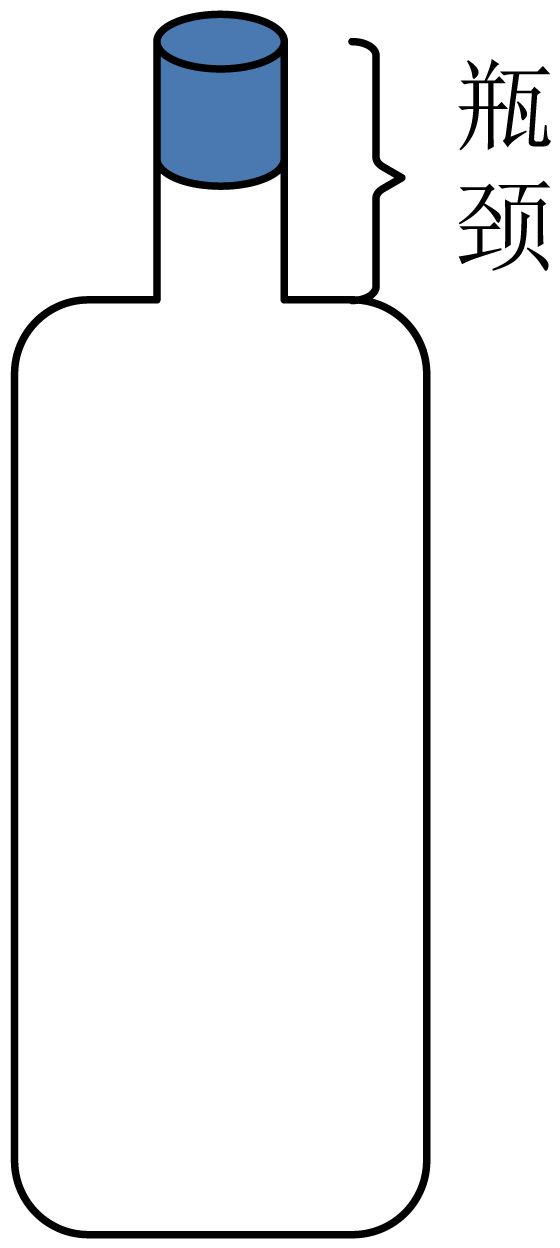
房间内室温为$300\;\rm K$，大气压强为$p_{0}$。在此房间内给一玻璃瓶充入压缩气体，用圆柱形轻质软木塞塞住横截面为圆、面积为$S$的瓶颈使瓶口密封，瓶内压缩气体的温度与室温相同，压强$p=2p_{0}$，软木塞相对于瓶颈保持静止，如图所示。再将该玻璃瓶放入温度为$77\;\rm K$的液氮中充分冷却，随后迅速放回房间，此时瓶颈与软木塞之间的静摩擦力大小为                 。若软木塞与瓶颈之间的弹力大小始终为$N$，则二者之间的静摩擦因数$\mu $满足条件                 （用题给物理量表示）时，才能使瓶颈内的软木塞一直保持不动。假设瓶子和软木塞的热胀冷缩可忽略，瓶内气体可视为理想气体。

瓶内气体发生等容变化，根据$\dfrac{p}{T_{1}}=\dfrac{p'}{T_{2}}$

可得$p'=\dfrac{T_{2}}{T_{1}}p=\dfrac{77}{150}p_{0}$

根据平衡条件可知瓶颈与软木塞之间的静摩擦力大小$f=p_{0}S-p'S=\dfrac{73}{150}p_{0}S$

随着温度降低，瓶内压强逐渐减小，可知初始状态，瓶塞所受摩擦力最大，且最大值为$f_{\rm m}=pS − p_{0}S=p_{0}S$

因此静摩擦因数$\mu $满足条件$\mu \geq \dfrac{f_{{\rm m}}}{N}=\dfrac{p_{0}S}{N}$。