方案一：用如图甲所示的装置，已知小球在挡板$A$、$B$、$C$处做圆周运动的轨迹半径之比为$1:2:1$，变速塔轮自上而下按如图乙所示三种组合方式，左右每层半径之比由上至下分别为$1:1$、$2:1$和$3:1$。回答以下问题：

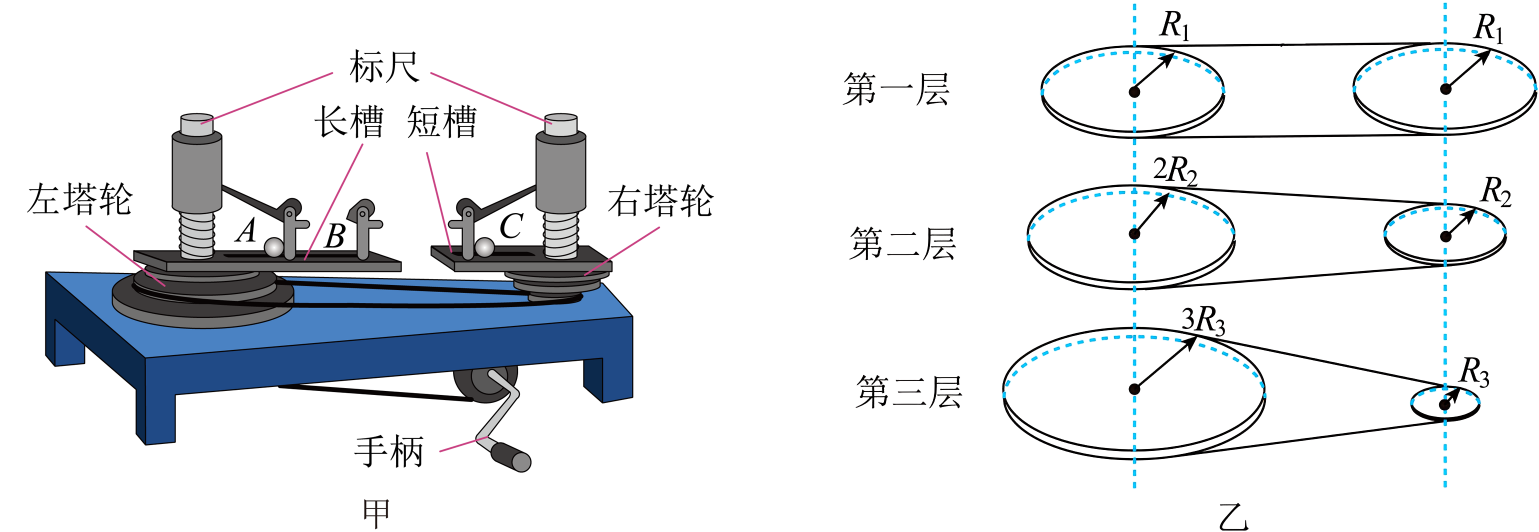
①本实验所采用的实验探究方法与下列哪些实验是相同的                ；

$\rm A$．探究小车速度随时间变化规律   $\rm B$．探究两个互成角度的力的合成规律

$\rm C$．探究平抛运动的特点   $\rm D$．探究加速度与物体受力、物体质量的关系

②某次实验中，把两个质量相等的钢球放在$B$、$C$位置，探究向心力的大小与半径的关系，则需要将传动皮带调至第                层塔轮（填“一”、“二”或“三”）。

$\\rm D$；一

在该实验中，通过控制质量、半径、角速度中两个物理量相同，探究向心力与另外一个物理量之间的关系，采用的科学方法是控制变量法。

$\rm A$．探究小车速度随时间变化规律，利用极限思想计算小车的速度，故$\rm A$错误；

$\rm B$．探究两个互成角度的力的合成规律，应用了等效替代法，故$\rm B$错误；

$\rm C$．探究平抛运动的特点，例如两球同时落地，两球在竖直方向上的运动效果相同，应用了等效思想，故$\rm C$错误；

$\rm D$．探究加速度与物体受力、物体质量的关系，应用了控制变量法，故$\rm D$正确。

故选：$\rm D$。

把两个质量相等的钢球放在$B$、$C$位置，探究向心力的大小与半径的关系，应使两球的角速度相同，则需要将传动皮带调至第一层塔轮。

方案二：如图丙所示装置，装置中竖直转轴固定在电动机的转轴上（未画出），光滑的水平直杆固定在竖直转轴上，能随竖直转轴一起转动。水平直杆的左端套上滑块$P$，用细线将滑块$P$与固定在竖直转轴上的力传感器连接，细线处于水平伸直状态，当滑块随水平直杆一起匀速转动时，细线拉力的大小可以通过力传感器测得。水平直杆的右端最边缘安装了宽度为$d$的挡光条，挡光条到竖直转轴的距离为$D$，光电门可以测出挡光条经过光电门所用的时间（挡光时间）。滑块$P$与竖直转轴间的距离可调。回答以下问题：

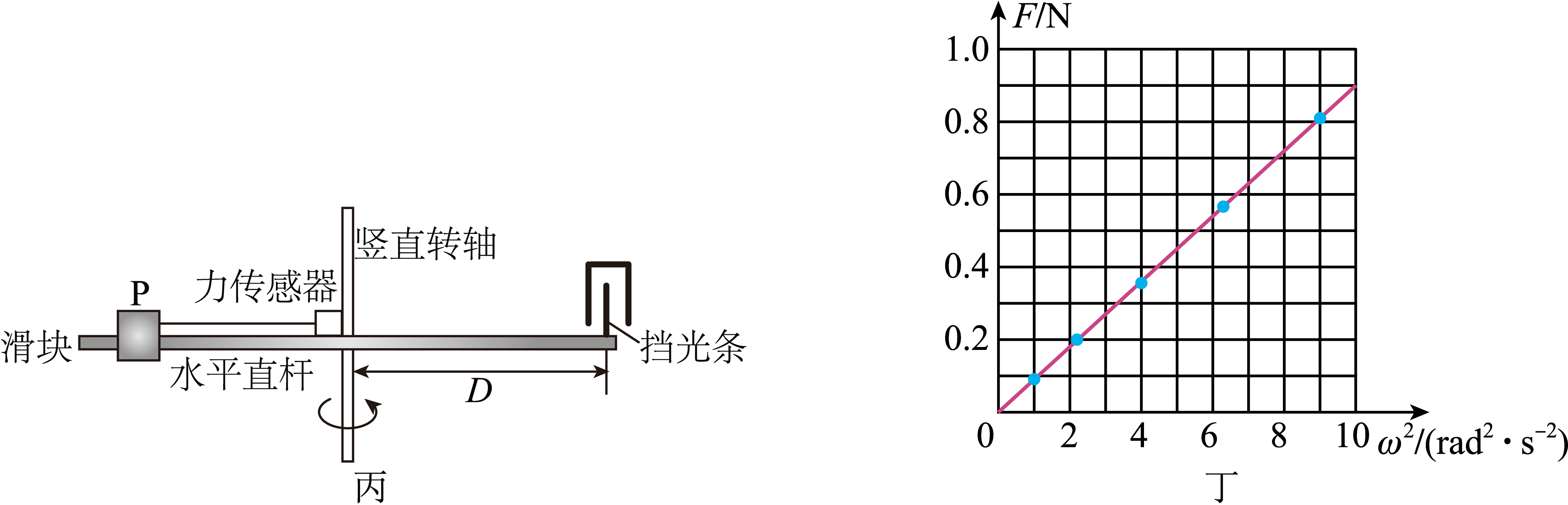
③若某次实验中测得挡光条的挡光时间伪$\Delta t$，则滑块$P$的角速度表达式为$\omega=$                ；

④实验小组保持滑块$P$质量和运动半径$r$不变，探究向心力$F$与角速度$\omega$的关系，作出$F-\omega^{2}$图线如图丁所示，若滑块$P$运动半径$r=0.2\ \rm m$，细线的质量和滑块与杆的摩擦可忽略，由$F-\omega^{2}$图线可滑块$P$质量$m=$                $\;\rm kg$（结果保留$2$位有效数字）。

$\\dfrac{d}{D\\Delta t}$；$0.44$

挡光条的线速度为$v=\dfrac{d}{\Delta t}$

则滑块$P$的角速度为$\omega=\dfrac{v}{r}=\dfrac{d}{D\Delta t}$

根据向心力大小公式$F=mr\omega^{2}$

所以$F-\omega^{2}$图线的斜率为$k=mr=\dfrac{\text{0.8\ N}}{\text{9\ rad}^{\text{2}} \cdot \text{s}^{-2}}$

解得，滑块$P$质量为$m\approx 0.44\;\rm kg$