| 带电粒子在等效重力场中的运动 题目答案及解析
稿件来源:高途
| 带电粒子在等效重力场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在等效重力场中的运动
如图所示,$BCD$是光滑绝缘的半圆形轨道,位于竖直平面内,直径$BD$竖直,轨道半径为$R$,下端与水平光滑绝缘轨道在$B$点平滑连接,整个轨道处在水平向左的匀强电场中。现有一质量为$m$、带正电的小球(可视为质点)由水平轨道上的$A$点静止释放,已知$AB$之间的距离$s=8R$,滑块受到的静电力大小为$0.5mg$,重力加速度为$g$。
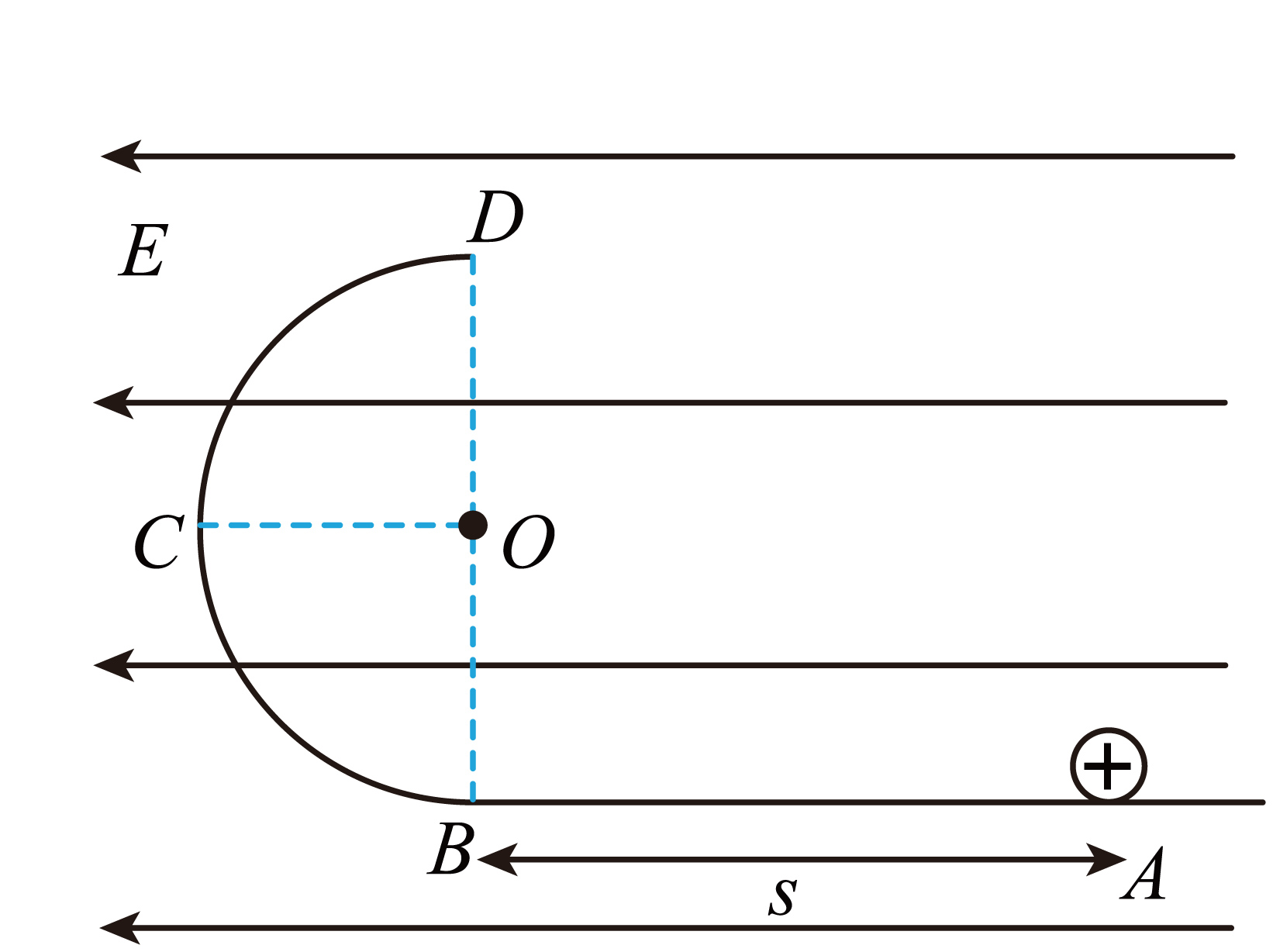
求小球到达$B$点时的速度大小;
$v_{B}=2\\sqrt{2gR}$
"]]小球从$A$到$B$做匀加速直线运动,由动能定理可得$F_{电}s=\dfrac{1}{2}mv_{B}^{2}-0$
解得$v_{B}=2\sqrt{2gR}$
小球到达$D$点时轨道对小球的弹力大小:
$F_{N}=3mg$
"]]小球从$A$到$D$的过程中,由动能定理可得$F_{电}s-2mgR=\dfrac{1}{2}mv_{D}^{2}-0$
小球在$D$点,由牛顿第二定律可得$F_{{N}}+mg=m\dfrac{v_{D}^{2}}{R}$
联立解得$F_{N}=3mg$
小球从$D$点飞出轨道后,落在水平地面上的Р点(未画出),求$PB$之间的距离。
$x=3R$
"]]小球从$D$点飞出轨道后做匀变速曲线运动,竖直方向有$2R=\dfrac{1}{2}gt^{2}$
水平方向有$a=\dfrac{F_{电}}{m}$
设$PB$之间的距离为$x$,则有$x=v_{D}t-\dfrac{1}{2}at^{2}$
联立解得$x=3R$
| 带电粒子在等效重力场中的运动题目答案及解析(完整版)
