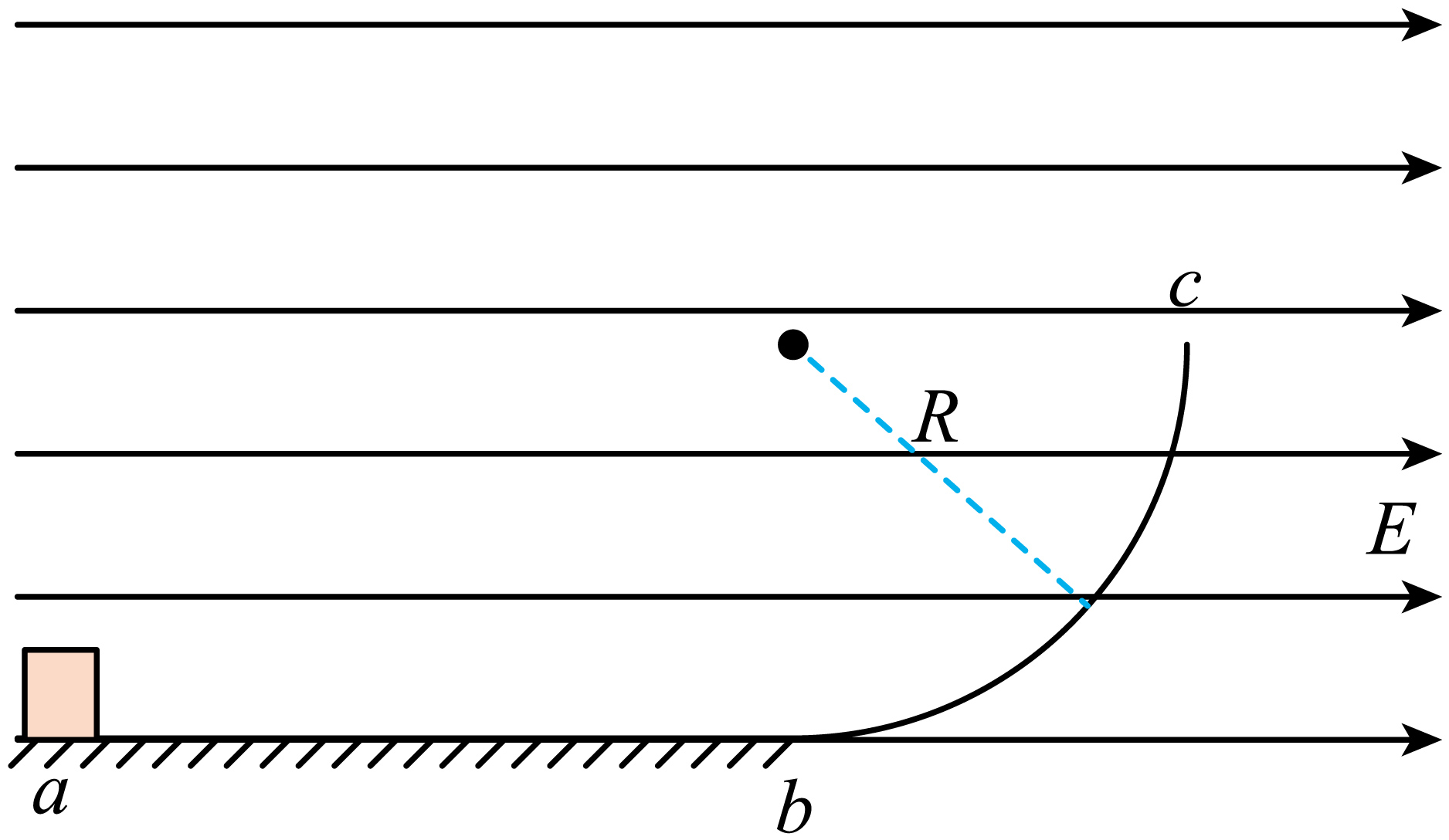
$ac$两点间的电势差大小

$\\dfrac{8mgR}{q}$

由公式$U=Ed$

得$ac$两点间的电势差大小$U_{ac}=E(3R+R)=\dfrac{8mgR}{q}$

物块运动到$c$点时对轨道的弹力大小；

$16mg$

物块从$a$到$c$，由动能定理有$U_{ac}q-mgR=\dfrac{1}{2}m{v_{c}}^{2}$

设在$c$点轨道对物块的支持力为$N$，有$N-Eq=m\dfrac{{v_{c}}^{2}}{R}$

得$N=16mg$

由牛顿第三定律有物块运动到$c$点时对轨道的弹力大小为$16mg$。

物块到达与$c$点等高的$d$点（图中未画出）时，距$c$点的水平距离；及求出$c$到$d$过程中的速度最小值。

$56R$，$2\\sqrt{\\dfrac{14gR}{5}}$

由（$2$）可知，在$c$点速度$v_{c}=\sqrt{14gR}$

在$c$之后，物块做类平抛运动，在竖直方向有$mg=ma_{y}$

上升到最高点时有$0=v_{c}-a_{y}t_{1}$

解得$t_{1}=\sqrt{\dfrac{14R}{g}}$

根据运动的对称性，则到达$d$点的总时间有$t=2t_{1}=2\sqrt{\dfrac{14R}{g}}$

在水平方向上有$qE=ma_{x}$，$x=\dfrac{1}{2}a_{x}t^{2}$

解得$x=56R$

物块离开$c$点后受到的合力为$F=\sqrt{(Eq)^{2}+(mg)^{2}}=\sqrt{5}mg$

设合力与水平方向夹角为$\theta$，有$\tan\theta=\dfrac{mg}{Eq}=\dfrac{1}{2}$

所以$\sin\theta=\dfrac{1}{\sqrt{5}}$

$c$到$d$过程中当速度方向与合力方向垂直时，速度有最小值，则最小速度等于$v_{C}$沿垂直合力方向的分量，大小为$v_{\min}=v_{C}\cos\theta=2\sqrt{\dfrac{14gR}{5}}$