高中 | 电表的改装 题目答案及解析
稿件来源:高途
高中 | 电表的改装题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.4 串联电路和并联电路
电表的改装
在实验室里,某实验小组设计了如图甲所示的电路图来测量未知电源的电动势和内阻,已知该未知电源的电动势约为$9\;\rm V$,内阻较大,该实验小组找来一个定值电阻$R_{0}=3\;\rm k\Omega$、一个滑动变阻器(最大值为$9999\;\rm \Omega$)、两个量程为$3\;\rm V$(内阻均已知,$R_{V}=3\;\rm k\Omega$)的电压表、一个开关、导线若干。
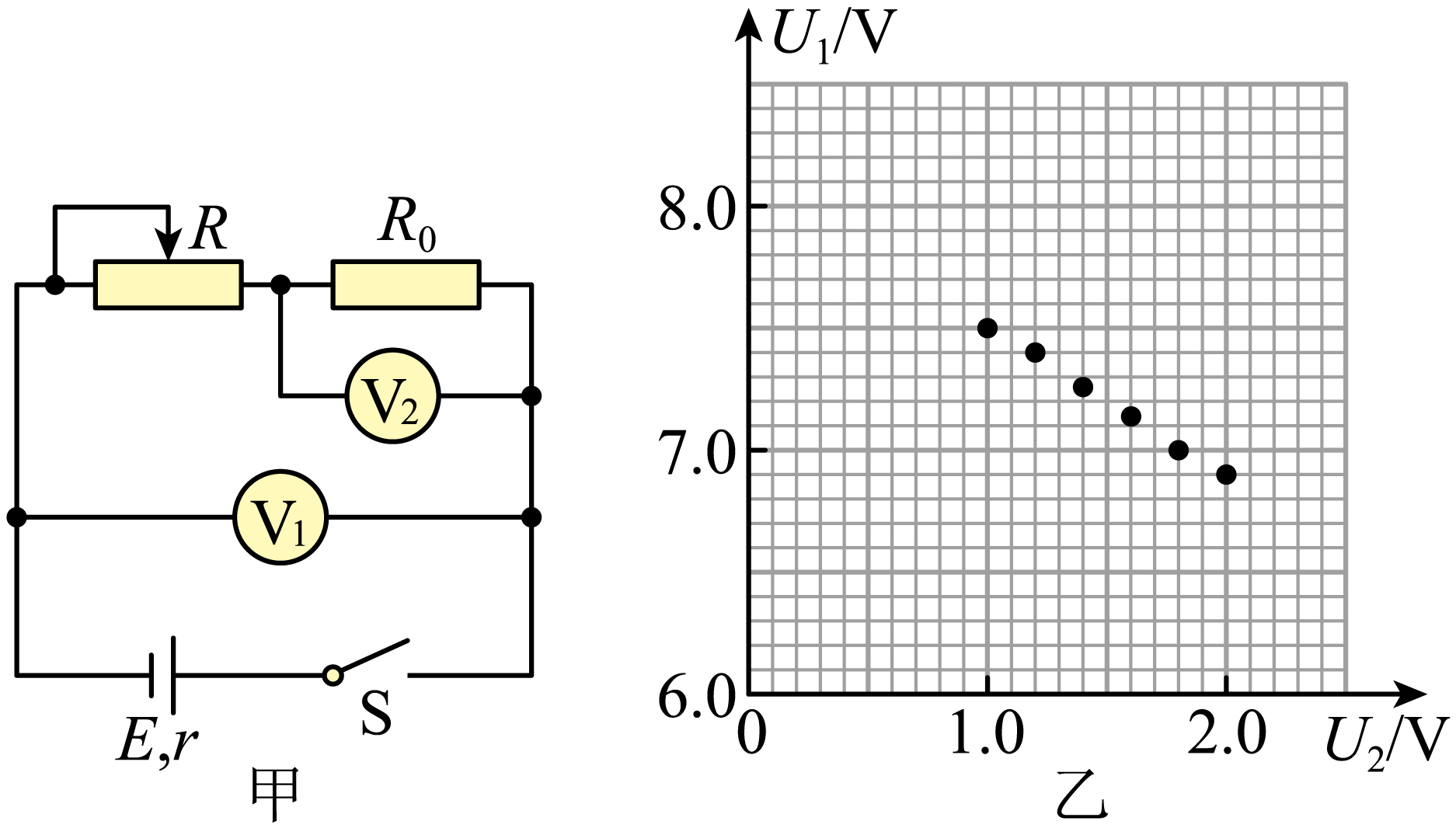
该实验小组想要一个量程为$9\;\rm V$的电压表$\rm V_{1}$,但是实验室没有$9\;\rm V$量程的电压表,于是利用量程为$3\;\rm V$的电压表改装成$9\;\rm V$的电压表,则需要将一个 $\;\rm \Omega$的电阻与量程为$3\;\rm V$的电压表串联,完成改装。
根据串联分压原理可知,量程为$3\;\rm V$的电压表需要串联的电阻分压$6\;\rm V$,则其电阻是$3\;\rm k\Omega$的两倍,即$6\;\rm k\Omega$。
图甲中,$\rm V_{1}$是改装后的电压表,实验小组按照图甲的电路图进行实验,测得多组实验数据记录在下表中,并在图乙中已经描出了前$6$个点,请完成第$7$个描点,并作出$U_{1}-U_{2}$的关系图线 。
| 电压表$\rm V_{1}$示数$\dfrac{U_{1}}{\text{V}}$ | $7.50$ | $7.39$ | $7.26$ | $7.13$ | $7.00$ | $6.88$ | $6.60$ |
| 电压表$\rm V_{2}$示数$\dfrac{U_{2}}{\text{V}}$ | $1.00$ | $1.20$ | $1.40$ | $1.60$ | $1.80$ | $2.00$ | $2.50$ |
见解析
"]]描点、作图如下
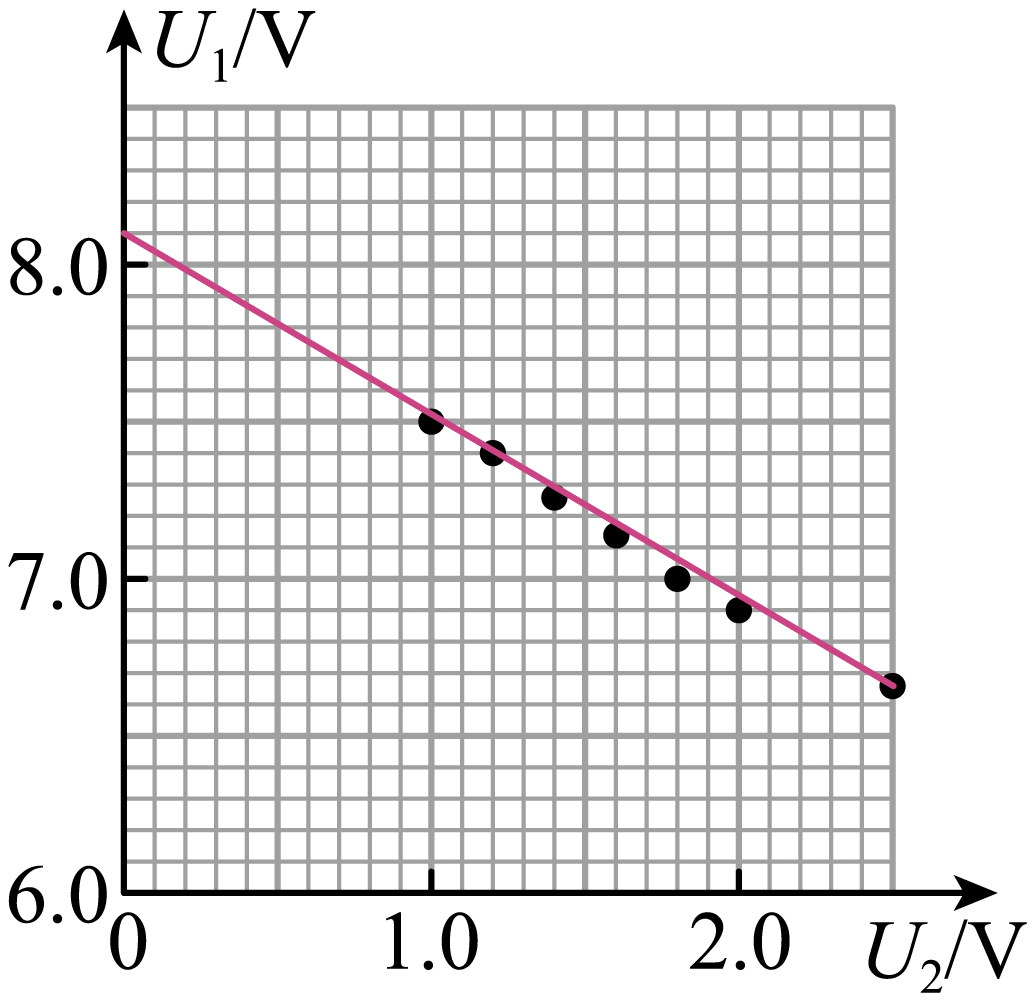
实验小组完成连线后,如果图线与纵轴的交点坐标为$(0,8.1\;\rm V)$,图线的斜率的绝对值为$0.6$,则通过计算可得电源的电动势为$E=$ $\;\rm V$,电源内阻$r=$ $\;\rm \Omega$。(结果均保留一位小数)
改装后的电压表内阻为$R_{V1}=9\;\rm k\Omega$,又电压表$\rm V_{2}$的内阻与$R_{0}$的电阻相等,
由闭合电路的欧姆定律,得$E=U_{1}+\left( \dfrac{U_{1}}{R_{{V1}}}+2\dfrac{U_{2}}{R_{0}} \right)r$
整理得$U_{1}=\dfrac{ER_{{V1}}}{r+R_{{V1}}}-\dfrac{2rR_{{V1}}}{R_{0}\left( r+R_{{V1}} \right)}U_{2}$
结合图像可看出,纵轴截距为$\dfrac{ER_{{V1}}}{r+R_{{V1}}}=8.1\;\rm \text{V}$
图线的斜率的绝对值为$\dfrac{2rR_{{V1}}}{R_{0}\left( r+R_{{V1}} \right)}=0.6$
联立以上两式并代入数据,解得$r=1000.0\;\rm \Omega$,$E=9.0\;\rm V$
高中 | 电表的改装题目答案及解析(完整版)
