用螺旋测微器测量合金丝的直径，如图所示，则合金丝的直径$d=$                  $\rm mm$；

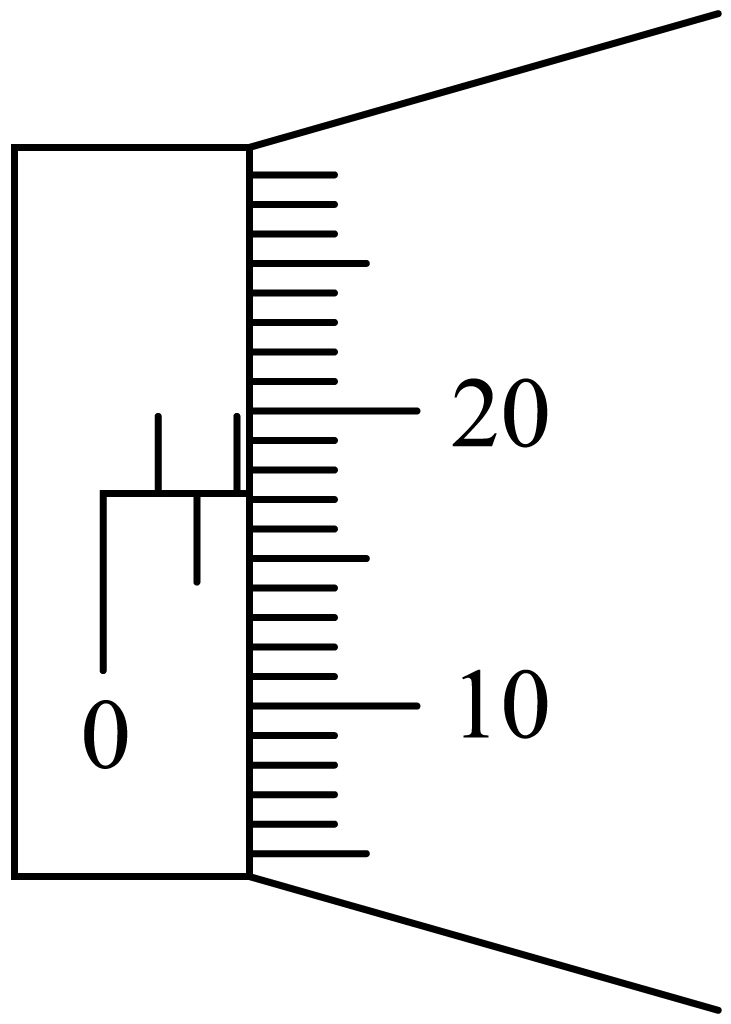
螺旋测微器精度为$\rm 0.01\ mm$，结合题中图像，可得直径$d=1.5\ \text{mm}+0.01\ \text{mm}\times17.1=1.671\ \text{mm}$。

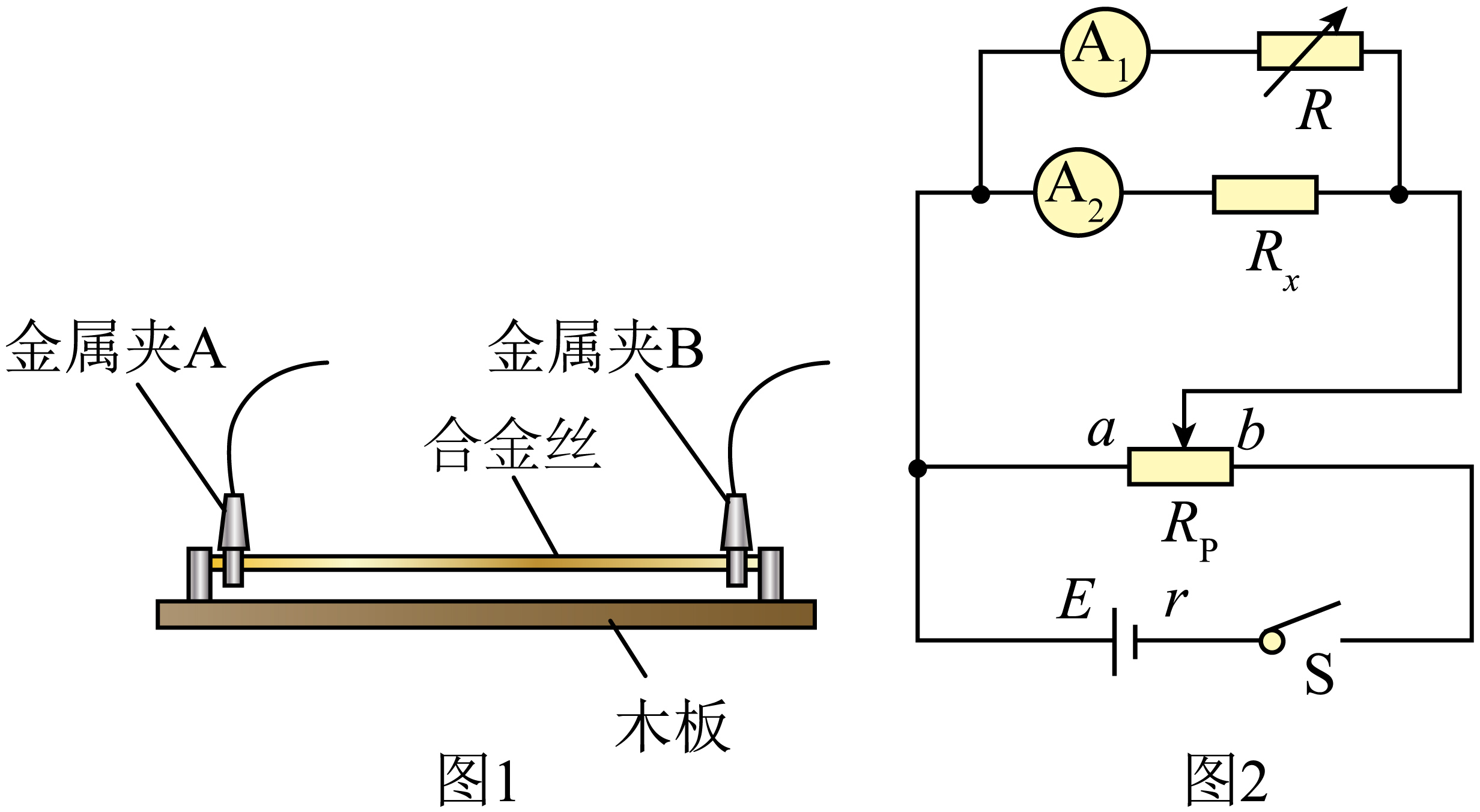
如图$1$所示，将合金丝${{R}_{x}}$固定在木板的两端，用带有金属夹$\rm A$、$\rm B$的导线将合金丝接入如图$2$所示电路，实验器材如下：

$\rm A$．电源$E$（电动势$\rm 8\ V$，内阻约为$0.5\ \Omega$）；

$\rm B$．电流表${{\text{A}}_{1}}$（$0\sim10\ \text{mA}$，内阻$R_{\text{A}}=3\ \Omega$）；

$\rm C$．电流表${{\text{A}}_{2}}$（$0\sim300\ \text{mA}$，内阻很小）；

$\rm D$．电阻箱（最大阻值$9999.9\ \Omega$）；

$\rm E$．滑动变阻器${{R}_{\text{p}}}$（阻值$0\sim10\ \Omega$）；

$\rm F$．开关$S$和导线若干。

现将电阻箱$R$与电流表${{\text{A}}_{1}}$改装为量程为$6V$的电压表，电阻箱的阻值应调为${{R}_{\text{0}}}=$                  $\Omega $；

电流表${{\text{A}}_{1}}$改装为量程为$6V$的电压表需要串联一个电阻，根据改装原理有

$U={{I}_{\text{g}}}\left( {{R}_{\text{A}}}+{{R}_{0}} \right)$

整理得

$R_{\text{A}}+R_{0}=\dfrac{U}{I_{\text{g}}}=\dfrac{6}{10\times10^{-3}}\ \Omega$

解得

$R_{0}=597.0\ \Omega$

移动金属夹$\rm B$至适当位置，用刻度尺测量两金属夹之间合金丝的长度$L$，将滑动变阻器的滑片调至$a$端，闭合开关$\rm S$，移动滑动变阻器的滑片，使电流表${{\text{A}}_{2}}$的示数达到最大值${{I}_{\text{g}}}$，记录电流表${{\text{A}}_{1}}$的示数$I$；

重复以上步骤，获得多组$I$、$L$数据，作出$I-L$图像如图所示。则$I-L$图像的斜率$k=$                  $\rm mA/cm$（保留两位有效数字），合金丝的电阻率$\rho =$                  （用${{R}_{0}}$、${{R}_{\text{A}}}$、$k$、$d$、${{I}_{\text{g}}}$表示）；

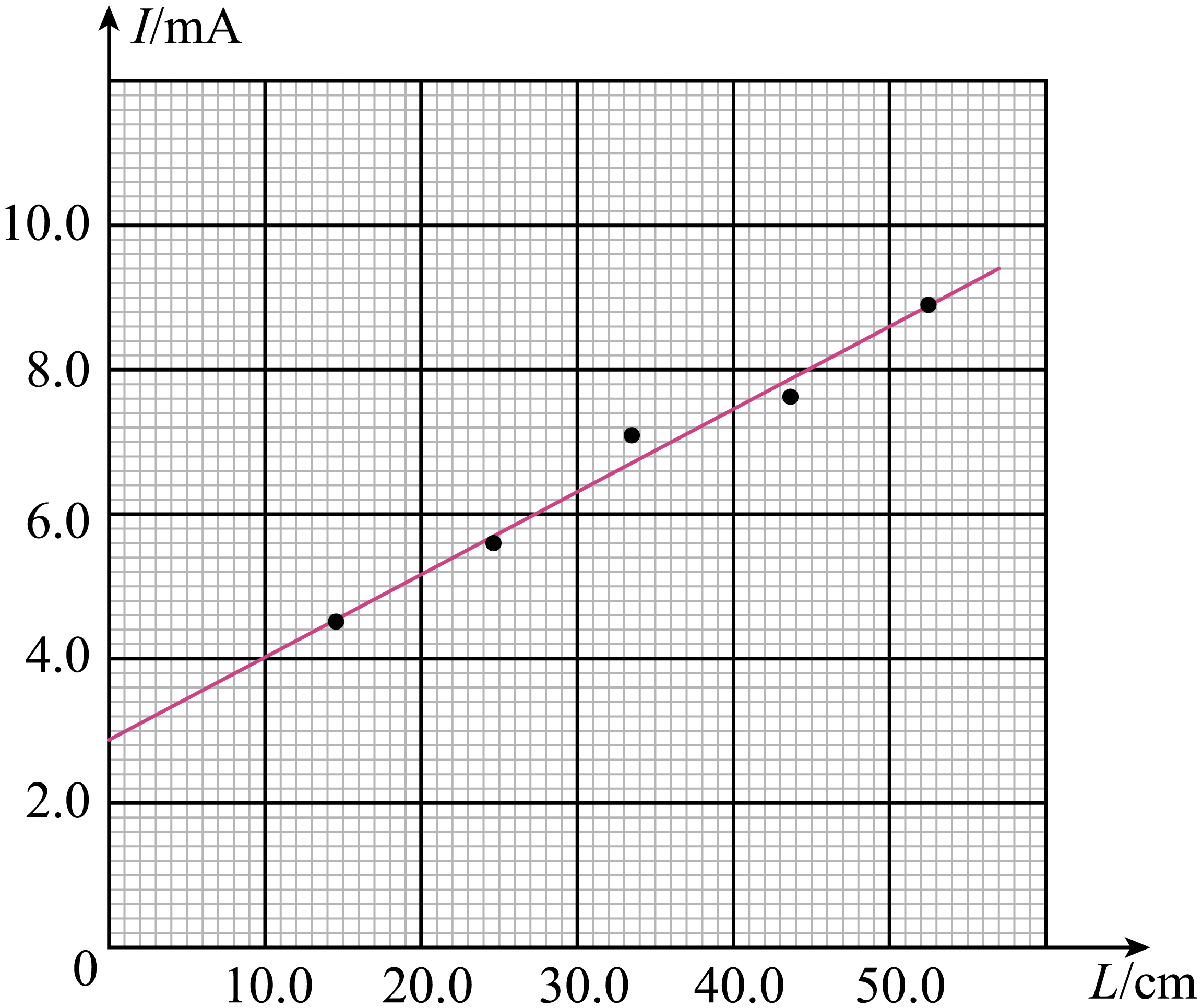
根据$I-L$图像可知斜率为$k=\dfrac{\text{ }\Delta\text{ }I}{\text{ }\Delta\text{ }L}=\dfrac{9.0-3.0}{55.0}\ \text{mA/cm}\approx\text{0}.11\ \text{mA/cm}$，由于电流表${{\text{A}}_{2}}$内阻很小，可忽略其内阻，结合图$2$，根据串联、并联关系有${{I}_{\text{g}}}{{R}_{x}}=I\left( {{R}_{\text{A}}}+{{R}_{0}} \right)$，又因为${{R}_{x}}=\rho \dfrac{L}{S}=\rho \dfrac{L}{\pi \dfrac{{{d}^{2}}}{4}}$，整理得$\dfrac{4\rho {{I}_{\text{g}}}}{\pi {{d}^{{{2}^{{}}}}}\left( {{R}_{\text{A}}}+{{R}_{0}} \right)}L=I$，可知$I-L$图像斜率$k=\dfrac{4\rho {{I}_{\text{g}}}}{\pi {{d}^{{{2}^{{}}}}}\left( {{R}_{\text{A}}}+{{R}_{0}} \right)}$，故电阻率为$\rho =\dfrac{k\pi {{d}^{2}}\left( {{R}_{0}}+{{R}_{\text{A}}} \right)}{4{{I}_{g}}}$

本实验中，若电流表${{\text{A}}_{2}}$的内阻不能忽略，则电阻率的测量值                  真实值（选填“大于”“小于”或“等于”）。

若电流表${{\text{A}}_{2}}$的内阻不能忽略，设其内阻为${{R}_{\text{A2}}}$，结合图$2$，根据串联、并联关系有${{I}_{\text{g}}}\left( {{R}_{x}}+{{R}_{\text{A2}}} \right)=I\left( {{R}_{\text{A}}}+{{R}_{0}} \right)$，又因为${{R}_{x}}=\rho \dfrac{L}{S}=\rho \dfrac{L}{\pi \dfrac{{{d}^{2}}}{4}}$，整理得$\dfrac{4\rho {{I}_{\text{g}}}}{\pi {{d}^{{{2}^{{}}}}}\left( {{R}_{\text{A}}}+{{R}_{0}} \right)}L+\dfrac{{{I}_{\text{g}}}}{\left( {{R}_{\text{A}}}+{{R}_{0}} \right)}{{R}_{\text{A2}}}=I$，可知$I-L$图像斜率与之前的斜率相同，故电阻率的测量值等于真实值。