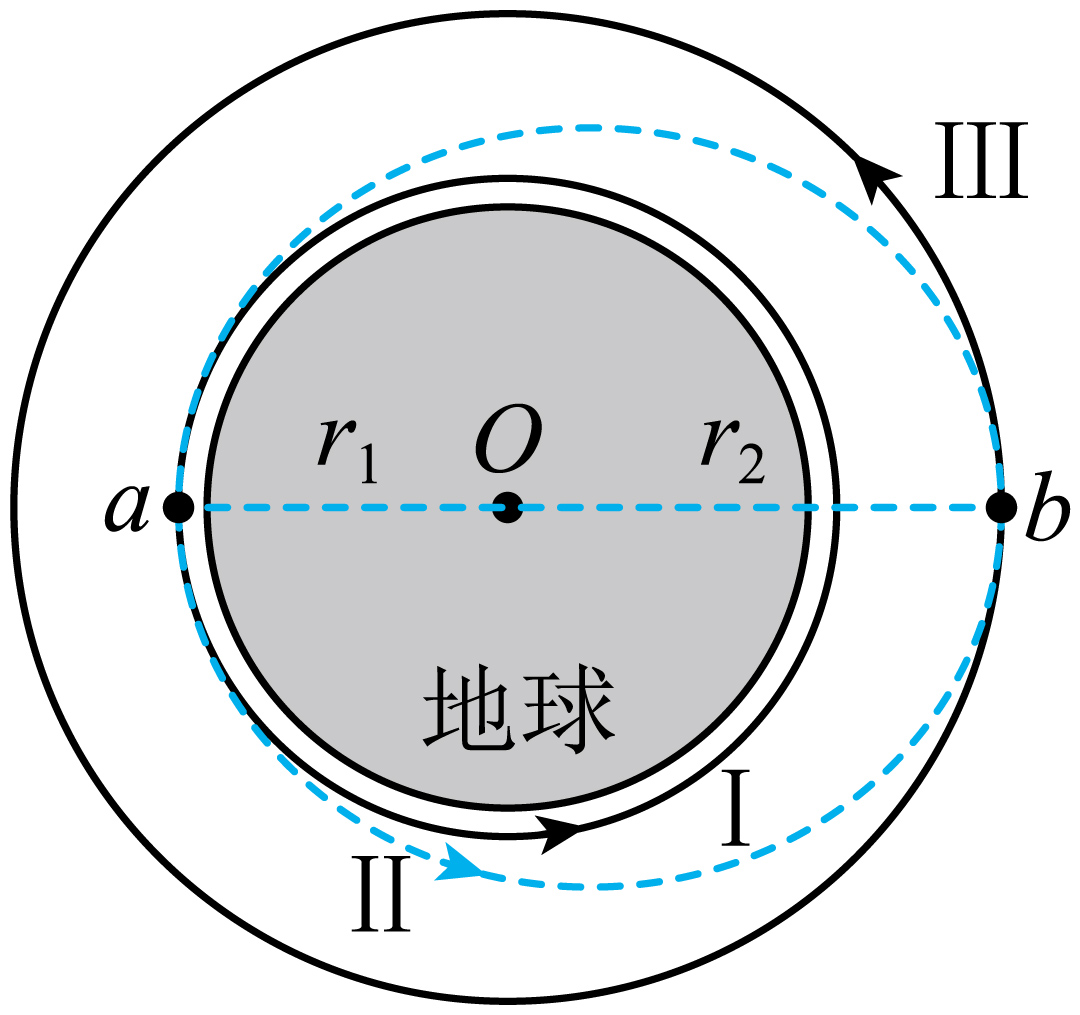
（多选）飞船的运行情况是$(\qquad)$

在$a$点由轨道$\\rm I$进入轨道$\\rm II$时要加速

在$b$点由轨道$\\rm II$进入轨道$\\rm III$时要减速

在轨道$\\rm I$上的运行速率大于在轨道$\\rm III$上的运行速率

在轨道$\\rm I$上的运行速率小于在轨道$\\rm III$上的运行速率

$\rm AB$．根据变轨原理可知，在$a$点由轨道$\rm I$进入轨道$\rm II$时要加速，在$b$点由轨道$\rm II$进入轨道$\rm III$时要加速，故$\rm A$正确，$\rm B$错误；

$\rm CD$．根据万有引力提供向心力有$\dfrac{GMm}{r^{2}}=m\dfrac{v^{2}}{r}$

解得$v=\sqrt{\dfrac{GM}{r}}$

可知，在轨道$\rm I$上的运行速率大于在轨道$\rm III$上的运行速率，故$\rm C$正确，$\rm D$错误；

故选：$\rm AC$。

已知万有引力常量为$G$，地球质量为$M$，天宫空间站总质量为$m$，则天宫空间站绕地球运行的周期为                 ，机械能为                 （以无穷远处为零势能面）。

根据万有引力提供向心力有$\dfrac{GMm}{r_{2}^{2}}= mr_{2}\dfrac{4\pi^{2}}{T^{2}}$

解得$T=2\pi\sqrt{\dfrac{r_{2}^{3}}{GM}}$

天宫空间站绕地球运行的势能为$E_{\text{p}}=- \dfrac{GMm}{r_{2}}$

根据万有引力提供向心力有$\dfrac{GMm}{r_{2}^{2}}=m\dfrac{v^{2}}{r_{2}}$

动能为$E_{\text{k}}=\dfrac{1}{2}mv^{2}=\dfrac{GMm}{2r_{2}}$

机械能为$E=E_{\text{k}}+E_{\text{p}}=- \dfrac{GMm}{2r_{2}}$

为保持与静置于地面上的钟快慢一致，需对天宫空间站里的钟进行校准。根据狭义相对论，空间站里的钟应调                 ；根据广义相对论，空间站里的钟应调                 （均选涂：$\rm A$．快    $\rm B$．慢）。最终需综合考虑两种相对论的效应进行校准。

空间站相对地球在高速运动，地球上的观察者看空间站的钟是慢的，应调快；

广义相对论是引力对时间的影响，引力势越低的地方，时间流逝越慢，空间站的引力势比地面高，则时间流逝更快，所以从广义相对论角度，应将时钟调慢。

在天宫空间站验证弹性碰撞。如图所示，将直径均为$D$的两个小球$a$、$b$静止放在同一直线$PQ$上，光电门垂直于$PQ$、放置在小球$b$的右侧。给小球$a$一个向右的初速度$v_{0}$，使小球$a$与$b$正碰。两小球碰撞后，先后经过光电门，依次记录下挡光时间$t_{1}$、$t_{2}$。

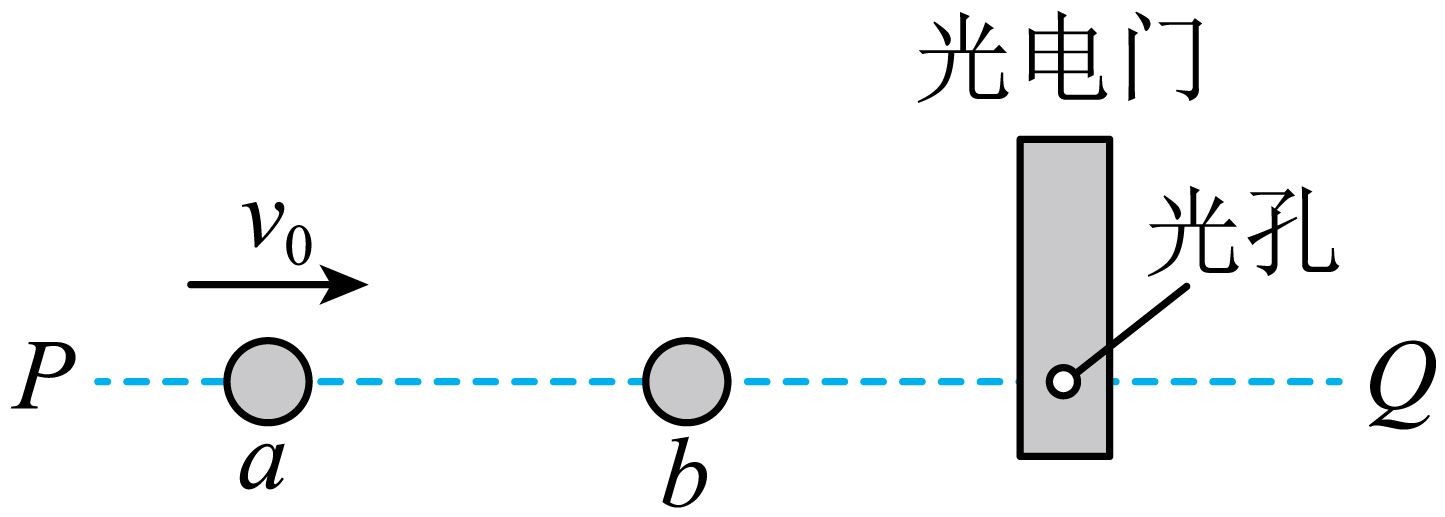
①小球$b$经过光电门的速度大小为                 。

②（计算）已知小球$a$、$b$的质量关系为$m_{a}=5m_{b}$，则当测得的$t_{1}$、$t_{2}$的比值$\dfrac{t_{1}}{t_{2}}$为多大时，即可验证小球$a$、$b$的碰撞为弹性碰撞                 ？

①小球$b$经过光电门的速度大小为$v_{b}=\dfrac{D}{t_{1}}$

②小球$a$经过光电门的速度$v_{a}=\dfrac{D}{t_{2}}$

两球发生弹性碰撞，碰撞过程系统动量守恒、机械能守恒，以向右为正方向，由动量守恒定律得$m_{a}v_{0}=m_{a}v_{a}+m_{b}v_{b}$

由机械能守恒定律得$\dfrac{1}{2}m_{a}{v_{0}}^{2}=\dfrac{1}{2}m_{a}{v_{a}}^{2}+\dfrac{1}{2}m_{b}{v_{b}}^{2}$

解得$v_{a}=\dfrac{2}{3}v_{0}$，$v_{b}=\dfrac{5}{3}v_{0}$

则$\dfrac{t_{1}}{t_{2}}=\dfrac{2}{5}$