在电场中$A$点，引入不同的试探电荷，会变化的是$(\qquad)$

$A$点的电场强度

$A$点的电势

在$A$点的电势能

$A$点与电场中另一点间的电势差

在电场中$A$点，引入不同的试探电荷，会变化的是不同的试探电荷在$A$点的电势能。试探电荷不会改变电场本身的性质，即不会改变$A$点的电场强度与电势，以及$A$点与电场中另一点间的电势差。

故选：$\rm C$。

如图所示是三个电场的等势面，$A$、$B$ 两点在等势面上。若带电量为$+1\;\rm \mu C$ 的物体从 $A$ 点移动到 $B$ 点，三种情况下电场力做功分别为 $W_{\rm Ⅰ}$、$W_{\rm Ⅱ}$、$W_{\rm Ⅲ}$，则$(\qquad)$

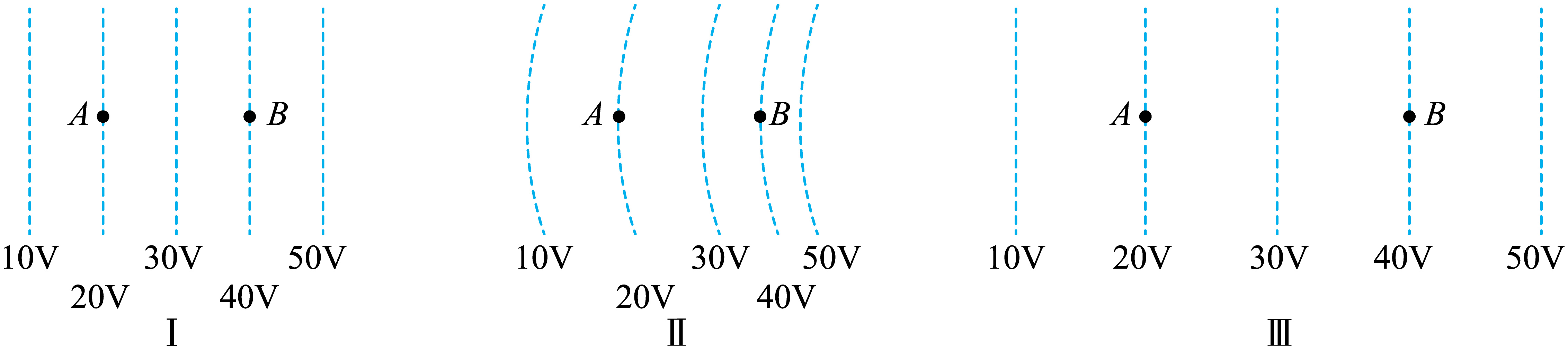
$W_{\\rm Ⅰ }$最大

$W_{\\rm Ⅱ }$最大

$W_{\\rm Ⅲ}$ 最大

$W_{\\rm Ⅰ}=W_{\\rm Ⅱ}\\lt W_{\\rm Ⅲ}$

$W_{\\rm Ⅰ }=W_{\\rm Ⅱ}=W_{\\rm Ⅲ}$

根据电场力做功$W_{AB}=qU_{AB}$，因三个电场中$A$点到$B$点的电势差均相等，故三种情况下电场力做功相同，即$W_{\rm Ⅰ}=W_{\rm Ⅱ}=W_{\rm Ⅲ}$

故选：$\rm E$。

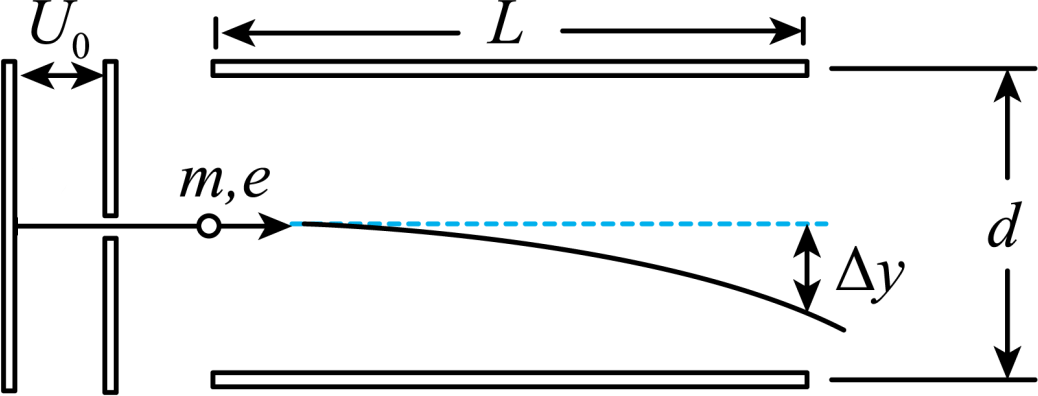
示波器可以利用电场对被加速的电子的偏转来观察电信号随时间变化的情况。示波器的基本原理如图所示，电子由静止开始经加速电场加速后，沿平行于板面的方向射入偏转电场，并从另一侧射出。已知电子质量为 $m$，电荷量为$-e$，加速电场电压为 $U_{0}$。偏转电场可看作匀强电场，由加在平行电极板上的待测信号电压产生，已知极板长度为 $L$、板间距为 $d$。忽略电子所受重力。

①（计算）求电子射入偏转电场时的初速度大小$v_{0}$；

②（计算）若已知电子从电场射出时沿垂直板面方向的偏转距离为 $\Delta y$，求待测信号电压 $U$ 的大小。

③对同一待测电信号，若要使偏转距离 $\Delta y$ 更大，请提出一种可行的办法

$\\sqrt{\\dfrac{2eU_{0}}{m}}$；

答：$\\dfrac{4U_{0}d\\Delta y}{L^{2}}$；

答：仅减小加速电场电压 $U_{0}$（或仅减小 $d$ 或仅增大 $L$）

①对电子在加速电场被加速的过程，根据动能定理得$eU_{0}=\dfrac{1}{2}m{v_{0}}^{2}$

解得$v_{0}=\sqrt{\dfrac{2eU_{0}}{m}}$

②电子在偏转电场中做类平抛运动，则由平行于极板方向做匀速直线运动得$L=v_{0}t$

由垂直于极板方向做匀加速直线运动得$\Delta y=\dfrac{1}{2}at^{2}$

根据牛顿第二定律得$\dfrac{eU}{d}=ma$

联立解得$U=\dfrac{4dU_{0}\Delta y}{L^{2}}$

③由$U=\dfrac{4dU_{0}\Delta y}{L^{2}}$，可得$\Delta y=\dfrac{UL^{2}}{4dU_{0}}$

对同一待测电信号，即$U$一定，要使偏转距离$\Delta y$更大，一种可行的办法是仅减小加速电压$U_{0}$（或仅减小$d$或仅增大$L$）。