（简答）列式说明雨滴在整个下落过程中作怎样的运动；

见解析

设雨滴质量为 $m$，加速度为 $a$，对雨滴受力分析如图所示

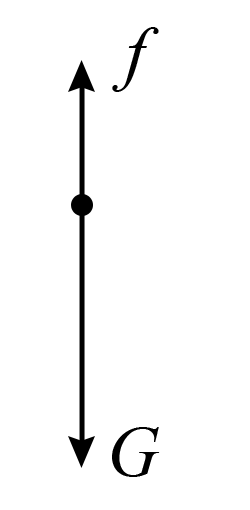
由牛顿第二定律得$mg-f=ma$

结合题意$f=kr^{2}v^{2}$，可得$a=g-\dfrac{kr^{2}v^{2}}{m}$

雨滴下落过程，$a$与$v$同向，故$v$增大；随着$v$增大，$f$增大，$a$减小，当$f=mg$时，$a$减小到零。则雨滴先做加速度减小的加速运动，至加速度为零，接着做匀速直线运动。

（简答）设雨滴的密度为$\rho$，推导雨滴下落过程中的最大速度$v_{m}$与半径$r$的关系式；

$v_{\\text{m}}= \\sqrt{\\dfrac{4\\pi\\rho gr}{3k}}$

当加速度减小为零时，雨滴趋近于最大速度$v_{m}$，则有$a=g-\dfrac{kr^{2}v_{\text{m}}^{2}}{m}=0$

雨滴质量为$m=\rho \cdot \dfrac{4}{3}\pi r^{3}$

联立解得$v_{\text{m}}=\sqrt{\dfrac{4\pi\rho gr}{3k}}$

设某雨滴刚开始下落时的机械能为$E_{0}$，离地高度为$H$。在图中定性画出雨滴从静止开始下落到落地的整个过程中，雨滴机械能$E$随雨滴下落高度$h$变化的$E-h$图像；

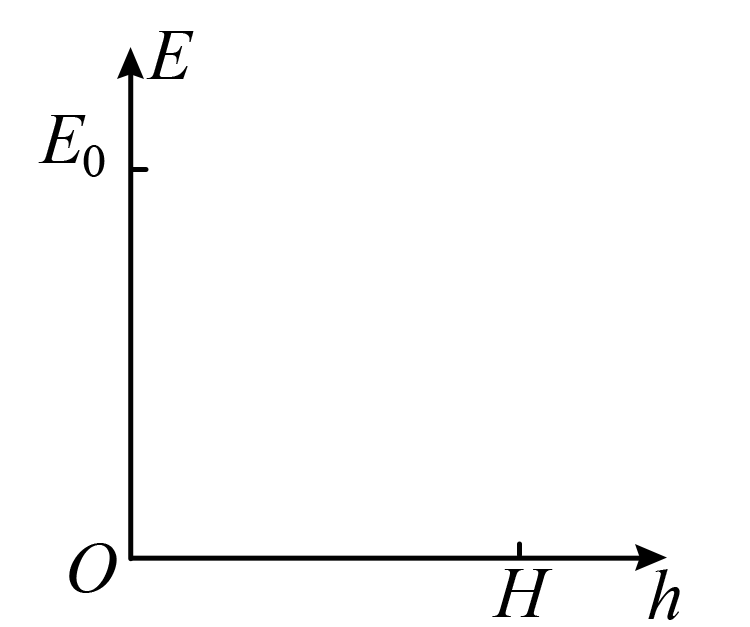
图像见解析；

设某雨滴刚开始下落时的机械能为$E_{0}$，离地高度为$H$，根据功能关系可知，克服空气阻力做的功等于雨滴机械能的减小量，则$E-h$图像的斜率绝对值表示空气阻力大小，由于空气阻力$f$增大，所以$E-h$图像的斜率绝对值逐渐增大，则$E-h$图像如图所示

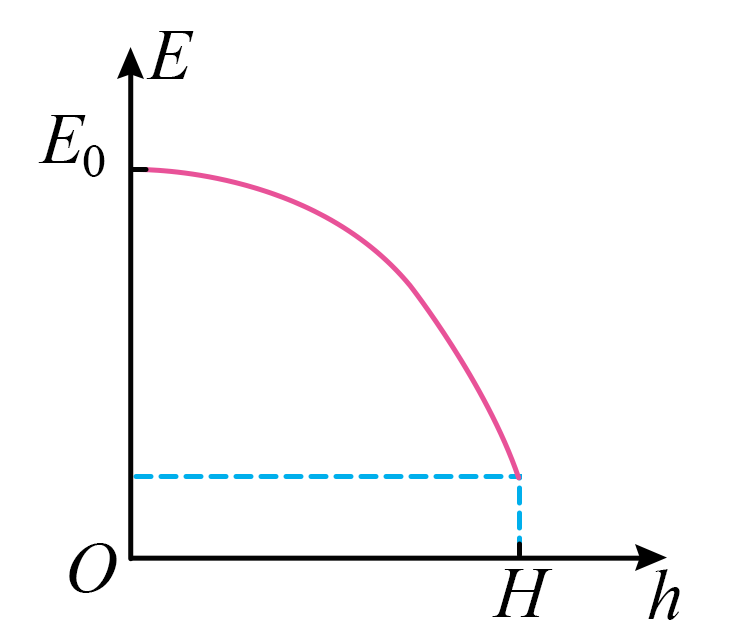
（论证）由于大量气体分子在各方向运动的几率相等，其对静止雨滴的作用力为零。将雨滴简化为垂直于运动方向面积为$S$的圆盘，设单位体积内空气分子数为$n$，空气分子质量为$m_{0}$，证明：圆盘以速度$v$下落时受到的空气阻$f∝v^{2}$。

见解析

根据题设条件：大量气体分子在各方向运动的几率相等，其对静止雨滴的作用力为零。以下只考虑雨滴下落的定向运动，简化的圆盘模型如图所示

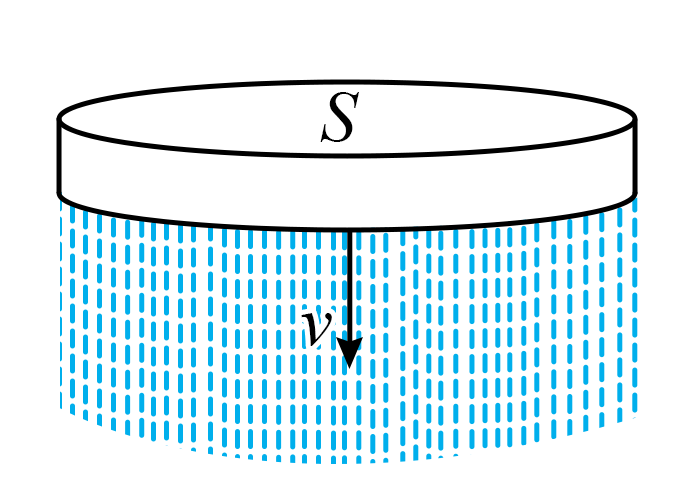
设空气分子与圆盘碰撞前后相对速度大小不变，在$\Delta t$时间内，与圆盘碰撞的空气分子质量为$\Delta m$，圆盘对气体分子的作用力为$F$，则有$\Delta m=Sv\Delta t ⋅ nm_{0}$

对$\Delta t$时间内被圆盘碰撞的空气分子，根据动量定理可得$F\Delta t∝\Delta mv$

联立可得$F∝nm_{0}Sv^{2}$

根据牛顿第三定律，可知圆盘所受空气阻力$f∝v^{2}$