在平静的湖面上，用一根树枝周期性地轻轻点动水面，形成一个振动的波源，水波向四周传开。把水波看成是简单的机械横波。发现水面上传播出去的波形如图所示，其中实线表示波峰，虚线表示波谷，$S$是波源位置。产生这一现象的可能原因$(\qquad)$

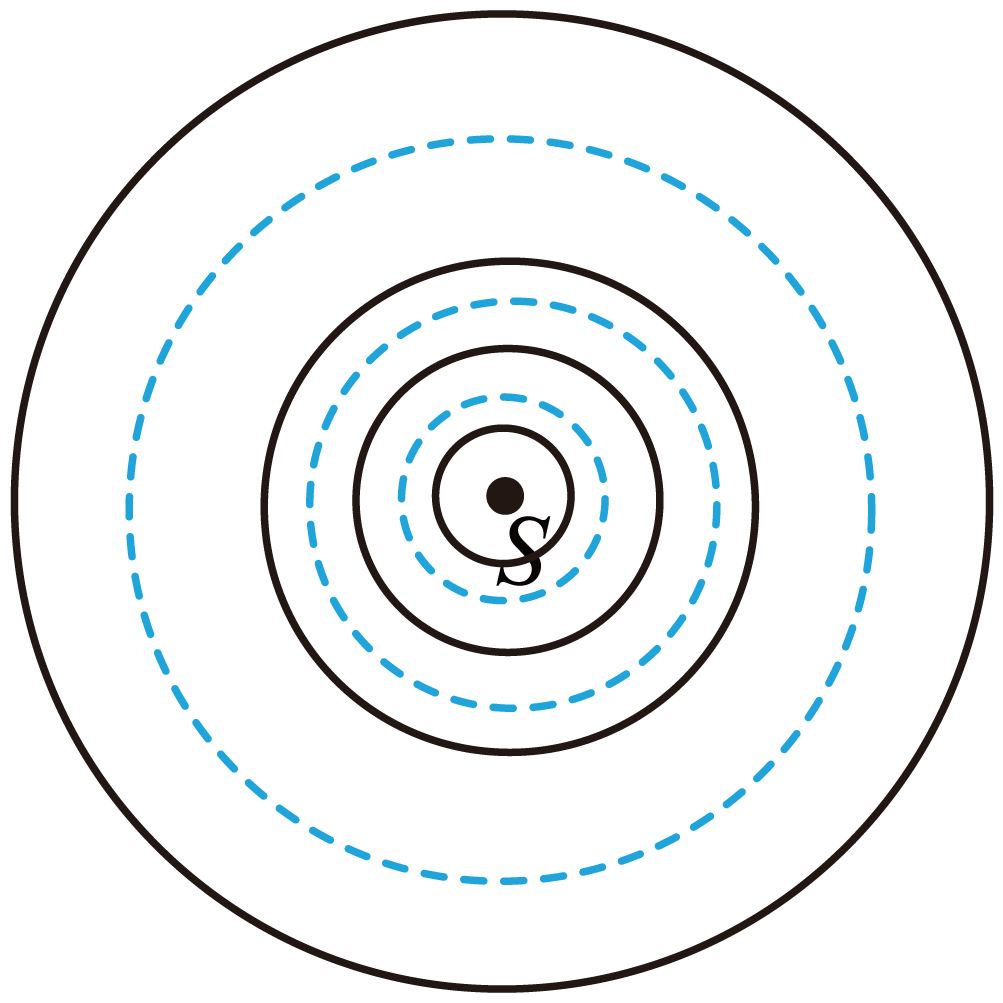
树枝振动强度逐渐增强

树枝振动强度逐渐减弱

树枝振动频率逐渐加大

树枝振动频率逐渐减小

$\rm AB$．机械波的强度与振幅有关，强度越大，振幅越大；强度越小，振幅越小。而题目中给出的波形图反映的是波的频率等特性相关变化情况，并没有体现出振幅的变化，波形图中波峰到平衡位置、波谷到平衡位置的距离并没有改变，也就是振幅没有改变。所以树枝振动强度逐渐增强或逐渐减弱都不符合波形图所展示的现象，故$\rm AB$错误；

$\rm CD$．频率决定了单位时间内波振动的次数，当树枝振动频率逐渐加大时，在相同的传播距离内，会有更多的波峰和波谷出现，也就是波长会变短；相反，当树枝振动频率逐渐减小，在相同的传播距离内，波峰和波谷的数量会减少，波长会变长。观察题目中给出的波形图可以发现，越远离波源，波峰和波谷的间距（即波长）在逐渐变长，这意味着越远离波源的区域，频率越小，而振源最近时间内的振动产生的波靠近振源，此区域内波峰和波谷的间距（即波长）较小，频率较大，故推知产生这一现象的可能原因是树枝振动频率逐渐加大，故$\rm C$正确，$\rm D$错误。

故选：$\rm C$。

把一列水波看作是简谐横波，图为某时刻的波形图。此时$P$点沿$y$轴正方向向上运动，经过$0.75\;\rm s$第一次返回平衡位置。则该波的传播方向为                 （填“向左”或“向右”），其波速$v=$                 $\;\rm m/s$。

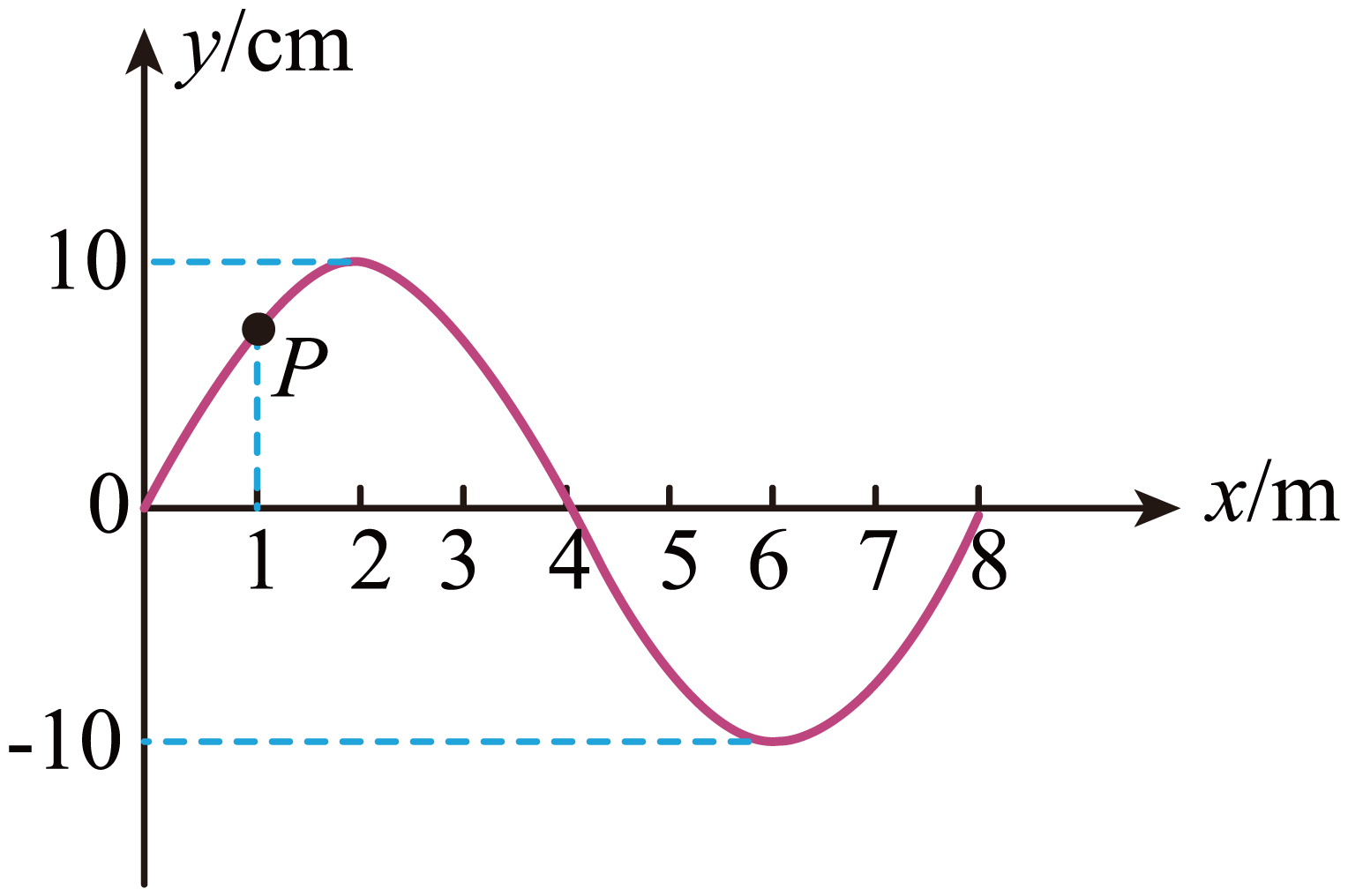
$P$点沿$y$轴正方向向上运动，根据同侧法知，波的传播方向为向左，又经过$0.75\;\rm s$第一次返回平衡位置，根据波形图知$\dfrac{\dfrac{3\pi}{4}}{2\pi} \times T= 0.75\;\rm \text{s}$

解得$T=2\;\rm s$

故波速$v=\dfrac{\lambda}{T}=\dfrac{8\ \text{m}}{2\ \text{s}}=4\;\rm \text{m/s}$

在平静湖面的底部有个固定的水下景观点光源，分别向各个方向交替发射红光和蓝光，已知水对两种光的折射率分别为$n_{红}$和$n_{蓝}$，且$n_{红}\lt n_{蓝}$。可以在湖面上看到一个圆形亮斑，则红光亮斑面积                 蓝光亮斑面积（填：“大于”、“等于”或“小于”），若光源离湖面的深度为$h$，则红光亮斑的面积大小为$S=$                 。

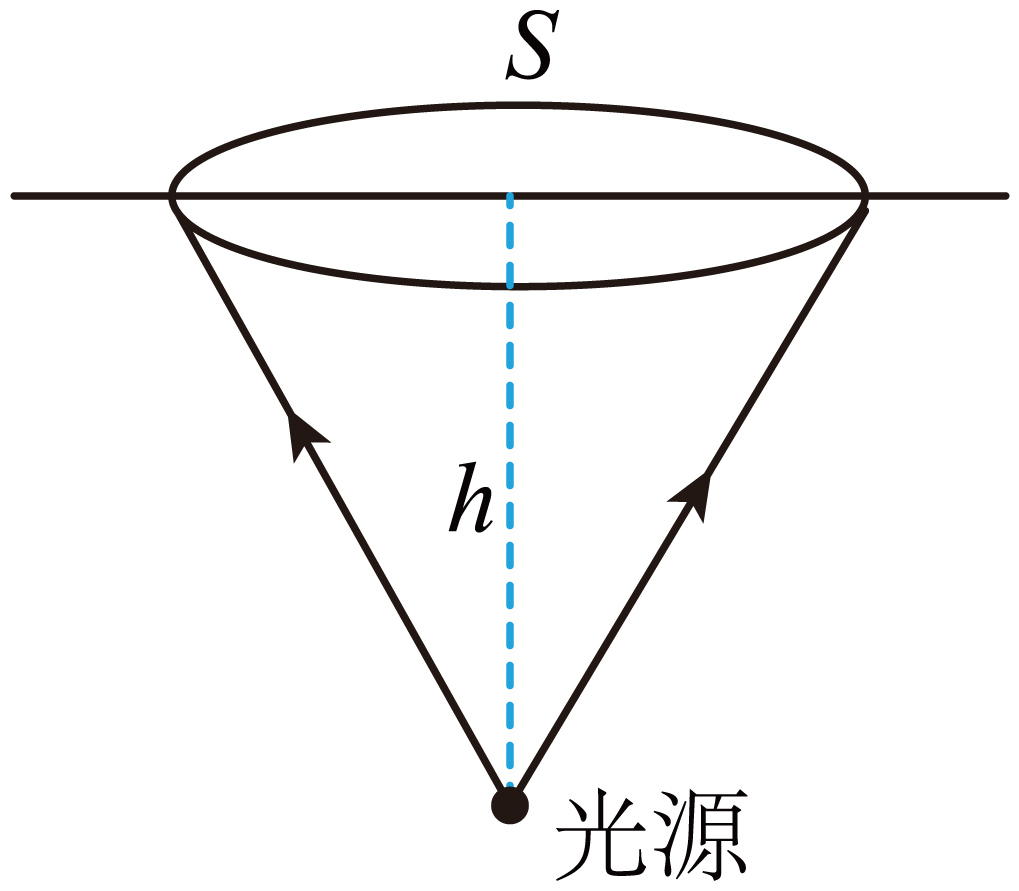
水下点光源发出的光射向湖面，当入射角大于临界角时会发生全反射，在湖面能看到的圆形亮斑是由于光能够折射出水面以及在临界角范围内的光形成的。根据$\sin C=\dfrac{1}{n}$

及$n_{红}\lt n_{蓝}$

知红光临界角大，所以在湖面上形成的圆形亮斑半径更大，根据圆的面积公式$S=\pi r^{2}$（$r$为圆半径）可知，红光亮斑面积大于蓝光亮斑面积。

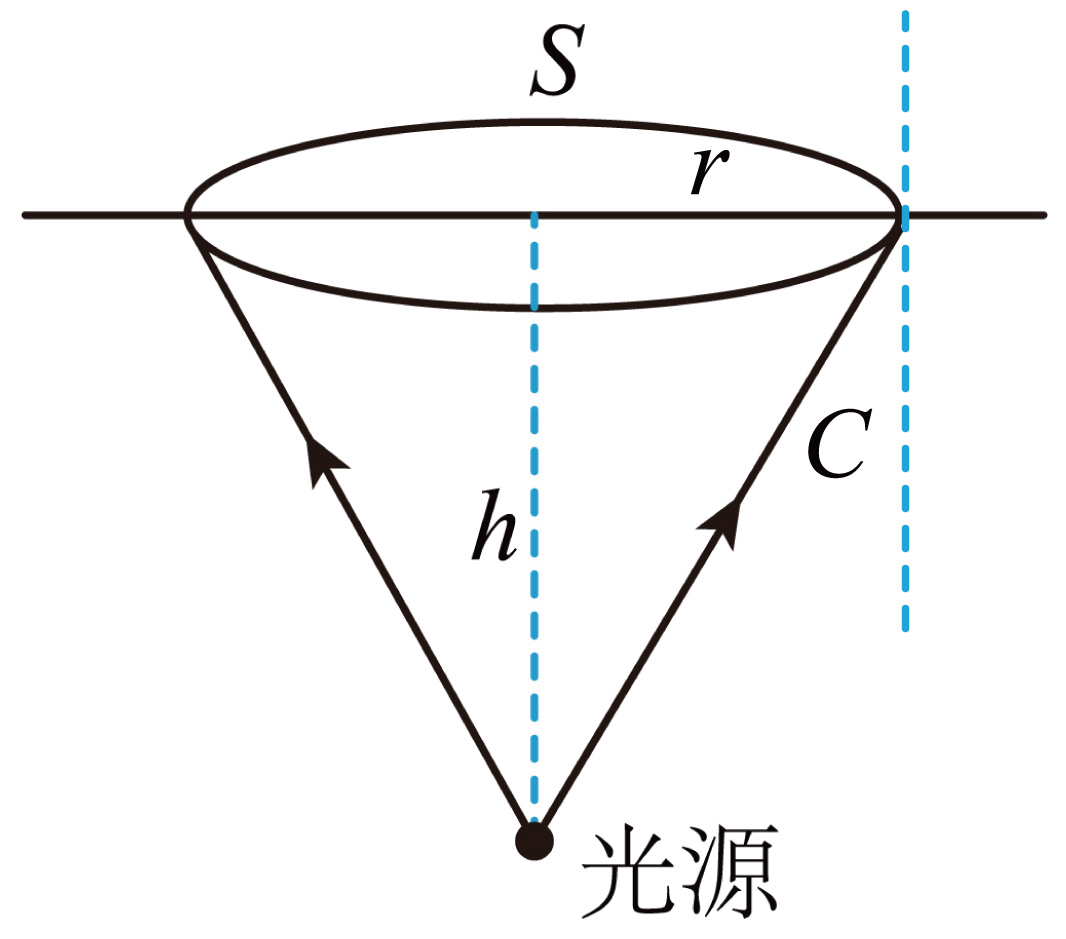
对于红光$\sin C=\dfrac{1}{n_{红}}=\dfrac{r}{\sqrt{r^{2}+h^{2}}}$

联立解得$r^{2}=\dfrac{h^{2}}{n_{红}^{2}-1}$

故亮斑的面积大小为$S=\pi r^{2}=\dfrac{\pi h^{2}}{n_{红}^{2}-1}$

在湖底腐烂的植物释放出沼气，形成一个气泡。假设气泡内气体质量保持不变，且可以看作理想气体。

①计算：若上升过程中泡内气体温度保持不变，气泡达到湖面时体积变为原来的$1.5$倍。湖面处大气压为$p_{0}=1.01 \times 10^{5}\;\rm pa$，水的密度$\rho=1.0 \times 10^{3}\;\rm kg/m^{3}$，重力加速度$g=9.8\;\rm m/s^{2}$。求湖水的深度是多少？                 （保留三位有效数字）

②若把气泡看作是一个封闭系统，在上升过程中，其对外做功$0.5\;\rm J$，同时内能增加$1.5\;\rm J$，则气体一定                 

$\rm A$．放出热量$2\;\rm J$      $\rm B$．吸收热量$2\;\rm J$      $\rm C$．放出热量$1\;\rm J$      $\rm D$．吸收热量$1\;\rm J$

上升过程中泡内气体温度保持不变，根据玻意耳定律$PV=P_{0}⋅1.5\;\rm V$

解得$P=1.5P_{0}$

又$P=1.5P_{0}=P_{0}+\rho gh$

联立解得$h=5.15\;\rm m$

根据题意有$W=-0.5\;\rm J$，$\Delta U=1.5\;\rm J$

根据热力学第一定律$\Delta U=W+Q$

解得$Q=2.0\;\rm J$

故则气体一定吸收热量$2\;\rm J$。

故选：$\rm B$。

如图所示，在一足够宽的河面上，一渡船从河岸边的$A$点出发，相对河水由静止开始做匀加速直线运动，加速度$a=0.5\;\rm m/s^{2}$，方向始终垂直河岸。已知河水的速度$v=5\;\rm m/s$不变。

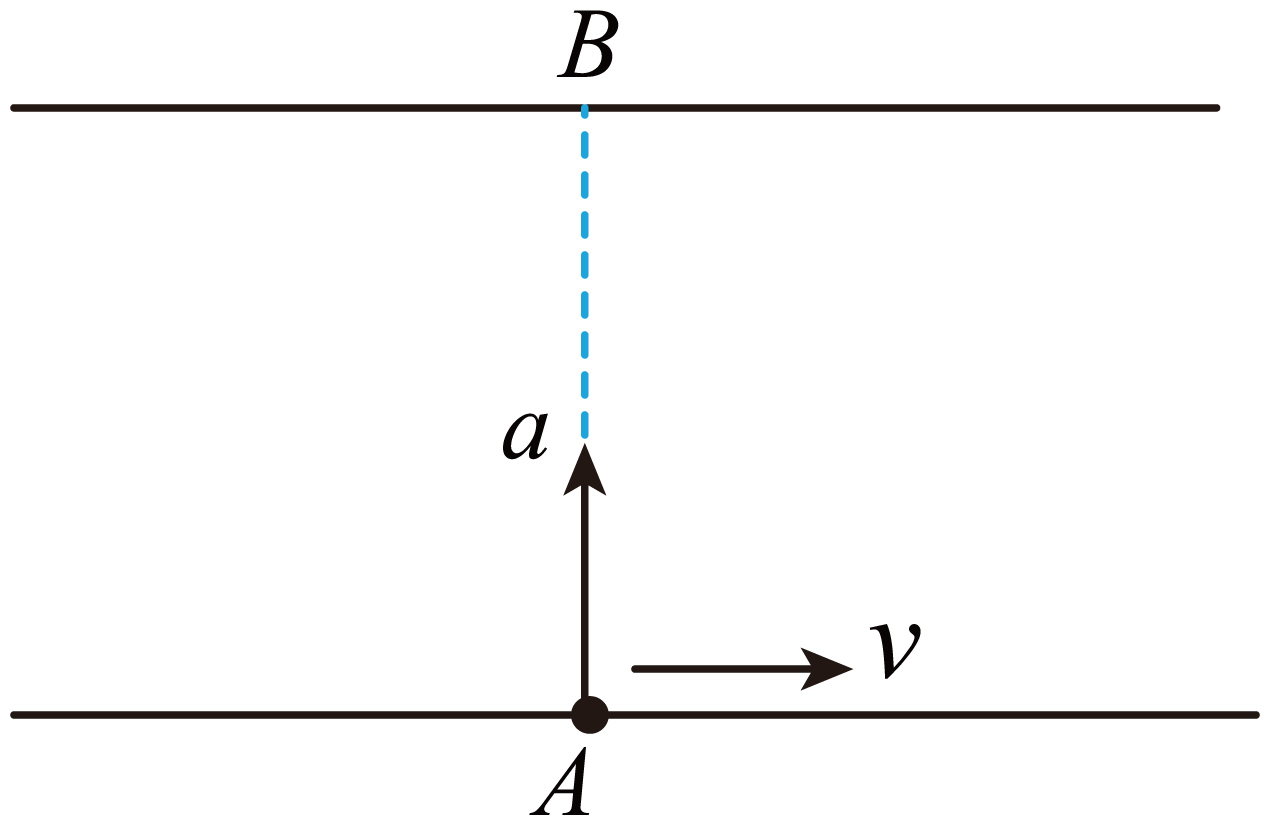
①船相对河岸的运动轨迹可能是       

$\rm A$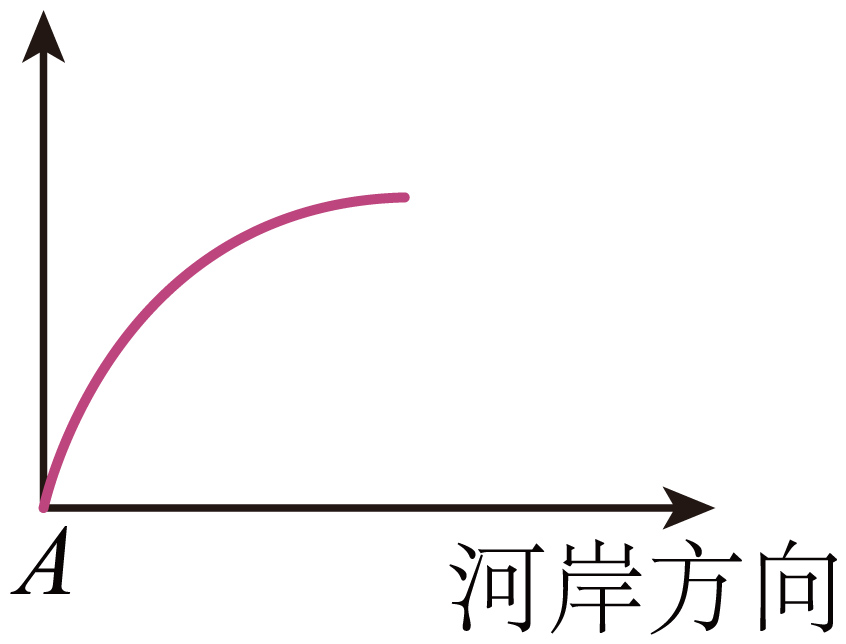．         $\rm B$．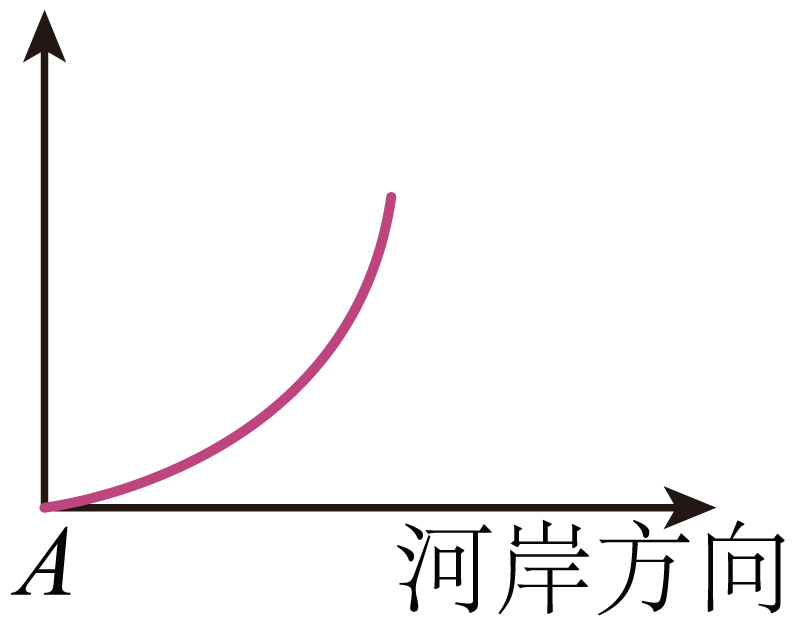

$\rm C$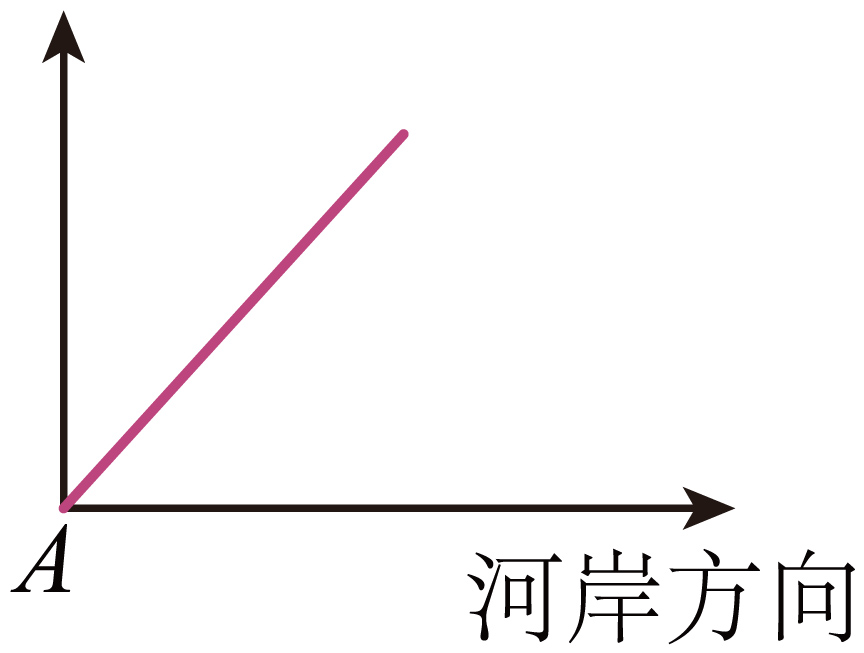．         $\rm D$．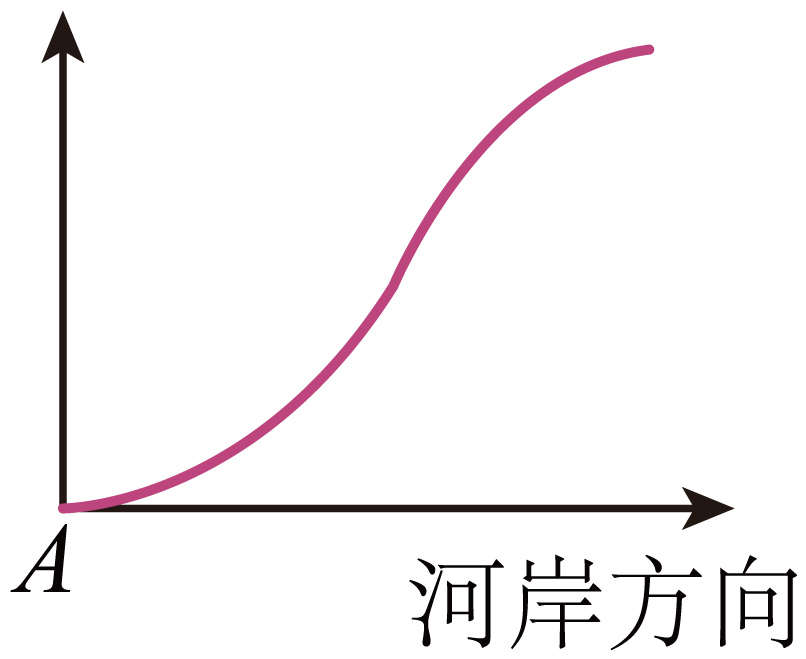

②船运动$20\;\rm s$时相对河岸的位移大小       。

根据合运动及分运单的关系，及曲线向力的方向弯曲知轨迹向垂直河岸方向弯曲。

故选：$\rm B$。

船运动$20\;\rm s$时相对河岸的位移大小$S=\sqrt{\left( \dfrac{1}{2}at^{2} \right)^{2}+(vt)^{2}}=100\sqrt{2}\;\rm \text{m}$

又$\tan\theta=\dfrac{\dfrac{1}{2}at^{2}}{vt}=1$

故方向与河岸的夹角为$45^\circ $。