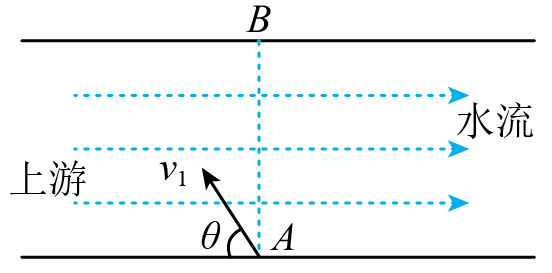
如图，小船以大小为v₁=5m/s、船头与上游河岸成θ=60°角的速度（在静水中的速度）从A处过河，经过一段时间正好到达正对岸B处。已知河宽d=180m，则下列说法中正确的$(\quad\ \ \ \ )$

河中水流速度为2.5$\\sqrt{3}$m/s

小船以最短位移渡河的时间为24$\\sqrt{3}$s

小船渡河的最短时间为24s

小船以最短时间渡河时到达对岸的位移是90$\\sqrt{5}$m

A．河中水流速度为

$v_{1}=v_{1}cos 60^{∘}=2.5m/s$

选项A错误；

B．小船以最短位移渡河的时间为

$t=\frac{d}{v_{1}\sin 60^{^\circ}}=\frac{180}{5 \times \frac{\sqrt{3}}{2}}\text{s}=24\sqrt{3}\text{s}$

选项B正确；

C．当船头方向指向正对岸时过河时间最短，则小船渡河的最短时间为

$t_{\min}=\frac{d}{v_{1}}=\frac{180}{5}\text{s=36s}$

选项C错误；

D．小船以最短时间渡河时到达对岸沿水流方向的位移是

$x=v_{2}t_{min}=2.5 × 36m=90m$

则总位移

$s=\sqrt{d^{2}+x^{2}}=90\sqrt{5}\text{m}$

选项D正确。

故选BD。