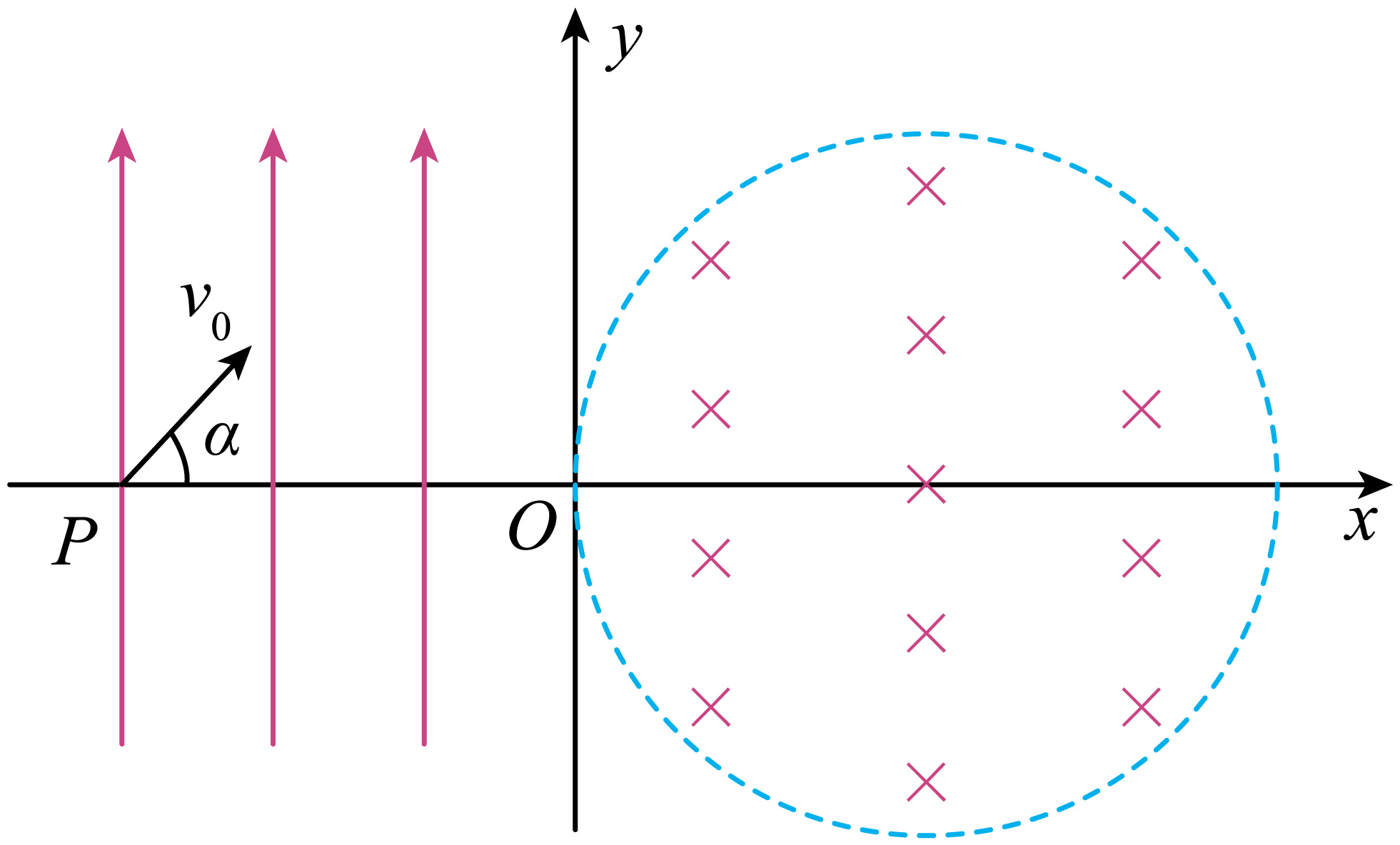
粒子经过$y$轴的位置与原点$O$的距离；

$\\dfrac{1}{2}L$

粒子在电场中的运动为类平抛运动的逆运动，水平方向$L=v_{0}\cos \alpha⋅t_{1}$

竖直方向$y=\dfrac{1}{2}v_{0}\sin\alpha \cdot t_{1}$

解得$y=\dfrac{1}{2}L$

电场强度和磁感应强度分别为多大；

$\\dfrac{mv_{0}^{2}}{2qL}$，$\\dfrac{\\sqrt{2}mv_{0}}{2qd}$

粒子在电场中的加速度大小$a= \dfrac{qE}{m}$

竖直分位移$y=\dfrac{1}{2}at_{1}^{2}$

解得电场强度$E=\dfrac{mv_{0}^{2}}{2qL}$

粒子进入磁场后做匀速圆周运动，以沿$y$轴负方向的速度射出磁场，运动轨迹如图所示

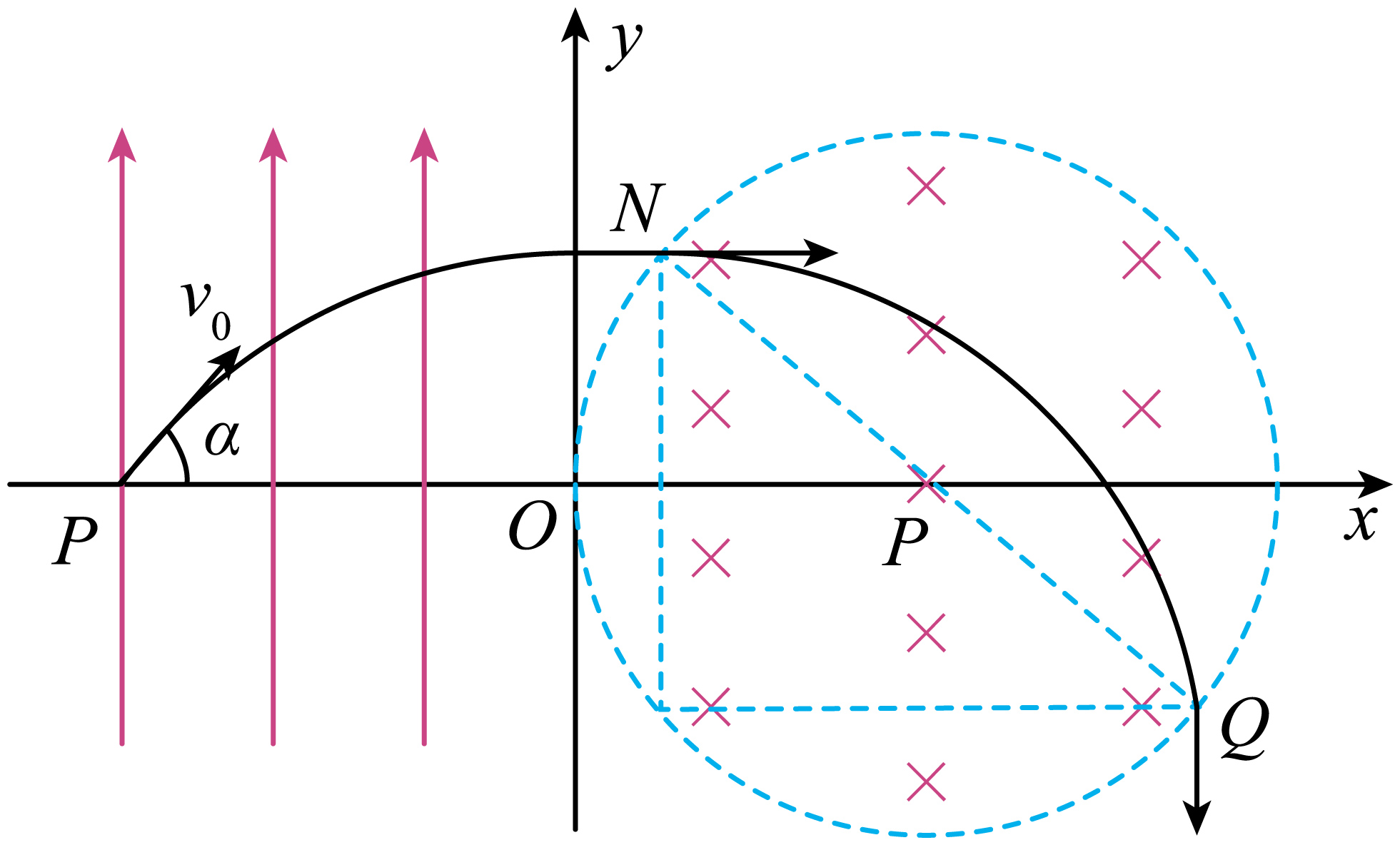
由几何知识可知$NQ$与竖直方向的夹角为$45^\circ $，则$NP=\sqrt{2}y=\dfrac{\sqrt{2}}{2}L$

$NQ$刚好为圆形边界的直径，则粒子在磁场中做圆周运动的轨迹半径$r=L$

粒子在磁场中做圆周运动，由牛顿第二定律有$qvB=m\dfrac{v^{2}}{r}$

粒子的速度$v=v_{0}\cos \alpha$

解得$B=\dfrac{\sqrt{2}mv_{0}}{2qd}$

粒子从出发到离开磁场的总时间。

$\\dfrac{L}{v_{0}}+\\dfrac{\\sqrt{2}(1+ \\pi)L}{2v_{0}}$

粒子在电场中的运动时间$t_{1}= \dfrac{d}{v_{0}\cos\alpha}=\dfrac{\sqrt{2}L}{v_{0}}$

粒子离开电场后进入磁场前做匀速直线运动，位移$x=\dfrac{\sqrt{2}L}{2}-\dfrac{L}{2}$

粒子做直线运动的时间$t_{2}=\dfrac{x}{v}=\dfrac{\left( 2-\sqrt{2} \right)L}{2v_{0}}$

粒子在磁场中做圆周运动的时间$t_{3}=\dfrac{1}{4}\times\dfrac{2\pi r}{v}$

粒子从$M$点出发到穿出磁场所用的总时间$t=t_{1}+t_{2}+t_{3}=\dfrac{L}{v_{0}}+\dfrac{\sqrt{2}(1+\pi)L}{2v_{0}}$