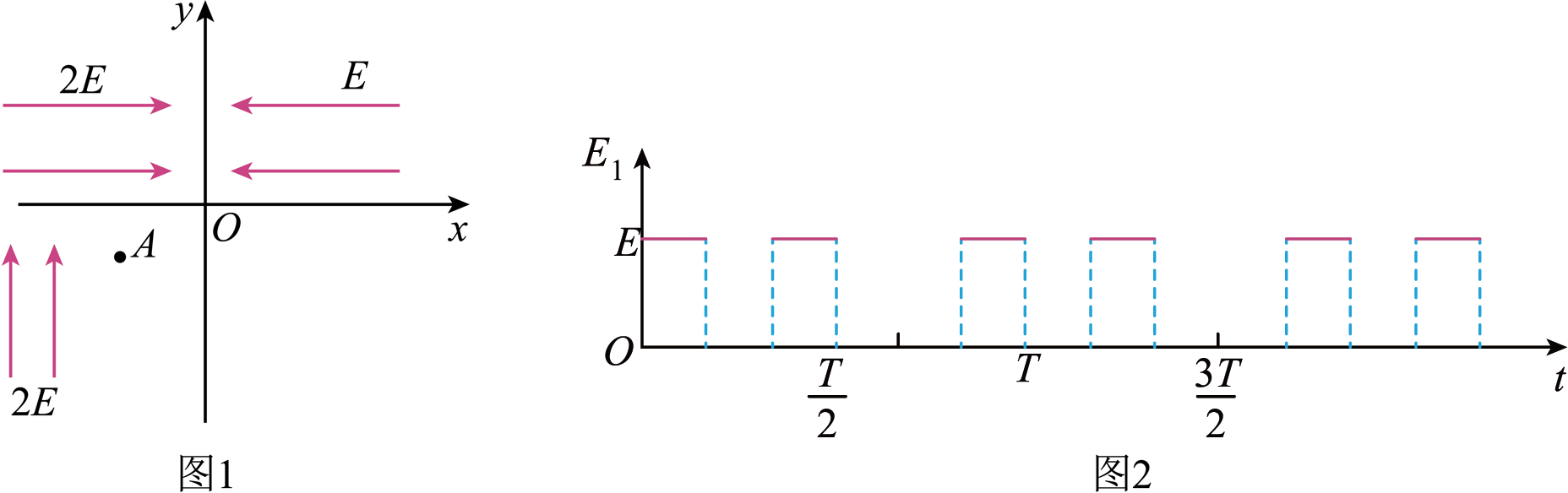
求离子第一次通过 $x$轴时的速度大小；

$2\\sqrt{\\dfrac{Eqd}{m}}$；

离子第一次通过 $x$轴时的速度大小为$v_{1}$，在第三象限的电场中，由动能定理得$2qEd=\dfrac{1}{2}mv_{1}^{2}$

解得$v_{1}=2\sqrt{\dfrac{qEd}{m}}$;

求离子第二次通过 $y$轴时的位置坐标；

$(0, 10d)$；

离子在第二象限做类平抛运动，竖直方向有$y_{1}=v_{1}t_{1}$

水平方向有$d=\dfrac{1}{2} \times \dfrac{2qE}{m}t_{1}^{2}$

联立解得$y_{1}=2d$

$t_{1}=\sqrt{\dfrac{md}{qE}}=\dfrac{1}{12}T$

故离子第一次通过$y$轴时的位置坐标为$(0, 2d)$；

因第一象限电场强度为第二象限的一半，因此第一象限加速度大小为第二象限一半，且方向相反，因此在第一象限内需要用$2t_{1}$时间先匀减速为$0$，再通过$2t_{1}$时间反向匀加速再次回到$y$轴，由此有$t=2t_{1}+2t_{1}=4t_{1}$

竖直方向的速度不受影响，一直是$v_{1}$，因此有$y_{2}=v_{1} \times 4t_{1}=8d$

最后有$y=y_{1}+y_{2}=10d$

离子第二次通过 $y$轴时的位置坐标$(0, 10d)$；

若离子第一次进入第一象限后开始计时，第一象限中的电场按图$2$ 规律变化（图中 $T=12\sqrt{\dfrac{md}{Eq}}$），忽略电场变化引起的电磁感应现象，求离子第$4$ 次通过$y$轴的位置坐标。  

$(0, 38d)$。

由第二问可知，带电粒子第一次经过 $y$ 轴的坐标为$(0, 2d)$，用时为$t_{1}=\sqrt{\dfrac{md}{qE}}=\dfrac{1}{12}T$

此时粒子进入第一象限，在水平方向上，粒子在$0-\dfrac{T}{6}$的时间内减速为 $0$，$\dfrac{T}{6}-\dfrac{T}{3}$的时间内水平速度为 $0$，在$\dfrac{T}{3}-\dfrac{T}{2}$的时间内水平方向匀加速，再次回到$y$轴，总时间为 $6t_{1}$，因此有$y_{2}=v_{1} \times 6t_{1}=2\sqrt{\dfrac{qEd}{m}} \times 6\sqrt{\dfrac{md}{qE}}=12d$

此时粒子离开第一象限进入第二象限，此时时刻为$\dfrac{1}{2}T$。进入第二象限后，水平方向，经过$\dfrac{1}{12}T$的时间先匀减速为 $0$，再次反向匀加速$\dfrac{1}{12}T$时间回到$y$轴。因此有$y_{3}=v_{1} \times 2t_{1}=2\sqrt{\dfrac{qEd}{m}} \times 2\sqrt{\dfrac{md}{qE}}=4d$

此时粒子与第三次经过$y$轴，此时时刻为$\dfrac{2}{3}T$。

在$\dfrac{2T}{3}-\dfrac{5T}{6}$，由于此时第一象限内不存在电场，带电粒子在水平方向上匀速向右。

在$\dfrac{5T}{6}-T$时间内出现电场，带电粒子匀减速为 $0$。

在$T-\dfrac{7T}{6}$的时间内，第一象限不存在电场，同时粒子在水平方向的速度也为 $0$，在水平方向不运动。

在$\dfrac{7T}{6}-\dfrac{4}{3}T$的时间内，带电粒子受到向左的电场力，向左匀加速，和匀减速的位移相互抵消。

在$\dfrac{4}{3}T-\dfrac{9T}{6}$的时间内，第一象限不存在电场，带电粒子再次在水平方向上做匀速运动，与$\dfrac{2T}{3}-\dfrac{5T}{6}$时间内的位移相互抵消，再次回到$y$轴。

此时粒子第四次回到$y$轴，此次用时总时间为$\dfrac{5}{6}T=10t_{1}$

因此有$y_{4}=v_{1} \times 10t_{1}=20d$

最后有$y=y_{1}+y_{2}+y_{3}+y_{4}=38d$

离子第$4$ 次通过$y$轴的位置坐标$(0, 38d)$。