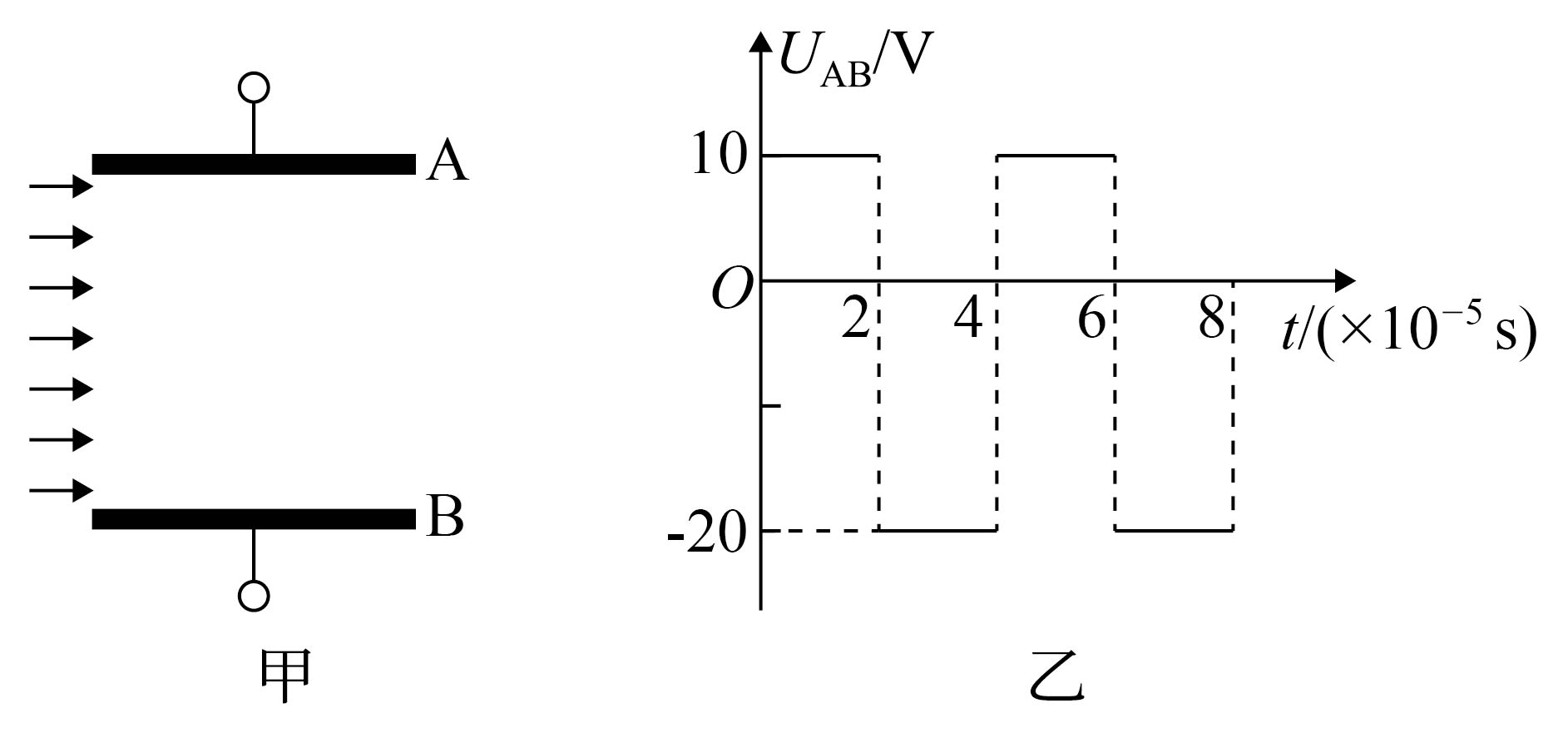
如图甲所示，在水平放置平行金属板$\rm A$、$\rm B$左侧有一线状粒子发射源（图中未画出），能发出宽度为$d$、速度相同的带正电粒子束。$t=0$时刻该粒子束恰好完全水平进入平行金属板间。已知粒子束的速度$v_{0}=1\times10^{3}\text{ m/s}$，比荷$\dfrac{q}{m}=1\times10^{6}\text{ C/kg}$，两板间距为$d=20\text{ cm}$，板长$L=4\ \text{cm}$，极板间加如图乙所示的交变电压。不考虑电容器的边缘效应，也不考虑击中极板的粒子对板间电压的影响，不计粒子重力和粒子间的相互作用力。则粒子射出电场时的位置到$B$板的距离至少为$(\quad\ \ \ \ )$

$0.0025\\text{ m}$

$0.005\\text{ m}$

$0.01\\text{ m}$

$0.015\\text{ m}$

粒子束在水平方向做匀速直线运动，则其射出电场所需时间为$t=\dfrac{L}{v_{0}}=4\times10^{-5}\text{ s}$

若零时刻射入电场的粒子从靠近$B$板进入电场且能射出电场，$0\sim2\times {{10}^{-5}}\text{s}$时间内，$A$板带正电，$B$板带负电，粒子向下做类平抛运动，粒子的加速度大小为${{a}_{1}}=\dfrac{q{{E}_{1}}}{m}=\dfrac{q{{U}_{1}}}{md}=5\times {{10}^{7}}\text{m/}{{\text{s}}^{2}}$

竖直方向的位移为${{y}_{1}}=\dfrac{1}{2}{{a}_{1}}t_{1}^{2}=0.01\text{m}$

$2\times10^{-5}\sim4\times10^{-5}\text{s}$时间内，$A$板带负电，$B$板带正电，粒子向下做类斜抛运动，粒子的加速度大小为${{a}_{2}}=\dfrac{q{{E}_{2}}}{m}=\dfrac{q{{U}_{2}}}{md}=1\times {{10}^{8}}\text{m/}{{\text{s}}^{2}}$

第一段类平抛运动的末速度和第二段类斜抛运动的初速度相同，第二段竖直方向做减速运动，则有${{a}_{1}}{{t}_{1}}={{a}_{2}}{{t}_{2}}$，解得$t_{2}=\dfrac{a_{1}}{a_{2}}t_{1}=1\times10^{-5}\text{ s}$

第二段类斜抛运动在竖直方向的位移为$y_{2}=\dfrac{1}{2}a_{2}t_{2}^{2}=0.005\text{ m}$

当类斜抛运动轨迹与$B$板如下图所示相切时，射出电场时粒子到$B$板距离最小，最小距离为$y_{\text{min}}=y_{2}=0.005\text{ m}$

故$\rm B$正确，$\rm ACD$错误。

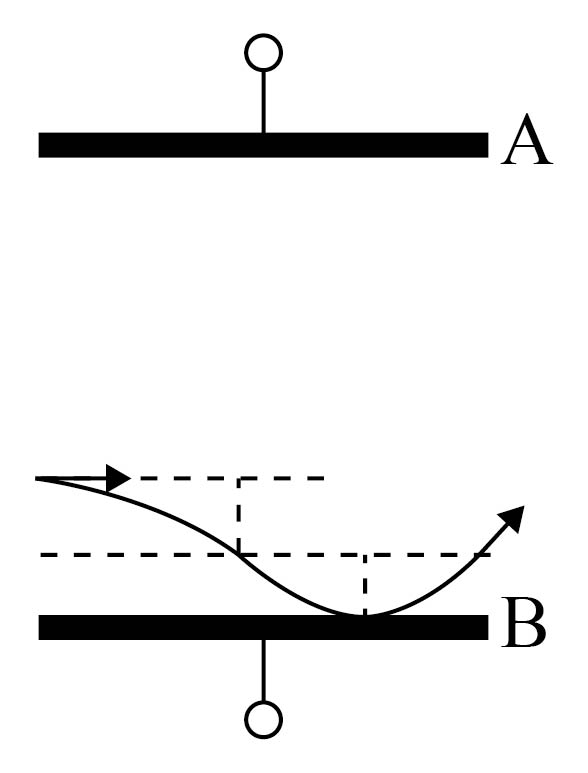
故选$B$。