| 带电粒子在交变电场中的运动 题目答案及解析
稿件来源:高途
| 带电粒子在交变电场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在交变电场中的运动
如图甲所示,$\alpha$粒子射线管由平行于$x$轴的平行金属板$A$、$B$组成,$A$、$B$板长度和板间距均为$L$,$A$、$B$板中间有平行于$x$轴的绝缘细管$C$,开口在$y$轴上。粒子源$P$放置在$A$极板左下端,可以沿特定方向发射$\alpha$粒子。当$A$、$B$板加上某一电压时,$\alpha$粒子刚好能以速度$v$水平进入细管$C$,保持速度不变,再进入静电分析器中做匀速圆周运动,已知静电分析器中电场线的方向均沿半径方向指向圆心$O$,$\alpha$粒子在静电分析器中运动的轨迹半径为$L$。之后$\alpha$粒子垂直$x$轴进入第四象限(此时对应图乙$t=0$时刻),施加如图乙所示沿$x$轴方向的交变电场。规定沿$x$轴正方向为电场正方向。已知$\alpha$粒子电荷量大小为$q$,质量为$m$,重力不计。求:
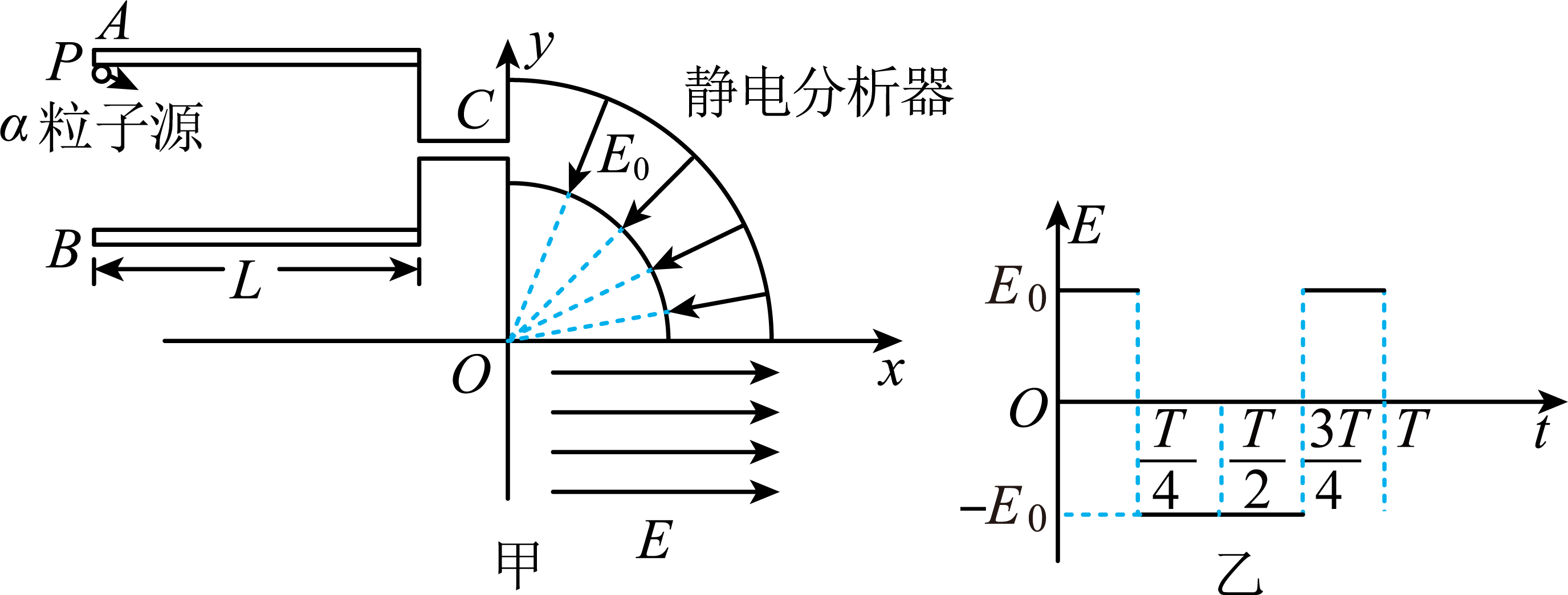
静电分析器中的场强大小$E_{0}$;
$\\dfrac{mv^{2}}{qL}$;
"]]在静电分析器中,由牛顿第二定律有$q \cdot E_{0}=m\dfrac{v^{2}}{r}$
可得$E_{0}=\dfrac{mv^{2}}{qL}$
$\alpha$粒子从粒子源$P$发射时的初速度大小;
$\\sqrt{2}v$;
"]]由题意可知,$\alpha$粒子的运动可以认为反方向的类平抛运动,设运动时间为$t$,则有
水平方向有$L=vt$
竖直方向有$\dfrac{L}{2}=\dfrac{0+v_{y}}{2} \cdot t$
则初速度大小$v_{0}=\sqrt{v^{2}+{v_{y}}^{2}}$
解得$v_{0}=\sqrt{2}v$
当$t=T$时,$\alpha$粒子的坐标。
$(L,-vT)$
"]]$\alpha$粒子进入第四象限做类平抛运动。第一个$\dfrac{T}{4}$内做匀加速直线运动,第二个$\dfrac{T}{4}$内做匀减速直线运动,第三个$\dfrac{T}{4}$内反向匀加速,第四个$\dfrac{T}{4}$内再匀减速。由运动的对称性可知$\alpha$粒子在$x$轴上一个周期内的位移为$0$,在$-y$方向上$\alpha$粒子做匀速直线运动,故$t=T$时,$\alpha$粒子的纵坐标为$y=−vT$
在$t=T$时,$\alpha$粒子的坐标为$(L,-vT)$
| 带电粒子在交变电场中的运动题目答案及解析(完整版)
