| 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
| 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
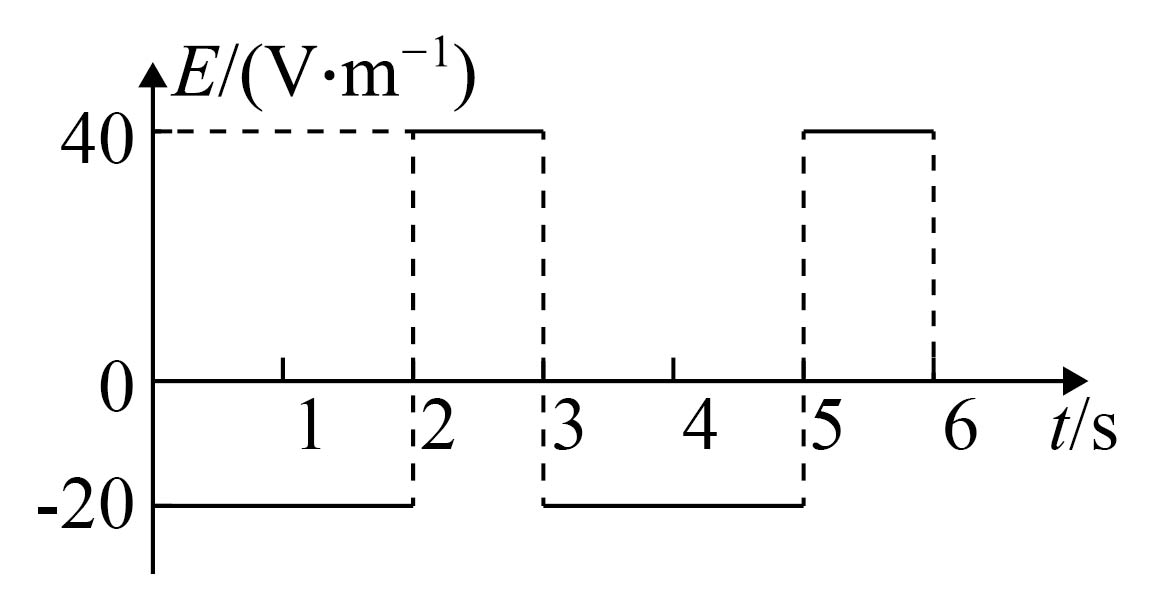
匀强电场的电场强度$E$随时间$t$变化的图像如图所示。当$t=0$时,在此匀强电场中由静止释放一个带正电的粒子,带电粒子只受静电力的作用,下列说法正确的是$(\quad\ \ \ \ )$
带电粒子将做往复运动
","$\\rm 3\\ s$末带电粒子回到原出发点
","$\\rm 3\\ s$末带电粒子的速度不为零
","前$\\rm 3\\ s$内,静电力做的总功为零
"]$\rm ABC$.带电粒子由静止释放后,在$0\sim2\text{ s}$时间内,由牛顿第二定律可知粒子的加速度大小为${{a}_{1}}=\dfrac{qE}{m}$,在$2\text{s}\sim 3\text{s}$时间内,粒子的加速度大小为${{a}_{2}}=\dfrac{2qE}{m}$;
可知粒子由静止先以加速度${{a}_{1}}$加速$\rm 2\ s$,再以加速度${{a}_{2}}$减速$\rm 1\ s$,由于${{a}_{2}}=2{{a}_{1}}$,可知$\rm 3\ s$末粒子速度为零,同理在$3\text{ s}\sim5\text{ s}$时间内由静止又以加速度${{a}_{1}}$加速$\rm 2\ s$,再以加速度${{a}_{2}}$减速$\rm 1\ s$,此时粒子速度是零,因此粒子在$0\sim6\text{ s}$时间内,带电粒子将始终向同一个方向运动,其速度时间图像如图所示,故$\rm ABC$错误;
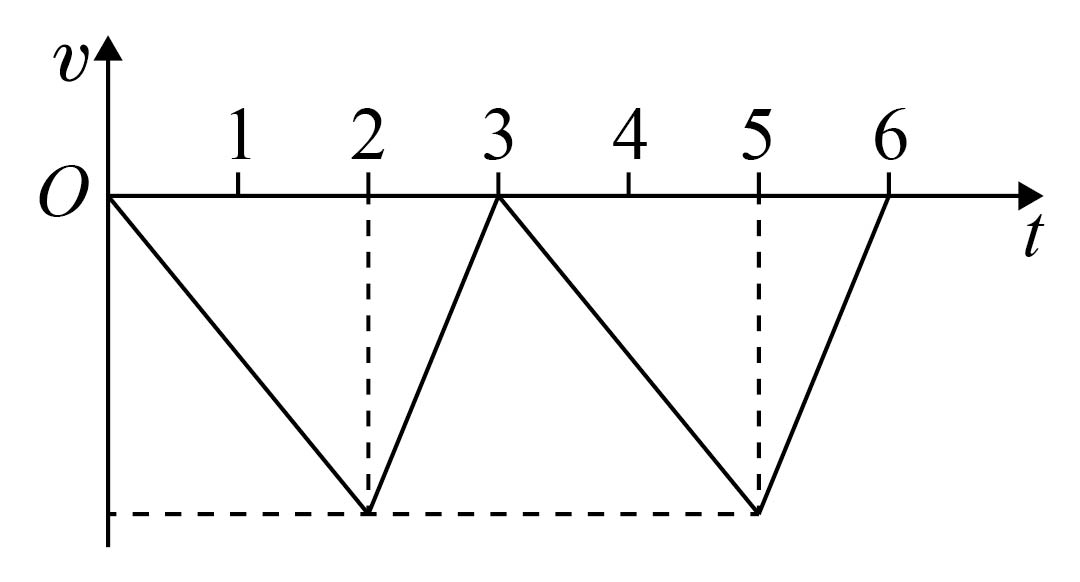
$\rm D$.在前$\rm 3\ s$内,由动能定理可知$W=\text{ }\!\!\Delta\!\!\text{ }{{E}_{\text{k}}}=0-0=0$,故前$\rm 3\ s$内,静电力做的总功是零,$\rm D$正确。
故选$\rm D$。
| 牛顿第二定律的两类基本问题题目答案及解析(完整版)
