以下描述运载火箭升空过程的物理量中，属于矢量的是$(\quad\ \ \ \ )$。

速率

动量

功率

动能

矢量是既有大小又有方向的物理量，动量是矢量，速率、功率、动能都是标量。

故选：$\rm B$。

已知长征五号运载火箭长为$L$，发射初期火箭总质量为$m$，火箭离地上升距离$L$所用的时间为$t$，估算火箭的平均推力$F$。

$F=mg+\\dfrac{2mL}{t^{2}}$

根据牛顿第二定律有$F − mg=ma$，根据位移$—$时间公式有$L= \dfrac{1}{2}at^{2}$，解得$F=mg+\dfrac{2mL}{t^{2}}$

如图所示，当嫦娥六号抵达月球表面某高度时，从椭圆轨道开始进行近月制动，进入环月圆轨道。$a$、$b$为椭圆轨道长轴端点。

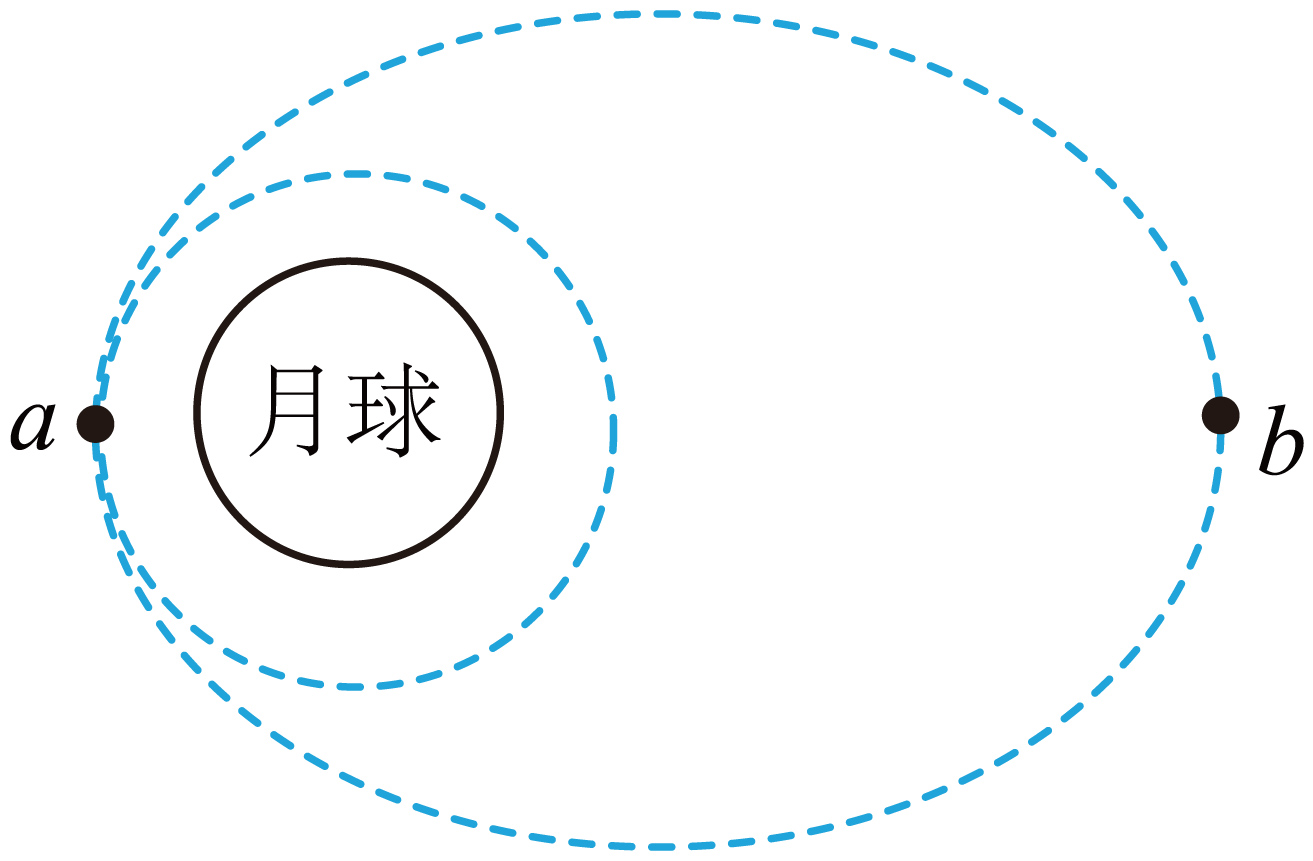
①嫦娥六号在椭圆轨道运行时                 。

$A$．$a$点的速度大于$b$点的速度

$B$．$a$点的速度小于$b$点的速度

$C$．$a$点的加速度大于$b$点的加速度

$D$．$a$点的加速度小于$b$点的加速度

②若嫦娥六号的质量为$m$，在环月圆轨道上的线速度大小为$v$，以无穷远处为零势能面，嫦娥六号的引力势能为                 。

$A$．$mv^{2}$    $B$．$-mv^{2}$    $C$．$\dfrac{1}{2}$$mv^{2}$   $D$．$-$$\dfrac{1}{2}$$mv^{2}$

①$\rm AB$．根据开普勒第二定律可知，近月点$a$点的速度大于$b$点的速度，故$A$正确，$B$错误；

$\rm CD$．根据万有引力提供向心力有$\dfrac{GMm}{r^{2}}=ma$，解得$a=\dfrac{GM}{r^{2}}$，则$a$点的加速度大于$b$点的加速度，故$\rm C$正确，$\rm D$错误；

故选：$\rm AC$。

②设嫦娥六号的环月圆轨道的半径为$r$，由万有引力提供向心力得：$\dfrac{GMm}{r^{2}}=m\dfrac{v^{2}}{r}$，以无穷远处为零势能面，嫦娥六号的引力势能为：$E_{\text{p}}=- \dfrac{GM}{r}$，联立可得$E_{p}=−mv^{2}$

故选：$\rm B$。

嫦娥六号距月面约$100$米时，开始避障下降。若嫦娥六号避障下降时沿图中虚线方向做匀减速直线运动，不计月球大气阻力，则其发动机喷出的气体对其作用力可能为$(\qquad)$

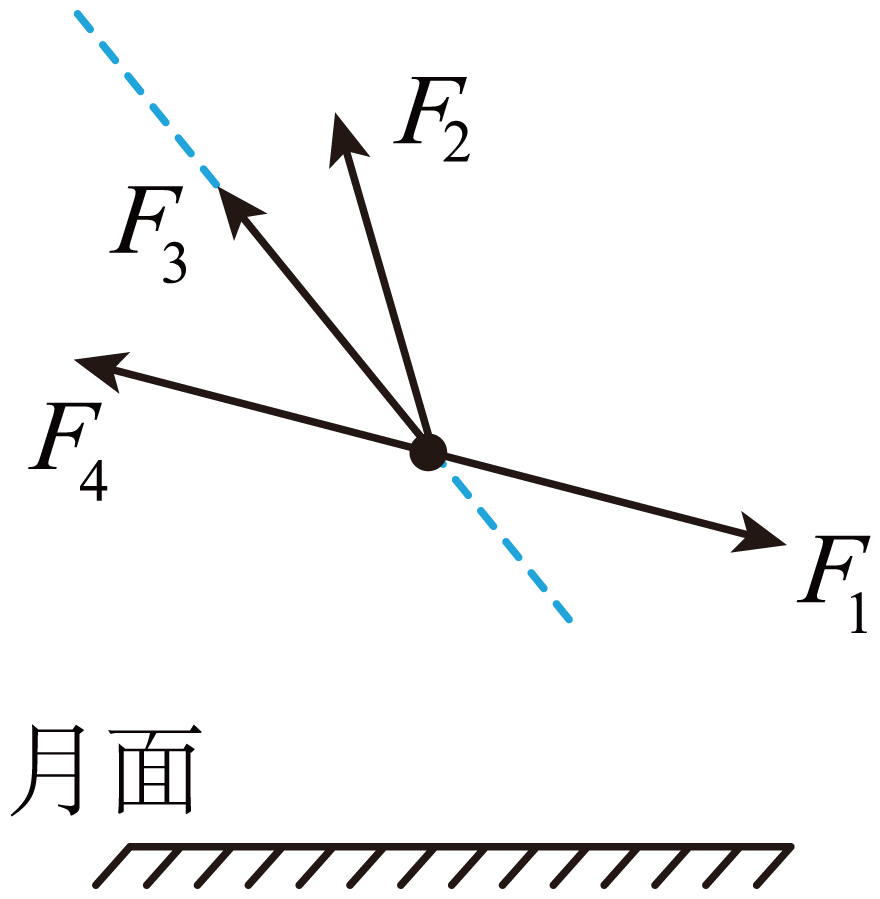
$F_{1}$

$F_{2}$

$F_{3}$

$F_{4}$

如图所示，嫦娥六号沿虚线方向做匀减速直线运动，则喷出的气体对其作用力与重力的合力与运动方向相反。

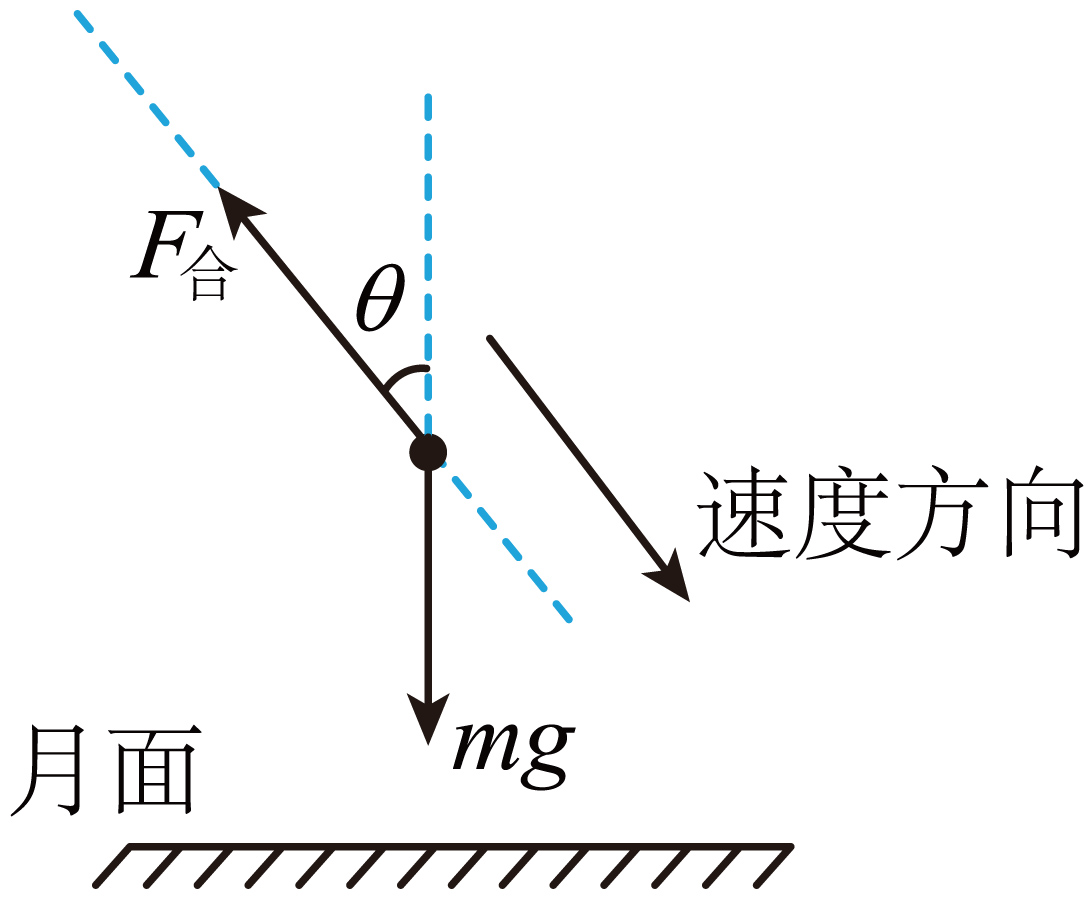
由平行四边形定则，可知发动机喷出的气体对其作用力方向只能在图中的$\theta$角内。

故选：$\rm B$。

嫦娥六号在月球背面南极$-$艾特肯盆地安全着陆。若嫦娥六号的质量为$m$，其四条腿与竖直方向的夹角均为$\theta$，如图所示。月球表面的重力加速度为地球表面重力加速度$g$的$\dfrac{1}{6}$。它静止在月球平坦表面处时，每条腿对月球表面压力的大小为$(\qquad)$

$\\dfrac{mg}{4}$

$\\dfrac{mg}{24}$

$\\dfrac{mg}{4\\cos\\theta}$

$\\dfrac{mg}{6\\cos\\theta}$

嫦娥六号静止在月球平坦表面处时，由平衡条件可知，月球表面对其每条腿的支持力等于其重力的$\dfrac{1}{4}$，根据牛顿第三定律可知，每条腿对月球表面压力的大小等于其重力的$\dfrac{1}{4}$，即$F_{压}=\dfrac{1}{4}m \times \dfrac{1}{6}g= \dfrac{mg}{24}$

故选：$\rm B$。

嫦娥六号携带有月面自主智能移动装置（智能移动相机）。若该装置电动机的最大输出功率为$P$，它在水平月面行驶时受到的阻力大小恒为$F_{f}$。该装置

①在水平月面上行驶的最大速率为                 。

②以恒定功率启动的一段时间内，加速度大小                 。

$A$．先增大后减小    $B$．先减小后增大

$C$．不断增大    $D$．不断减小

①该装置的牵引力与阻力大小相等时，其在水平月面上行驶的速率最大，最大速率为$v_{\text{m}}=\dfrac{P}{F_{\text{f}}}$

②根据牛顿第二定律得$F − F_{f}=ma$，功率$P=Fv$，联立可得$\dfrac{P}{v}-F_{\text{f}}=ma$，以恒定功率启动的一段时间内，$v$逐渐增大，则加速度不断减小，直到减小到零。

故选：$\rm D$。