如图甲所示，$A$、$B$两极板与交变电源相连，交变电源两极间电势差的变化规律如图乙所示，$A$ 板的电势为$0$，质量为$m$，电荷量为$-q$的电子仅在电场力作用下，在 $t=\dfrac{T}{4}$时刻从 $A$ 板的小孔处由静止释放进入两极板间运动，恰好能到达$B$板，则$(\qquad)$

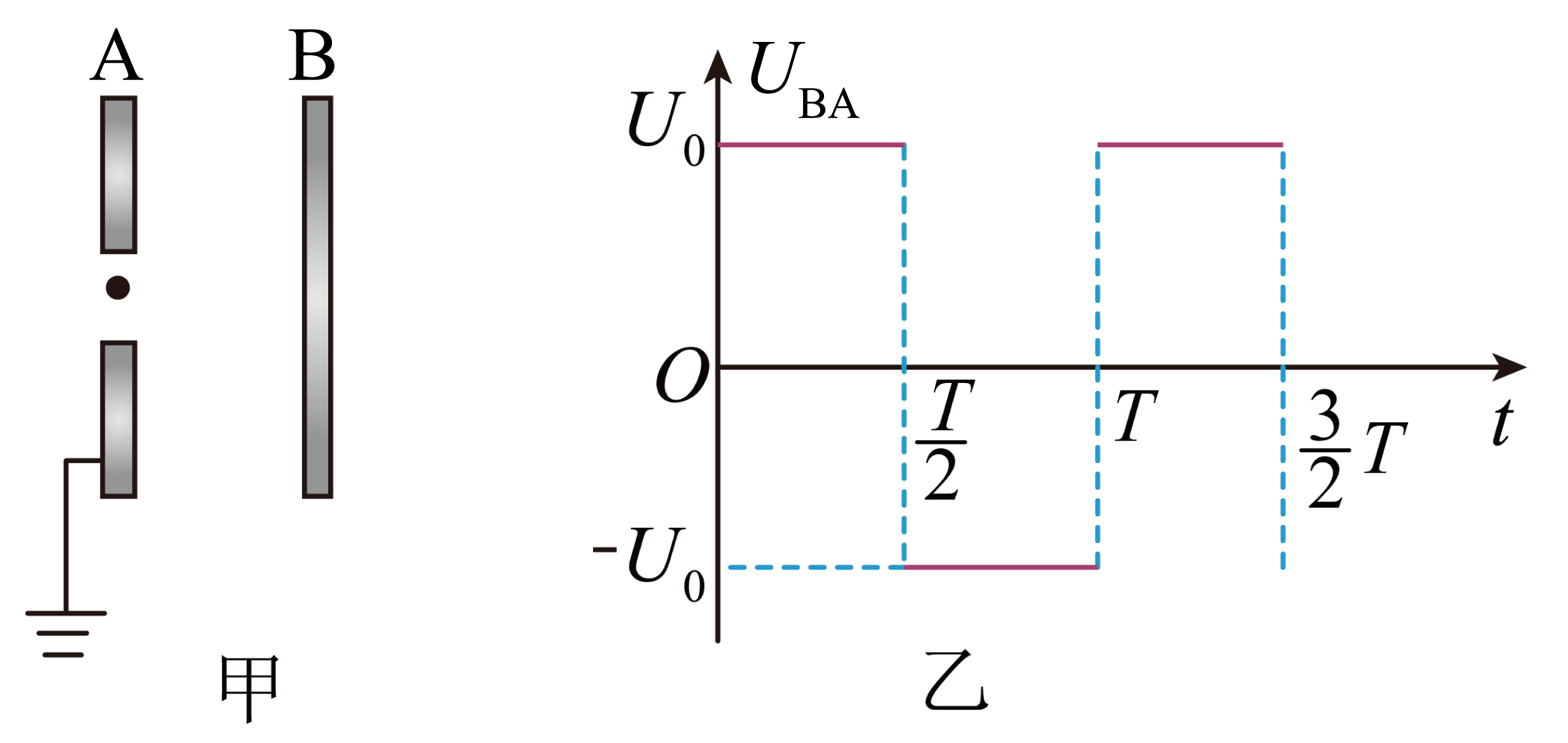
电子在两极板间的最大速度为 $\\sqrt{\\dfrac{2qU_{0}}{m}}$

两极板间的距离为 $\\sqrt{\\dfrac{qU_{0}T^{2}}{16m}}$

若将$B$ 极板向上移动少许，则电子到达 $B$ 板时速度大于$0$

若电子在$t=\\dfrac{T}{8}$时刻进入两极板，它将一直加速向$B$极板运动，最终到达$B$极板

$\rm AB$．电子在$\dfrac{T}{4}$时刻由静止释放进入两极板间运动，前$\dfrac{T}{4}$先匀加速后再匀减速$\dfrac{T}{4}$，在$\dfrac{3T}{4}$时刻恰好到达$B$ 板，设两极板间距为$d$，由牛顿第二定律得到$a=\dfrac{qU_{0}}{md}$，$d=2 \times \dfrac{1}{2}a{\left(\dfrac{T}{4}\right)}^{2}$

解得两极板间距为$d=\sqrt{\dfrac{qU_{0}T^{2}}{16m}}$

由题意可知，运动$\dfrac{T}{4}$后，电场反向，此时，速度达到最大值，由运动学可知，最大速度为$v_{\text{m}}=a \cdot \dfrac{T}{4}=\sqrt{\dfrac{qU_{0}}{m}}$

$\rm A$错误，$\rm B$正确；

$\rm C$．若将$B$ 极板向上移动少许，极板间电场强度$E=\dfrac{U_{0}}{d}$不变，电子受力不变，板间距不变，故电子的运动状态不变，仍是$\dfrac{T}{4}\sim\dfrac{T}{2}$时间内做匀加速直线运动，$\dfrac{T}{2}\sim\dfrac{3T}{4}$时间内继续向右做匀减速直线运动，恰好到达$B$ 极板，$\rm C$错误；

$\rm D$．若电子在$\dfrac{T}{8}$时刻进入两极板，则在$\dfrac{T}{8}\sim\dfrac{T}{2}$时间内电子做匀加速直线运动，由运动学知识可知位移为$x=\dfrac{1}{2} \cdot \dfrac{qU_{0}}{md} \cdot {\left(\dfrac{3}{8}T\right)}^{2}=\dfrac{9}{8}d \gt d$

说明电子会一直向$B$板加速运动并打在$B$板上，不会向$A$板运动，$\rm D$正确。

故选：$\rm BD$。