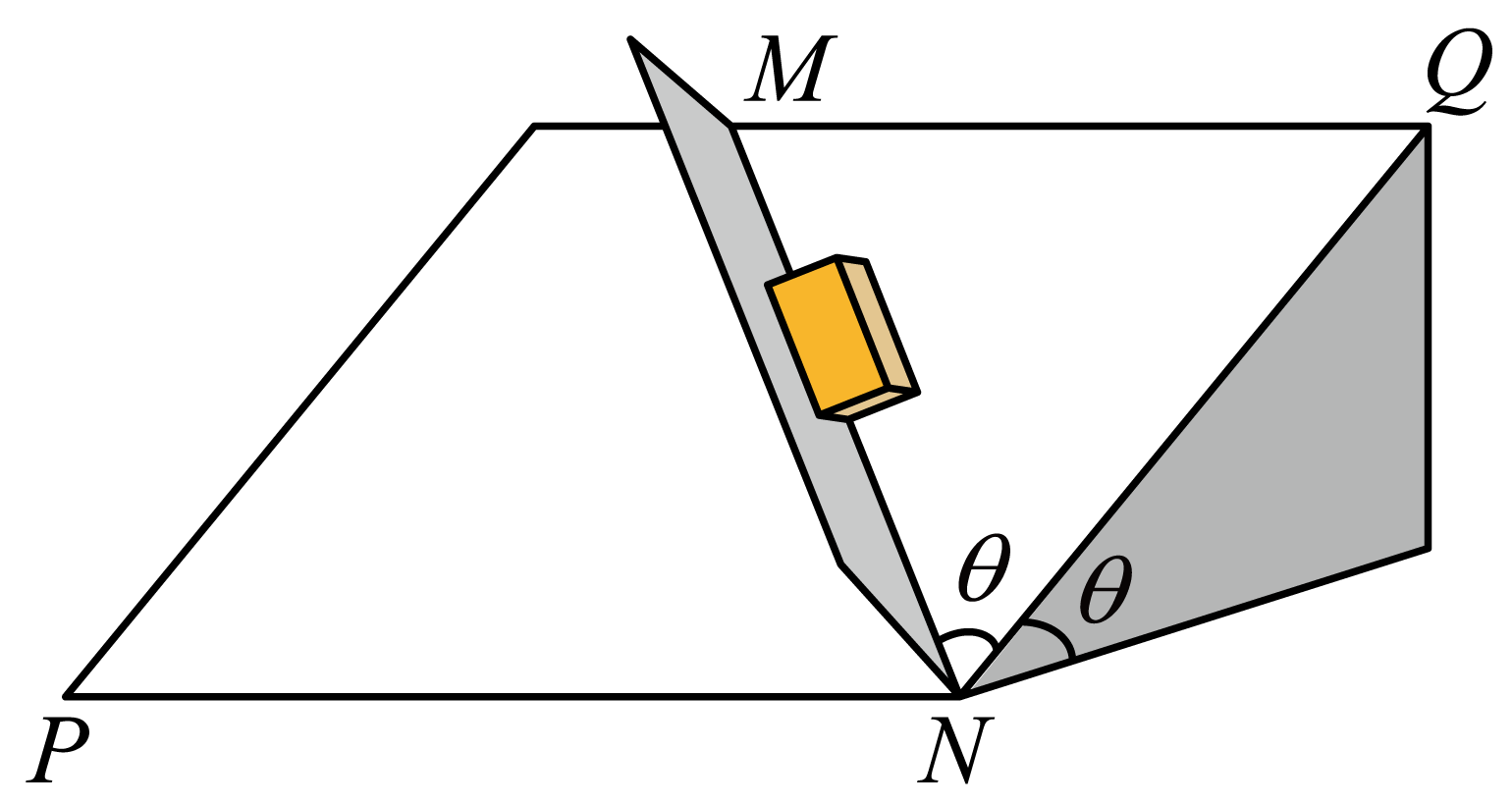
工人在河堤的硬质坡面上固定一垂直坡面的挡板，向坡底运送长方体建筑材料。如图所示，坡面与水平面夹角为$\theta$，交线为$PN$，坡面内$QN$与$PN$垂直，挡板平面与坡面的交线为$MN$，$∠MNQ=\theta$。若建筑材料与坡面、挡板间的动摩擦因数均为$\mu $，重力加速度大小为$g$，则建筑材料沿$MN$向下匀加速滑行的加速度大小为$(\qquad)$

$g\\sin^{2}\\theta − \\mu g\\cos \\theta − \\mu g\\sin \\theta\\cos \\theta$

$g\\sin \\theta\\cos \\theta − \\mu g\\cos \\theta − \\mu g\\sin^{2}\\theta$

$g\\sin \\theta\\cos \\theta − \\mu g\\cos \\theta − \\mu g\\sin \\theta\\cos \\theta$

$g\\cos^{2}\\theta − \\mu g\\cos \\theta − \\mu g\\sin^{2}\\theta$

根据牛顿第二定律$mg\sin \theta\cos \theta − \mu mg\cos \theta − \mu mg\sin \theta\sin \theta=ma$

可得$a=g\sin \theta\cos \theta − \mu g\cos \theta − \mu g\sin^{2}\theta$。

故选：$\rm B$。