一定质量的理想气体经等压过程从状态$a$变化到状态$b$、再经等容过程从状态$b$变化到状态$c$，最后经等温过程从状态$c$回到状态$a$。其压强$p$与体积$V$的关系如图所示。已知$a→b$过程外界对气体做功大小为$W$，气体内能改变$\Delta U$（$W$、$\Delta U$均为绝对值），则$(\qquad)$

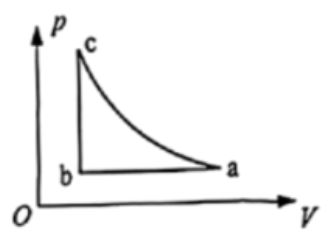
$b→c$过程，气体对外做功为$W$

$b→c$过程，气体内能增加$\\Delta U$

$c→a$过程，气体对外做功为$W$

$c→a$过程，气体内能增加$\\Delta U$

$\rm A$．在$b$到$c$过程中，气体体积不变，外界不对气体做功，气体也不对外界做功，故$\rm A$错误；

$\rm B$．从状态$c$回到状态$a$过程发生的是等温变化，则内能不变，在$b$到$c$过程中，气体体积不变，外界不对气体做功，气体也不对外界做功，压强增大，温度升高，内能增加，且内能增加量等于$a$到$b$过程中内能减少量，故$\rm B$正确；

$\rm C$．在$c$到$a$过程中，气体体积增大，气体对外界做功，做功的多少等于$p-V$图像所围成的面积，可知$c$到$a$过程中气体对外界做功大小大于$a$到$b$过程中外界对气体做功大小，故$\rm C$错误；

$\rm D$．从状态$c$回到状态$a$过程发生的是等温变化，则内能不变，故$\rm D$错误；

故选：$\rm B$；

一体积可变的密闭容器内气体处在某一平衡状态，此时容器内气体压强为$p$。为简化问题，假设气体分子与器壁发生弹性碰撞且方向垂直容器器壁，气体分子平均速率为$v$，每个分子的质量为$m$，则单位时间撞击在容器壁单位面积上的分子数为                 。为减小容器内的压强，可采取的方法有                 和                 ；

假设气体分子与器壁发生弹性碰撞且方向垂直容器器壁，可知碰撞前后速度大小不变，方向相反，以气体分子为研究对象，以分子碰撞器壁时的速度方向为正方向，根据动量定理$−I'=−mv − mv=-2mv$

由牛顿第三定律可知，分子受到的冲量与分子给器壁的冲量大小相等方向相反，所以一个分子与器壁碰撞一次给器壁的冲量为

$I=2mv$

设单位时间撞击在容器壁单位面积上的分子数为$n_{0}$，以器壁的面积$S$为底，在$\Delta t$时间内，碰撞分子总数为$N=n_{0}S\Delta t$

设$N$个分子对面积为$S$的器壁产生的作用力为$F$，$N$个分子对器壁产生的冲量$F\Delta t=NI$

根据压强的定义$p=\dfrac{F}{S}$

解得气体分子对器壁的压强$p=2n_{0}mv$

解得$n_{0}=\dfrac{p}{2mv}$

根据上述解析可知，减小气体压强的办法有减小分子平均动能或者减小分子与容器壁的撞击次数，即降低温度或增大体积；

在实验室中获得温度为$273\;\rm K$、压强为$1.01 \times 10^{-13}\;\rm Pa$的真空，在这样的真空中每立方厘米中的气体分子数约为                 个；

在标准状态（温度为$273\;\rm K$、压强为$1.01 \times 10^{5}\;\rm Pa$）下，气体的摩尔体积为$22.4L$，根据理想气体状态方程$p_{0}V_{0}=n_{0}RT$

解得$R=\dfrac{p_{0}V_{0}}{n_{0}T}$

同理解得该气体每立方厘米中物质的量为$n=\dfrac{pV}{RT}=\dfrac{pVn_{0}}{p_{0}V_{0}}=\dfrac{1.01 \times 10^{- 13} \times 1 \times 10^{- 6} \times 1}{1.01 \times 10^{5} \times 22.4 \times 10^{- 3}}=4.46 \times 10^{- 23}\;\rm{mol}$

每立方厘米中的气体的分子数为$N=nN_{A}=27$；

水龙头流出的水竖直下落，刚从水龙头流出时水流的截面半径为$1.0\;\rm cm$，下落$0.60\rm m$后截面变细，半径为$0.40\;\rm cm$。刚从水龙头流出的水流速度$v_{0}=$                 $\;\rm m/s$。（假设流体不可压缩）

水龙头在单位时间内流出的水的体积（即流量）不变，可知$Q=\dfrac{sv\Delta t}{\Delta t}=sv$

水流下落过程有$\pi r_{0}^{2}v_{0}=\pi r_{1}^{2}v_{1}$

代入数据得$v_{1}=\dfrac{25}{4}v_{0}$

对下落阶段，根据运动学关系有$v_{1}^{2} − v_{0}^{2}=2gh$

解得$v_{0}=\dfrac{8\sqrt{203}}{203}\:\rm {{m/s}}$。