| 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
| 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
利用如图所示的实验装置可以测量滑块与长木板之间的动摩擦因数,一块表面平整的长木板放在水平桌面上,然后把一根弹簧固定在木板左端$O$点。$A$与$O$的距离刚好等于弹簧的自然长度。滑块放在长木板上不与弹簧栓接。
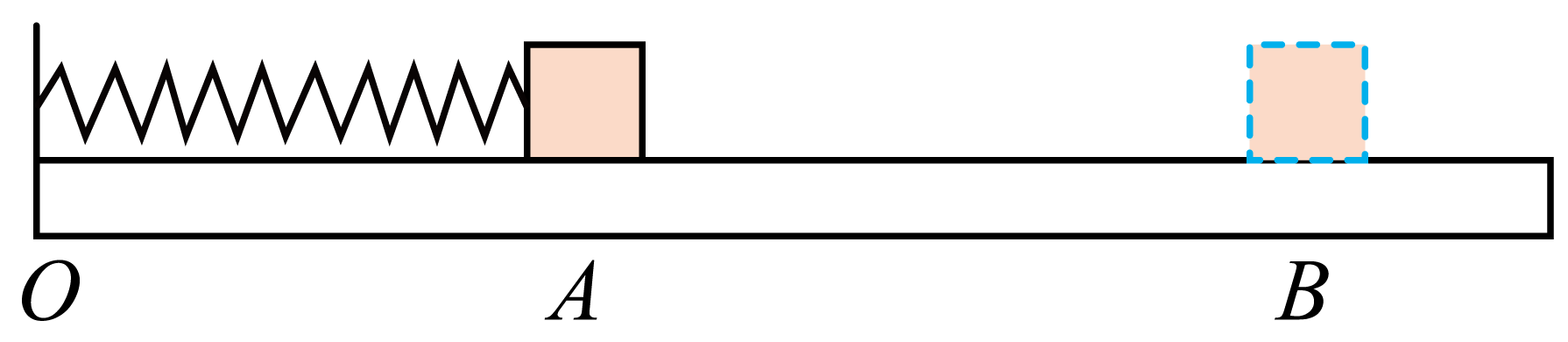
利用手机端秒表功能,可以简易测量滑块与木板之间的动摩擦因数,让滑块压缩弹簧,然后释放滑块,运动到$B$点停下,测得由$A$到$B$的时间为$t$,用直尺测出$A$、$B$之间的距离为$l$,则动摩擦因数测量结果的表达式为$\mu =$ (用$t$、$l$、$g$表示)。
滑块由$A$到$B$,由牛顿第二定律得$a=\dfrac{\mu mg}{m}=\mu g$,根据运动公式$l=\dfrac{1}{2}a{{t}^{2}}$,解得$\mu =\dfrac{2l}{g{{t}^{2}}}$。
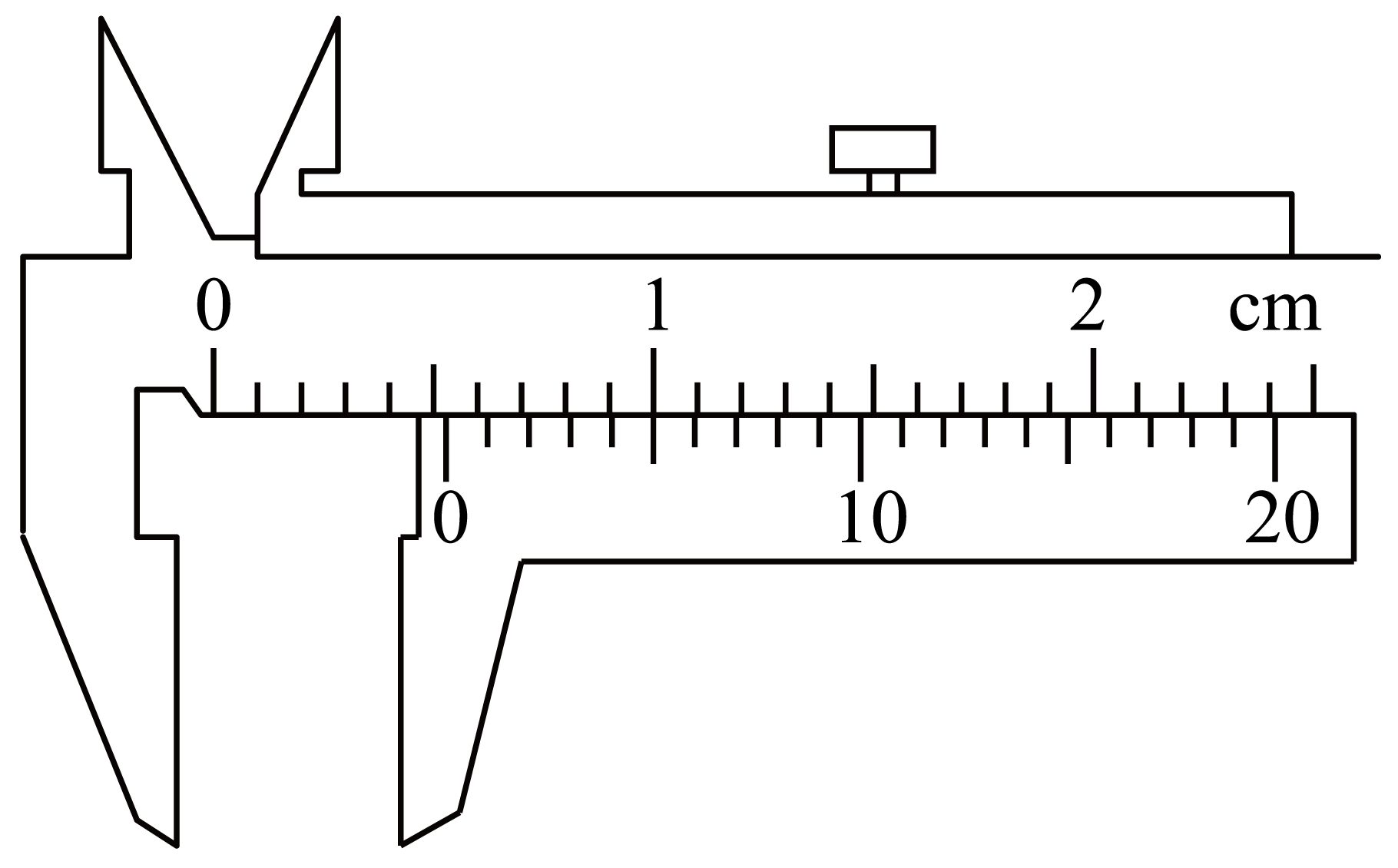
由于滑块滑行时间较短,导致时间$t$测量误差较大,为了更精确测量动摩擦因数,在$A$位置放置一个光电门,同时在滑块上安装上遮光片,用$20$分度的游标卡尺量测遮光片宽度$d$,结果如图所示,则$d=$ $\rm mm$。
游标卡尺为$20$分度,精度为$\rm 0.05\ mm$,游标尺上$0$刻度线在主尺第$5$条刻度线右侧,游标尺上第$5$条刻度线与主尺刻度线基本重合,所以游标卡尺读数为$\rm 5\ mm+5\times0.05\ mm=5.25\ mm$。
手推滑块压缩弹簧,然后释放滑块,记录下滑块通过光电门时挡光时间为$\Delta t$,测量出滑块停下的位置$B$到$A$的距离$l$;改变弹簧的压缩量,记录下多组$\Delta t$,$l$数据,然后用图像法处理数据,做出$l-\dfrac{1}{\Delta {{t}^{2}}}$图像,如图所示,发现图像是一条直线,在直线上取两点$P$、$Q$,测出两点坐标$P\left( x_{1},y_{1}\right)$,$Q\left( x_{2},y_{2}\right)$则滑块与长木板之间的动摩擦因数为$\mu =$ (用$d$,$g$,$x_{1}$,$y_{1}$,$x_{2}$,$y_{2}$,$d$表示)。
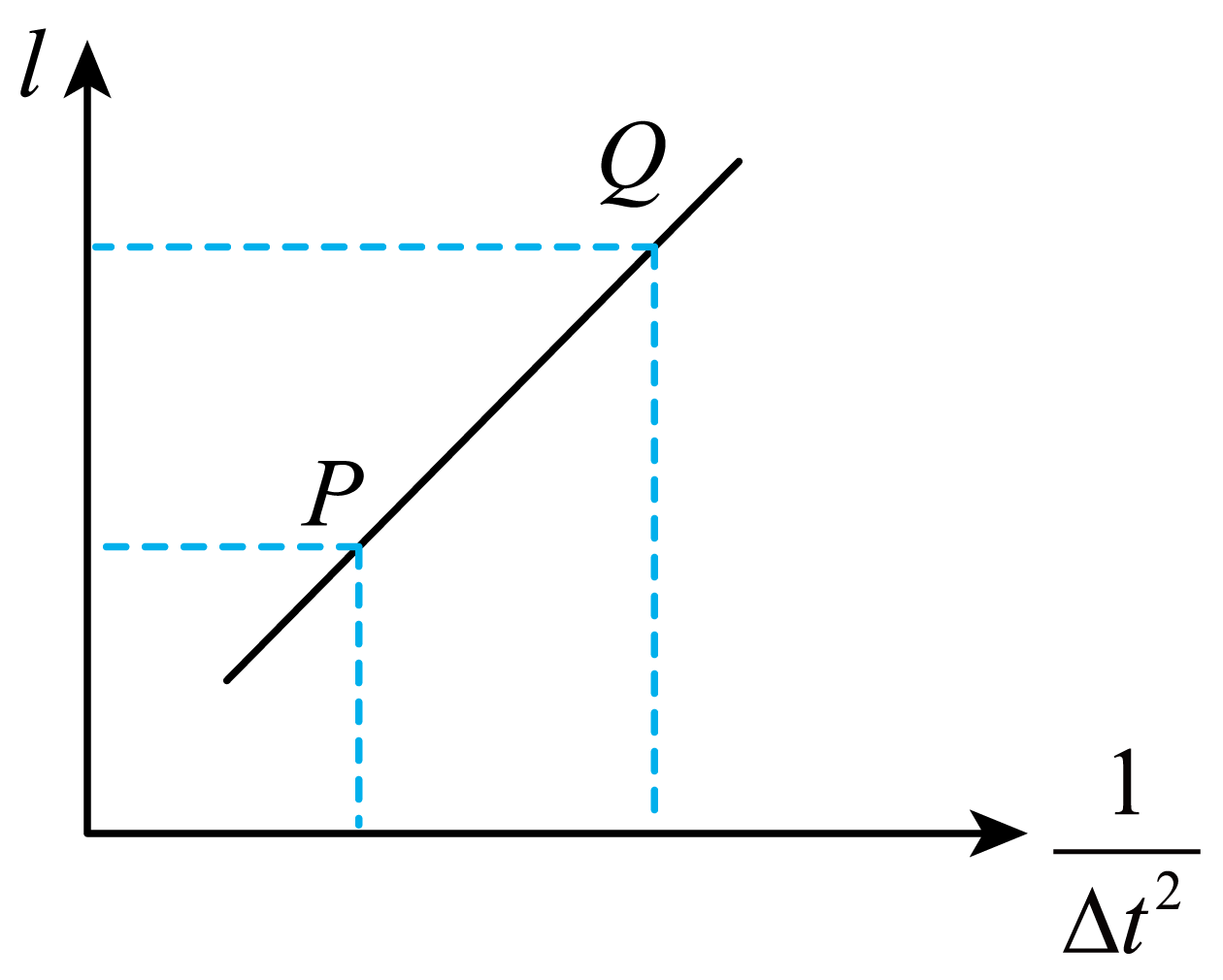
滑块从光电门到停止运动,由牛顿第二定律得$\mu mg=ma$,由匀变速直线运动速度和位移的关系得${{v}^{2}}=2al$,$v=\dfrac{d}{\Delta t}$,解得$l=\dfrac{{{d}^{2}}}{2\mu g}\times \dfrac{1}{\Delta {{t}^{2}}}$,图像斜率$k=\dfrac{{{d}^{2}}}{2\mu g}$,因为$k=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$,解得$\mu=\dfrac{d^{2}\left( x_{2}-x_{1}\right)}{2g\left( y_{2}-y_{1}\right)}$。
| 匀变速直线运动的速度位移公式题目答案及解析(完整版)
