| 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
| 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
图甲为某智能分装系统工作原理示意图,每个散货经倾斜传送带由底端$A$运动到顶端$B$后水平抛出,撞击冲量式传感器使其输出一个脉冲信号,随后竖直掉入以与水平传送带共速度的货箱中,此系统利用传感器探测散货的质量,自动调节水平传送带的速度,实现按规格分装。倾斜传送带与水平地面夹角为$30^\circ $,以速度$v_{0}$匀速运行。若以相同的时间间隔$\Delta t$将散货以几乎为$0$的速度放置在倾斜传送带底端$A$,从放置某个散货时开始计数,当放置第$10$个散货时,第$1$个散货恰好被水平抛出。散货与倾斜传送带间的动摩擦因数$\mu=\dfrac{\sqrt{3}}{2}$,到达顶端前已与传送带共速。设散货与传感器撞击时间极短,撞击后竖直方向速度不变,水平速度变为$0$。每个长度为$d$的货箱装总质为$M$的一批散货。若货箱之间无间隔,重力加速度为$g$。分装系统稳定运行后,连续装货,某段时间传感器输出的每个脉冲信号与横轴所围面积为$I$如图乙,求这段时间内:
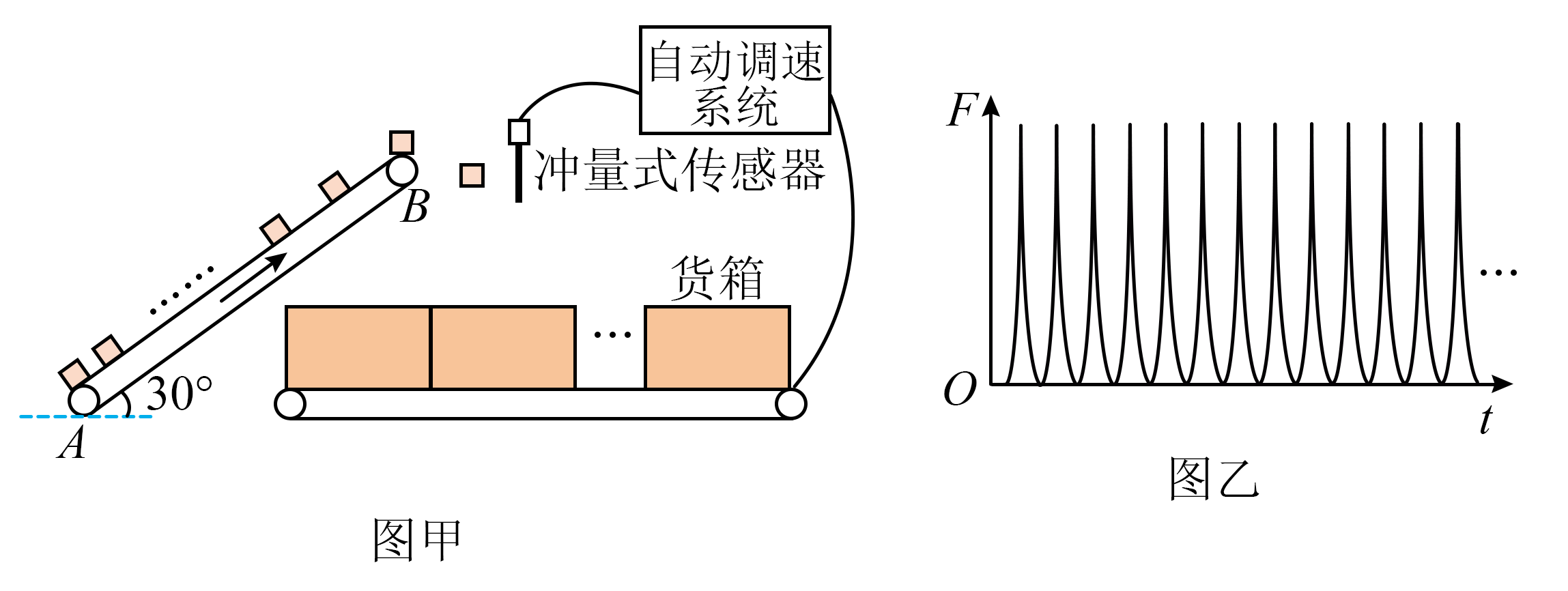
单个散货的质量。
$\\dfrac{I}{v_{0}}$
"]]对单个散货水平方向由动量定理$−I=0-mv_{0}$
解得单个散货的质量为$m=\dfrac{I}{v_{0}}$
水平传送带的平均传送速度大小。
$\\dfrac{dI}{Mv_{0}\\Delta t}$
"]]落入货箱中散货的个数为$N=\dfrac{M}{m} =\dfrac{Mv_{0}}{I}$
则水平传送带的平均传送速度大小为$\overline{v}=\dfrac{d}{N\Delta t}=\dfrac{dI}{Mv_{0}\Delta t}$
倾斜传送带的平均输出功率。
$\\dfrac{I(9g\\Delta t+2v_{0})}{2\\Delta t}$
"]]设倾斜传送带的长度为$L$,其中散货在加速阶段,由牛顿第二定律$\mu mg\cos 30^\circ-mg\sin 30^\circ =ma$
解得$a=\dfrac{1}{4}g$
加速时间$t_{1}=\dfrac{v_{0}}{a}=\dfrac{4v_{0}}{g}$
加速位移$x_{1}=\dfrac{1}{2}at_{1}^{2}=\dfrac{2v_{0}^{2}}{g}$
设匀速时间为$t_{2}$,其中$t_{1}+t_{2}=9\Delta t$
则匀速位移为$x_{2}=v_{0}t_{2}=v_{0}\left(9\Delta t-\dfrac{4v_{0}}{g}\right)$
故传送带的长度为$L=x_{1}+x_{2}=9v_{0}\Delta t-\dfrac{2v_{0}^{2}}{g}$
加速阶段散货与传送带发生的相对位移为$\Delta x=v_{0}t_{1}-x_{1}=\dfrac{2v_{0}^{2}}{g}$
在$\Delta t$时间内传送带额外多做的功为$W=\dfrac{1}{2}mv_{0}^{2}+mgL\sin 30{^\circ}+Q$
其中$m=\dfrac{I}{v_{0}}$,$Q=\mu mg\cos 30^\circ \Delta x$,$\overline{P}=\dfrac{W}{\Delta t}$
联立可得倾斜传送带的平均输出功率为$\overline{P}=\dfrac{I(9g\Delta t+2v_{0})}{2\Delta t}$
| 匀变速直线运动的速度位移公式题目答案及解析(完整版)
