| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
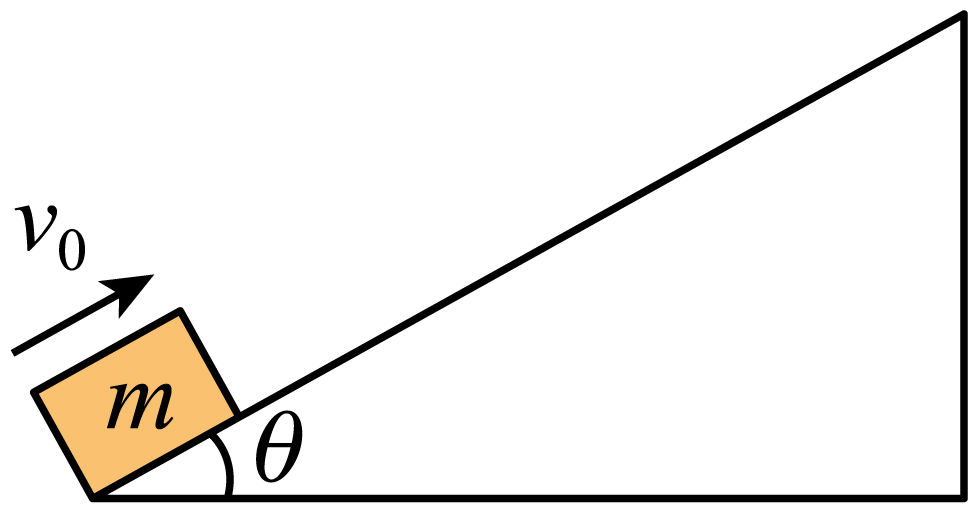
如图所示,质量$m=1\;\rm kg$的滑块以$v_{0}=16\;\rm m/s$的初速度沿倾角为$\theta$(未知)的足够长斜面上滑,滑块与斜面间的动摩擦因数为$\mu $(未知)。滑块向上滑行位移$x=16m$后到达最高点,随即下滑,返回到出发点时的速度为$v=8\;\rm m/s$,重力加速度$g$取$10\;\rm m/s^{2}$,不计空气阻力。求:
滑块上滑过程的加速度$a_{1}$;
$8\\;\\rm m/s^{2}$,方向沿斜面向下;
"]]滑块向上做匀减速直线运动,以沿斜面方向为正方向$0 − v_{0}^{2}=2a_{1}x$
解得$a_{1}=-8\;\rm m/s^{2}$
即加速度大小为$8\;\rm m/s^{2}$,方向沿斜面向下;
滑块下滑过程所用的时间$t$;
$4\\;\\rm s$;
"]]下滑过程,滑块做匀加速直线运动,根据运动学方程$\overline{v}=\dfrac{v}{2}= 4\;\rm \text{m}/\text{s}$
又$x=\overline{v} \cdot t$得$t=4\;\rm s$
斜面的倾角$\theta$以及滑块与斜面间的动摩擦因数为$\mu $。
$30^\\circ $,$\\dfrac{\\sqrt{3}}{5}$
"]]下滑过程,滑块做匀加速直线运动,根据运动学方程$v^{2}=2a_{2}x$
解得$a_{2}=2\;\rm m/s^{2}$
上、下滑过程,根据牛顿第二定律$−(mg\sin \theta+\mu mg\cos \theta)=ma_{1}$
$mg\sin \theta − \mu mg\cos \theta=ma_{2}$
联立可得$\theta=30^\circ $,$\mu=\dfrac{\sqrt{3}}{5}$
| 斜面问题题目答案及解析(完整版)
